Найти момент инерции окружности относительно ее диаметра

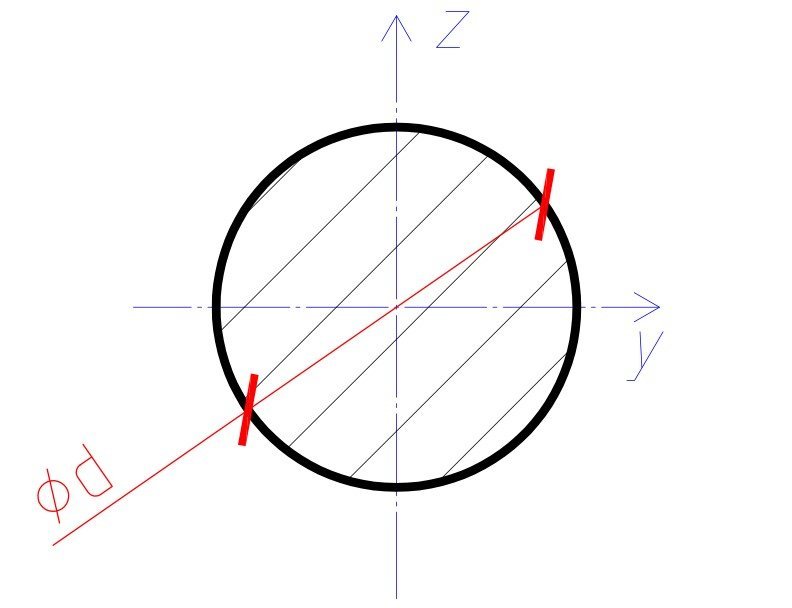
Момент инерции сечения — это сумма произведений элементарных площадок данного сечения на квадраты их расстояний от рассматриваемой оси.

Формула расчета моментов инерции круглого сечения:

D — диаметр круга в см.

Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.

На этой странице представлен самый простой онлайн калькулятор расчета момента инерции круглого сечения в зависимости от размеров. С помощью этого калькулятора вы в один клик сможете рассчитать момент осевой инерции круглого сечения.

Видео:Расчёт момента инерции тела относительно оси вращения. Момент инерции однородного стержняСкачать

Строительный клуб

d — диаметр сечения круга в мм; y, z — центральные оси сечения.

Введите диаметр сечения d в мм:

В результате момент инерции относительно центральных осей y и z равны I_y = I _z =

Видео:Момент инерцииСкачать

Как найти момент инерции круга?

Момент инерции круга относительно центральной оси z равен моменту инерции относительно центральной оси y и рассчитывается по формуле:

l_y = l_z = Π . d 4 /64 ,

l_y — момент инерции относительно центральной оси y в мм 4 ;

l_z — момент инерции относительно центральной оси z в мм 4 ;

d — диаметр круга в мм.

Видео:Урок 94. Вычисление моментов инерции телСкачать

5.I. Вычисление статических моментов и моментов инерции

Предварительно изучите по учебнику Г. М. Фихтенгольца главу XII, п° 206, 207. Рассмотрите внимательно примеры, приведенные в указанных пунктах.

573. Найти статический момент полуокружности относительно диаметра.

Решение. Выберем систему координат так, чтобы центр окружности совпадал с началом координат, а диаметр, относительно которого мы ищем сгатический момент, совпадал с осью Ох. Тогда статический момент полуокружности относительно диаметра выразится следующей формулой:

В выбранной системе координат уравнение полуокружности запишется так: у —V R2—х. Тогда

574. Найти статические моменты относительно осей Ox и Oy дуги эллипса , расположен

ной в первом квадранте.

Решение. Найдем статический момент дуги эллипса относительно оси Ох. Из уравнения эллипса имеем

(мы берем перед корнем знак , так как по условию кривая расположена в первом квадранте).

Найдем статический момент дуги эллипса относительно оси Oy. Из уравнения эллипса имеем:

X = JLyW=T*-, dl = — L YbUg^ZFldy.

К, -|f VF=V? — j — /езщрг dy=

575. Найти статический момент прямоугольника с основанием а и высотой h относительно его сторон.

Решение. Выберем систему координат так, чтобы ось Ox совпадала с основанием, а начало координат — с прилегающей к основанию стороной. Тогда статический момент плоского тела относительно оси Ox будет вычисляться по формуле:

В нашем случае у = h,

Статический момент относительно оси Oy вычисляется по формуле:

576. Налти статический момент фигуры, представленной на рисунке 23 относительно стороны OD1 если известно, что OA = 3 см, AB = 5 см, BC = 5 см, OF = 8см, а дуга CD есть четвертая часть окружности радиуса CF = FD = S см.

Решение. Как видно из рисунка 23, данная фигура имеет сложную форму. Разобьем это тело на простые геометрические фигуры и применим затем теорему: статический момент фигуры относительно некоторой оси равен сумме статических моментов ее частей относительно той же оси.

Выберем систему координат, как показано на рисунке 23. Легко видеть, что данную фигуру можно рассматривать как сумму дзух трапеций OABM и MBCF и одной четвертой части круга.

Координаты точек At Bt C9 Dy F определить легко: Л (0, 3), В (4, 6), С (8, 3), £>(11, 0), F( 8, 0).

Найдем уравнения прямых AB и BCt как уравнения прямых, проходящих через две данные точки:

уравнение прямой AB:

уравнение прямой ВС:

Так как центр F окружности лежит на оси Ox и отстоит от начала координат на расстоянии OF — 8, то уравнение окружности будет

Учитывая все вышеизложенное, найдем:

577. Найти статический момент тела, ограниченного одной аркой циклоиды относительно оси Ох.

Решение. Так как параметр t для одной арки циклоиды изменяется от 0 до 2я, то

578. Найти момент инерции одной арки циклоиды

Относительно оси Ох. Решение. Как было показано в теоретическом курсе, момент инерции дуги относительно оси Ox вычисляется по формуле:

где —дифференциал дуги. Найдем дифференциал дуги:

579. Найти момент инерции дуги окружности

, лежащей в первом квадранте, относительно

Решение. Как известно, момент инерции кривой относительно оси Oy вычисляется по формуле:

Так как и, следо

Для вычисления Была использована

580. Найти момент инерциифигуры, вграниченной дугой полуокружности Относительно

Решение. Как известно из теоретического курса, момент инерции Ix плоского тела относительно оси Ojc равен:

где dS—элементарная площадь тела.

581. Найти статические моменты дуги параболы у2 = 2х (у > 0) относительно осей Ox и Oy от х = 0 до

582. Найти статический момент дуги астроиды х3 —2_ 2_

— j-y 3 = а 3 , лежащей в первом квадранте, относительно оси Oy.

583. Найти статический момент относительно оси Ox

584. Вычислить статический момент фигур, ограниченных следующими линиями:

COS X OT ТОЧКИ X —до точки

дуги косинусоиды у

а) у —- и у = Xi относительно оси Ох

б) у — X1 и у = Y х относительно оси Ох.

585. Вычислить статический момент фигуры, представленной на рисунке 24, где BC\AD, CKJ_AD, AB = 5, BC = 2, CK = KD = 3, AK = 6, относительно оси Ох.

586. Найти статический момент прямоугольного равнобедренного треугольника с катетом, равным а, относительно этого катета.

587. Найти момент инерции отрезка AB, где А (2; 3), В (5; 4), относительно обеих координатных осей.

588. Найти момент инерции треугольника ABC (рис. 25) относительно стороны Ь.

589. Найти момент инерции прямоугольника со сторонами а и b относительно обеих сторон.

590. Найти момент инерции трапеции ABCD относительно ее основания AD1 если AD=а, BC = 6, высота трапеции равна h.

591. Найти момент инерции

параболического сегмента относительно основания. Основание сегмента равно а, «стрела сегмента» равна А.

📽️ Видео

Основы Сопромата. Геометрические характеристики поперечного сеченияСкачать

Момент инерции абсолютно твердого тела. 10 класс.Скачать

Урок 97. Теорема ШтейнераСкачать

Моменты инерции сечения из простых фигурСкачать

5. Момент инерции простейших телСкачать

Геометрические характеристики. Моменты инерции. Радиусы инерции. Сопромат.Скачать

Урок 95. Теорема о взаимно перпендикулярных осяхСкачать

Урок 98. Задачи на вычисление моментов инерции (ч.1)Скачать

Моменты инерции Прямоугольника ► Вывод моментов инерции для прямоугольникаСкачать

Момент инерцииСкачать

Основы сопромата. Задача 4. Момент инерции сложного сеченияСкачать

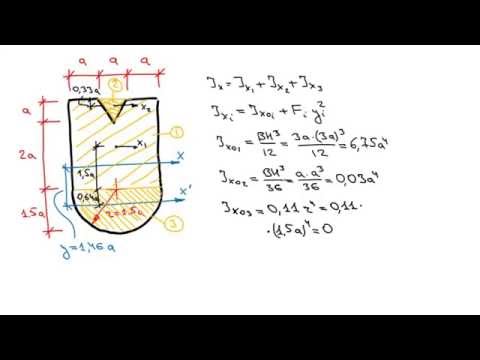
Семинар №6 "Момент инерции. Уравнения моментов" (Чивилев В.И.)Скачать

Физика. 10 класс. Момент инерции абсолютно твердого тела /01.10.2020/Скачать

Определение осевых моментов инерции составного несимметричного сечения. СопроматСкачать

Вычисление моментов инерции составного сеченияСкачать

Момент инерции круга. Моменты инерции простых фигур. #сопроматСкачать

Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать