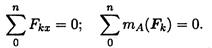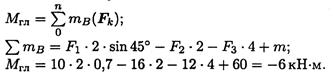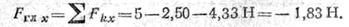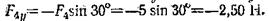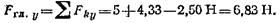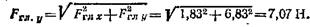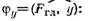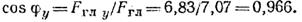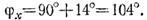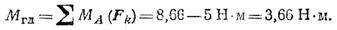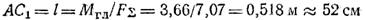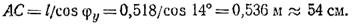2. Плоская система сил.
2.2 Главный вектор и главный момент плоской системы сил.
Приведение к простейшему виду.
2.2.1. Определить главный вектор плоской системы сил, если заданы его проекции на координатные оси Rx = 300Н, Rу = 400Н. (Ответ 500)
2.2.2. Определить главный момент системы двух сил относительно точки А, если силы G = 1Н, F = 5Н, расстояние l = 0,2 м, угол φ = 60°. (Ответ -0,916)
2.2.3. К вершинам квадрата приложены четыре силы F1 = F2 = F3 = F4 = 1Н. Определить модуль равнодействующей этой системы сил. (Ответ 2,0)
2.2.4. За центр приведения данной системы сил выбрана точка, расположенная на оси Оу, в которой главный момент равен нулю. Определить ординату этой точки, если силы
F1 = F2 = F3 = 1Н, F4 = 2Н, радиус r = 1 м. (Ответ -1,0)
2.2.5. К вершинам равностороннего треугольника приложены силы F1 = F2 = F3 = 1Н.
Определить модуль равнодействующей этой системы сил. (Ответ 1,0)
2.2.6. Заданы силы F1 = F2 = F3 = 12H, F4 = 14Н. Определить главный момент заданной плоской системы сил относительно точки О, если радиус r = 0,2 м. (Ответ 0,233)
2.2.7. К вершинам прямоугольного треугольника приложены три силы.
Определить значение угла α в градусах, при котором главный момент данной системы си л
М 0 = -2 кН•м, если сила F2=4 кН, расстояние l = 1 м. (Ответ 30,0)
2.2.8. К вершинам прямоугольного треугольника приложены силы F1 = 3Н, F2 = 6Н, F3 = 14Н. Определить значение угла а в градусах, при котором главный вектор данной системы сил параллелен оси Ох (Ответ 30,0)
2.2.9. К прямоугольнику приложены четыре силы по 10Н каждая. Определить модуль главного вектора заданной системы сил, если угол α = 60°. (Ответ 22,4)
2.2.10. К квадрату приложены шесть сил по 6Н каждая. Определить главный момент заданной плоской системы сил относительно точки А, если расстояние l = 0,5 м. (Ответ 8,48)
2.2.11. К вершинам квадрата приложены шесть сил по 4Н каждая. Определить главный момент заданной плоской системы сил относительно точки B, если расстояние l = 0,4 м. (Ответ 4,99)
2.2.12. К вершинам прямоугольного треугольника приложены силы F1 = 12Н, F2 = 4Н, F3 = 2Н. Определить значение угла α в градусах, при котором главный вектор данной системы сил параллелен оси Оу. (Ответ 60,0)
2.2.13. К прямоугольнику приложены силы F1 = 4Н, F2 = 5Н, F3 = 8Н, F4 = 2Н. Определить главный момент заданной системы сил относительно точки А, если расстояние l = 1 м, угол α = 30°. (Ответ 6,89)
2.2.14. К правильному шестиугольнику приложены пять равных по модулю сил. Определить в градусах угол между главным вектором этой системы сил и осью Ох. (Ответ 180)
2.2.15. Задана плоская система сил F1 = F2 = F3 = 2H, F4 = 10Н. Определить главный момент лой системы сил относительно точки А, если радиус r = 1 м. (Ответ 11,3)
2.2.16. При каком значении угла α равнодействующая системы трех сил будет направлена вертикально, если силы F1 = 3,46Н, F2 = 2Н, F3 = 4Н? (Ответ 60,0)
2.2.17. Задана плоская система сил F1 = F2 = F3= F4 = 4Н, F5 = 5Н. Определить модуль главного вектора этой системы сил. (Ответ 5,0)
2.2.18. На каком кратчайшем расстоянии oт точки А проходит линия действия равнодействующей системы четырех сил, если F1 = F2 =F3 = F4 = 1H, расстояние l = 0,1 м? (Ответ 0.05)
2.2.19. На каком расстоянии d нужно приложить силу F = 100Н, для того чтобы линия
действия равнодействующей этой силы и распределенной нагрузки интенсивностью
qmax = 3 Н/м прошла через точку А, если расстояние l = 10м, угол α = 60°? (Ответ 4,0)
2.2.20. Какой угол в градусах с осью Ох составляет равнодействующая системы сил,
если F1 = F2 = F3 = F4? (Ответ 45,0)
2.2.21. К квадрату приложена система четырех сил, причем силы F1 = F2 = F3 = 1Н.
Определить модуль силы F4, при которой равнодействующая системы R = 2Н. (Ответ 1,0)
Видео:2.2. Главный вектор и главный момент плоской системы сил. Приведение к простейшему видуСкачать
Система сил. Главный вектор системы сил.
Системой сил = (Рис.4).называется множество сил, приложенных к точкам механической системы.
Главным вектором системы сил называется векторная сумма всех сил системы:
Найти главный вектор можно, построив в произвольном центре О векторный многоугольник, в котором начало последующей силы совпадает с концом предыдущей (рис.4). Замыкающая сторона многоугольника и есть главный вектор V системы сил.
Для пространственной системы сил построить многоугольник практически трудно. Проще найти главный вектор аналитически. Проектируя слагаемые формулу (6) на оси координат, определим проекции главного вектора, его модуль и направляющие косинусы:
Vx=Fkx; Vy=Fky; Vz=Fkz (7)
V2=Vx2+Vy2+Vz2; Cos(V,x)=Vx/V; Cos(V,y)=Vy/V; Cos(V,z)=Vz/V
Момент силы относительно точки. Теоремы о моменте
Пусть сила F приложена в точке А тела, имеющей радиус-вектор r относительно центра О.
Моментом силы F относительно центра О называется вектор
Направление векторного произведения усдовно и зависит от ориентированности пространства. Ориентированность пространства- это принятое нами правило соответствия прямой и дуговой стрелок: правого или левого винта. Вектора, направление которых зависит от оринтированности пространства, называются аксиальными. Важно, что для них (Рис.5) дуговая стрелка составляет физическую сущность (показывает направление вращения) а направление самого вектора условено.
Мы будем работать в право ориентированном пространстве и направление векторного произведения всегда будем определять пл правилу правого винта: с конца mo видно , что сила стремится повернуть тело против часовой стрелки.
Модуль момента равен произведению модуля силы на плечо h -длину перпендикуляра, опущенного из центра О на линию действия силы.
Очевидно, что момент силы тем меньше, чем меньше ее плечо, и он обращается в ноль для любого центра на линии действия силы. Вы это ощущаете, поднимая воротом ведро из колодца, и поэтому стараетесь приложить силу руки так, чтобы создать большее плечо. Из формулы для модуля момента ясно, что момент силы равен нулю только относительно точки, лежащей на линии действия силы.
Теорема 1. О зависимости момента от центра
Рис.6 а) в общем случае момент силы зависит от центра б) перенос центра параллельно линии действия силы не изменяет момента
Найдем связь между моментами силы F относительно центров А и В. Из Рис.6 ясно, что
rA= AB+rB mA(F)=rAxF=(AB+rB)xF= rBxF +ABxF
Теорема 2. О проекциях моментов.
Проектируя (10) на ось z, проходящую через А и В, находим
Таким образом приходим к лемме:
поскольку произведение АВ Х F перпендикулярно АВ и его проекция на z равна нулю. Проекции моментов силы относительно всех точек одной оси на эту ось равны между собой. Таким образом проекция моментов на ось характеризует действие силы по отношению к этой оси, поэтому называется моментом сил относительно. Матричное вычисление векторного произведения (момента). Присоединенная матрица. Известно, что векторное произведение можно представить в виде определителя матрицы
c=a x b == (aFz-zFy)i+(zFx-xFz)j+(xFy-yFx)k (12)
mo(F)=r x F== (yFz-zFy)i+(zFx-xFz)j+(xFy-yFx)k
Здесь i, j, k — орты осей x, y, z с началом в центре О, x, y, z — проекции радиуса-вектора r на эти оси.
В матричной алгебре вектору соответствует столбец его проекций на декартовы оси.
Таким образом вектор-столбец момента имеет вид
Легко убедится, что этот же результат можно получить, умножив кососимметричную матрицу, составленную из элементов столбца r
на вектор-столбец сил F (1).
Матрица R называется присоединенной матрицей вектора r
В общем случае столбец проекций векторного произведения c=a b удобно находить через присоединенную кососимметричную матрицу первого сомножителя часовой стрелки
Видео:§4.3. Главный вектор и главный момент сил инерцииСкачать
Таким образом, имеем пять независимых уравнений равновесия.
Практически для решения задач на плоскости достаточно трех уравнений равновесия. В каждом конкретном случае используются уравнения с одним неизвестным.
Для разных случаев используются три группы уравнений равновесия.
Для частного случая, если уравновешена система параллельных сил, можно составить только два уравнения равновесия:
Ось Ох системы координат параллельна линии действия сил.
Примеры решения задач
Пример 1. Найти момент присоединенной пары при переносе силы F3 в точку В (рис. 5.3).F1 = 10кН;F2 = 15кН; F3 = 18кН; а = 0,2 м.
Решение
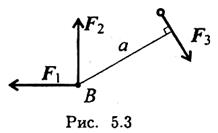
Используем теорему Пуансо.
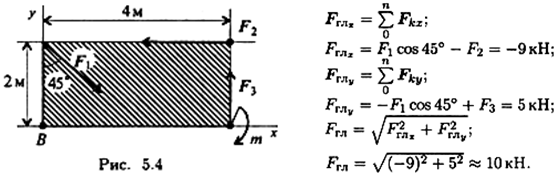
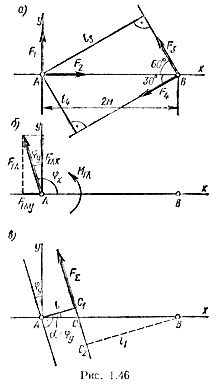
Пример 2. Найти главный вектор системы (рис. 5.4). F1 = 10кН; F2 = 16кН;F3= 12кН;т = 60кН-м.
Решение
Главный вектор равен геометрической сумме сил:
 |
Пример 3. Найти главный момент системы относительно точки В (использовать данные примера 2).
Решение
Главный момент равен алгебраической сумме моментов сил относительно точки приведения:
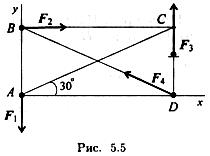
Пример 4. К телу приложена уравновешенная система сил (рис. 5.5). Две из них неизвестны. Определить неизвестные силы.
Решение
 |
Наносим оси координат и используем уравнения равновесия:
Пример 5. К двум точкам тела приложены четыре силы F1 = F2 = F3 = F4 = 5 Н, как показано на рис. 1.46, а. Привести эти силы к точке А, а затем найти их равнодействующую.
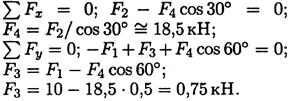Решение
1. Центр приведения (точка А) задан. Поэтому примем точку А за начало координат и проведем ось х вдоль отрезка АВ, а ось у — по линии действия силы F1 (рис. 1.46, а).
Отсюда проекция на ось х главного вектора
3.Определим проекции сил на ось у:
Отсюда проекция на ось у главного вектора
Для большей наглядности и облегчения дальнейшего решения задачи целесообразно найденные проекции Fгл х и Fгл у главного вектора отложить вдоль осей координат (рис. 1.46, б).
4. Из формулы (1,27) определим модуль главного вектора:
5. Находим угол 
По таблицам или с помощью счетной логарифмической линейки определяем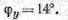 
Из рис. 1.46, б следует, что 
6. Определяем главный момент, как алгебраическую сумму моментов данных сил относительно точки А МА(F1) = 0 и МА(F2) = 0, так как линия действия сил F1 и F2 проходит через точку А (центр приведения);
Главный момент MГЛ > 0, значит он действует против хода часовой стрелки (рис. 1.46, б).
Равнодействующая FΣ = Fгл и линия ее действия, параллельная главному вектору, проходит от центра приведения А на расстоянии
Линия действия равнодействующей пересекает ось х в точке С и отсекает отрезок
Таким образом, равнодействующая заданной на рис. 1.46, а системы сил FΣ = 7,07 Н, линия ее действия образует с выбранными осями координат углы φх = 104°, φу =14° и пересекает отрезок АВ в точке С на расстоянии АС = 54 см.
Тот же результат был бы получен при выборе за центр приведения точки В, но в этом случае получилось бы ВС2 = 1,42 м и BС
146 см (рис, 1,46, б). Проверьте: так ли это.
Контрольные вопросы и задания
1. Чему равен главный вектор системы сил?
2. Чему равен главный момент системы сил при приведении ее к точке?
3. Чем отличается главный вектор от равнодействующей плоской системы произвольно расположенных сил?
Выбрать из предложенных ответов:
· величиной и направлением;
4. Тело движется равномерно и прямолинейно (равновесие). Чему равны главный вектор и главный момент системы?
5. Тело вращается вокруг неподвижной оси. Чему равны главный вектор и главный момент действующей на него системы сил?
 |
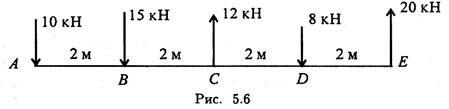6. Найдите главный вектор и главный момент системы сил, если центр приведения находится в точке А (рис. 5.6).
7. Какое еще уравнение равновесия нужно составить, чтобы убедиться в том, что система сил (рис. 5.7) находится в равновесии?
🔥 Видео
Техническая механика/ Определение равнодействующей. Плоская система сходящихся сил.Скачать
Преобразование систем сил Часть 2Скачать
5.3. Главный момент произвольной пространственной системы силСкачать
Система сходящихся силСкачать
Видеоурок 1. Определение реакций жёстких стержней.Скачать
СКД Лекция 03 ПОЛНАЯ Момент силы Теория пар силСкачать
Основная теорема статикиСкачать
Приведение системы сил к простейшему видуСкачать
Инварианты статикиСкачать
Система сходящихся сил. Решение задач по МещерскомуСкачать
2.4. Равновесие произвольной плоской системы сил (1 из 4)Скачать
Лекция 1 СТАТИКА ТВЕРДОГО ТЕЛА. Векторная алгебра сил https://stepik.org/course/71088/syllabusСкачать
Термех. Статика. Приведение пространственной системы сил к центруСкачать
Теоретическая механика. Нахождение реакций связей на при плоской системе сил. Задача 1, часть 1Скачать
#14 СТАТИКА. Равновесие тел. РЫЧАГИ. Момент силСкачать
Видеоурок 2. Определение реакций двухопорных балок.Скачать
Центральная винтовая осьСкачать
