Найти координаты вектора заданного матрицей

Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Координаты вектора в базисе

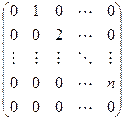
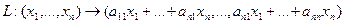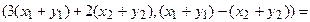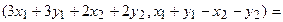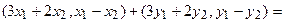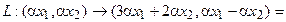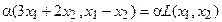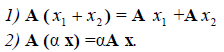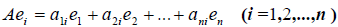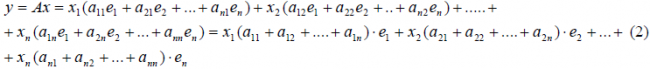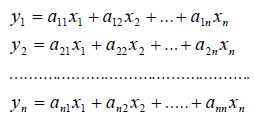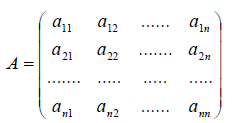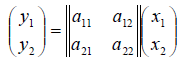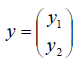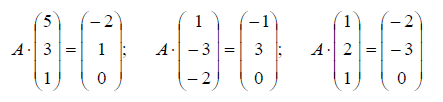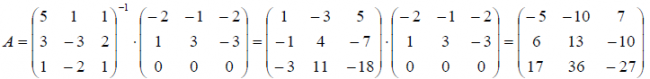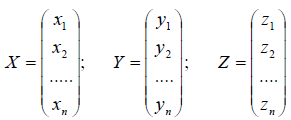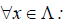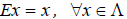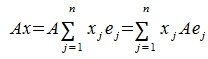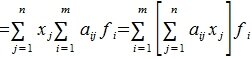Пример №1 . Даны векторы ε₁(2;1;3), ε₂(3;-2;1), ε₃(1;-3;-4), X(7;0;7). Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора X в этом базисе.
Решение. Данная задача состоит из двух частей. Сначала необходимо проверить, образуют ли векторы базис. Векторы образуют базис, если определитель, составленный из координат этих векторов, отличен от нуля, в противном случае вектора не являются базисными и вектор X нельзя разложить по данному базису.
Вычислим определитель матрицы:

∆ = 2*((-2)*(-4) — (-3)*1) — 3*(1*(-4) — (-3)*3) + 1*(1*1 — (-2)*3) = 14
Определитель матрицы равен ∆ =14
Так как определитель отличен от нуля, то векторы образуют базис, следовательно, вектор X можно разложить по данному базису. Т.е. существуют такие числа α₁α₂α₃, что имеет место равенство:
X = &#945₁ε₁ + &#945₂ε₂ + &#945₃ε₃
Запишем данное равенство в координатной форме:
(7;0;7) = α(2;1;3) + α(3;-2;1) + α(1;-3;-4)
Используя свойства векторов, получим следующее равенство:
(7;0;7) = (2α₁;1α₁;3α₁😉 + (3α₂;-2α₂;1α₂😉 + (1α₃;-3α₃;-4α₃😉
(7;0;7) = (2α₁ + 3α₂ + 1α₃;1α₁ -2α₂ -3α₃;3α₁ + 1α₂ -4α₃)
По свойству равенства векторов имеем:
2α₁ + 3α₂ + 1α₃ = 7
1α₁ -2α₂ -3α₃ = 0
3α₁ + 1α₂ -4α₃ = 7
Решаем полученную систему уравнений методом Гаусса или методом Крамера.
Ответ:

X = 2ε₁ + ε₂

В системе векторов a₁, a₂, a₃, a₄ найти любую подсистему векторов, которые образуют базис, разложить векторы по базису, перейти к другому базису, найти коэффициенты разложения векторов во втором базисе; в обоих случаях определить обратные матрицы, соответствующие векторам базиса. Правильность вычисления в каждом случае проверить с помощью умножения вектора слева на матрицу, обратную матрице вектора базиса.

Пример №2 . В системе векторов a₁, a₂, a₃, a₄ найти любую подсистему векторов, которые образуют базис, разложить векторы по базису, перейти к другому базису, найти коэффициенты разложения векторов во втором базисе; в обоих случаях определить обратные матрицы, соответствующие векторам базиса. Правильность вычисления в каждом случае проверить с помощью умножения вектора слева на матрицу, обратную матрице вектора базиса.
a₁=(1;5;3), a₂=(2;1;-1), a₃=(4;2;1), a₄=(17;13;4).

Видео:Координаты вектора. 9 класс.Скачать

Координаты и преобразования координат в линейном пространстве

Видео:Координаты в новом базисеСкачать

Координаты векторов в данном базисе линейного пространства

Пусть — базис линейного пространства . Каждый вектор можно разложить по базису (см. теорему 8.1), т.е. представить в виде , причем коэффициенты в разложении определяются однозначно. Эти коэффициенты называются координатами вектора в базисе (или относительно базиса ). Координаты вектора — это упорядоченный на бор чисел, который представляется в виде матрицы-столбца и называется координатным столбцом вектора (в данном базисе). Вектор и его координатный столбец обозначаются одной и той же буквой полужирной или светлой соответственно.

Если базис (как упорядоченный набор векторов) представить в виде символической матрицы-строки , то разложение вектора по базису можно записать следующим образом:

Здесь умножение символической матрицы-строки на числовую матрицу-столбец производится по правилам умножения матриц.

При необходимости, если речь идет о разных базисах, у координатного столбца указывается обозначение базиса, относительно которого получены координаты, например, — координатный столбец вектора в базисе .

Из теоремы 8.1 следует, что равные векторы имеют равные соответствующие координаты (в одном и том же базисе), и наоборот, если координаты векторов (в одном и том же базисе) соответственно равны, то равны и сами векторы .

Видео:Как найти координаты вектора?Скачать

Линейные операции в координатной форме

Пусть — базис линейного пространства , векторы и имеют в этом базисе координаты и соответственно, т.е.

Складывая эти равенства, получаем .

т.е. при сложении векторов их координаты складываются .

Умножая второе равенство в (8.7) на число , получаем

т.е. при умножении вектора на число все его координаты умножаются на это число .

Другими словами, сумма векторов имеет координаты , а произведение имеет координаты . Разумеется, что все координаты получены в одном базисе .

1. Нетрудно показать, что координатный столбец линейной комбинации векторов равен линейной комбинации координатных столбцов этих векторов.

2. Если система векторов линейно зависима (линейно независима), то их координатные столбцы, полученные относительно одного базиса, образуют линейно зависимую (соответственно, линейно независимую) систему. Это следует из равносильности равенств и . Например, если в этих равенствах не все коэффициенты равны нулю, т.е. система векторов и система их координатных столбцов линейно зависимы одновременно.

3. Все свойства линейной зависимости и линейной независимости векторов переносятся без изменений на их координатные столбцы, полученные в одном и том же базисе. И наоборот, свойства для матриц-столбцов, переносятся на векторы, если матрицы-столбцы считать их координатными столбцами.

4. Выбрав в n-мерном вещественном линейном пространстве некоторый базис, можно установить взаимно однозначное соответствие: каждому вектору поставить в соответствие его координатный столбец (в вы бранном базисе), и наоборот, каждому координатному столбцу поставить в соответствие вектор. Другими словами, любой фиксированный базис n-мерного вещественного линейного пространства позволяет установить взаимно однозначное соответствие между всеми векторами вещественно го пространства и всеми столбцами n-мерного арифметического пространства . Это соответствие обозначается . Для n-мерного комплексного линейного пространства аналогичное взаимно однозначное соответствие устанавливается с пространством .

Видео:Нахождение координат вектора. Практическая часть. 9 класс.Скачать

Преобразование координат вектора при замене базиса

Пусть заданы два базиса пространства и . Базис будем условно называть «старым», а базис — «новым». Пусть известны разложения каждого вектора нового базиса по старому базису:

Записывая по столбцам координаты векторов в базисе , составляем матрицу:

Квадратная матрица , составленная из координатных столбцов векторов нового базиса в старом базисе , называется матрицей перехода от старого базиса к новому. При помощи матрицы перехода (8.9) формулы (8.8) можно записать в виде:

Умножение символической матрицы-строки на матрицу перехода в (8.10) производится по правилам умножения матриц.

Пусть в базисе вектор имеет координаты , а в базисе — координаты , т.е.

Подставляя в правую часть последнего равенства выражение (8.10), получаем — два разложения вектора в одном и том же базисе . Коэффициенты этих разложений должны совпадать (по теореме 8.1), так как это координаты одного и того же вектора в одном базисе. Поэтому

Формула (8.11) устанавливает связь координат вектора в разных базисах: координатный столбец вектора в старом базисе получается в результате умножения матрицы перехода на координатный столбец вектора в новом базисе .

Пример 8.3. В пространстве многочленов степени не выше второй даны две системы многочленов:

Доказать, что каждая система является базисом пространства . Найти матрицу перехода от базиса к базису . Определить координаты квадратного трехчлена относительно базисов и .

Решение. Система многочленов является стандартным базисом пространства . Докажем, что система является базисом. По ступим следующим образом. Найдем координатные столбцы этих многочленов в стандартном базисе. Раскладывая по базису , получаем

Составим из этих столбцов матрицу . Ранг этой матрицы равен 3, так как . Следовательно, столбцы линейно независимы, тогда и многочлены линейно независимы (см. пункт 2 замечаний 8.5). Итак, многочлены являются базисом пространства , а матрица — искомая матрица перехода от базиса к базису . Осталось найти координаты многочлена в этих базисах. Раскладывая по базисам, находим

Проверим результат, вычисляя по формуле (8.11):

Видео:Собственные векторы и собственные значения матрицыСкачать

Свойства матрицы перехода от одного базиса к другому

1. Пусть имеются три базиса пространства и известны матрицы перехода: от базиса к базису ; от к ; от к . Тогда

Действительно, запишем связь (8.10) для данных базисов:

Подставляя первое выражение во второе равенство, получаем . Сравнивая с третьим равенством, приходим к (8.12).

2. Если — матрица перехода от базиса к базису , то матрица обратима и обратная матрица является матрицей перехода от базиса к базису . Координаты вектора в базисах и связаны формулами:

В самом деле, пусть — матрица перехода от базиса к базису . Учитывая, что матрица перехода от базиса к базису — единичная, применяем свойство 1 к трем базисам . Для трех базисов аналогично получаем: . Следовательно, .

3. Всякая обратимая квадратная матрица n-го порядка может служить матрицей перехода от одного базиса n-мерного линейного пространства к другому базису.

Пример 8.4. В двумерном арифметическом пространстве даны два базиса: и . Найти матрицу перехода от базиса к базису и координаты вектора в каждом из базисов.

Решение. Рассмотрим стандартный базис пространства . Находим координаты векторов в стандартном базисе. Раскладываем вектор

В стандартном базисе пространства координатный столбец совпадает с вектором . Для других векторов аналогично получаем . Из координатных столбцов составим матрицы перехода (8.9) от стандартного базиса к данным базисам и

По свойству 1 матриц перехода имеем . .По свойству 2: . Поэтому

В стандартном базисе пространства координатный столбец совпадает с вектором . Найдем координаты этого вектора в базисе (по свойству 2 матрицы перехода):

В самом деле, справедливо разложение

Найдем координаты вектора в базисе двумя способами

Полученный результат подтверждает разложение:

Видео:Найдите разложение вектора по векторам (базису)Скачать

Матрица линейного оператора примеры

Видео:9 класс, 2 урок, Координаты вектораСкачать

Построение матрицы по заданной формуле отображения.

Пусть отображение задано с помощью формулы:

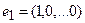
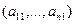
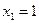
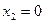
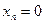
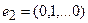
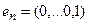
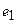
то есть для координат произвольного исходного вектора определены координаты его образа. Тогда, рассматривая вместо произвольного вектора x вектор , найдём его образ, это будет вектор . Для этого в формуле, задающей образ вектора, полагаем , ,…, . Аналогично находим образы для ,…, . Из координат образа вектора составляем 1-й столбец матрицы линейного оператора, аналогично из координат последующих векторов – остальные столбцы. Рассмотрим на примере.

Пример 1. Пусть оператор задан с помощью формулы:

.

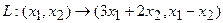
Прежде всего, докажем, что это отображение – действительно линейный оператор.

Отобразим сумму векторов:

Теперь каждую координату получившегося вектора можем преобразовать:

.

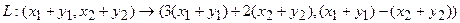
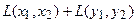
Аналогично для умножения на константу:

Для того чтобы найти матрицу этого линейного оператора, нужно, как было сказано выше, подставить значения x₁ = 1, x₂ = 0, а затем x₁ = 0, x₂ = 1. В этом примере образы базисных векторов – соответственно (3, 1) и (2, -1).

Поэтому матрица линейного оператора будет иметь вид:

.

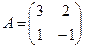
Аналогичным способом решается задача и для 3 и большего количества переменных.

Пример 2. .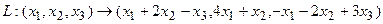

Построим матрицу оператора. Отображая вектор (1,0,0), получаем (1,4,-1), соответственно (0,1,0) переходит в (2,1,-2), а вектор (0,0,1) – в (-1,1,3).

Матрица линейного оператора:

.

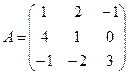
2.2. Построение матрицы оператора в случае, когда известен исходный базис и система векторов, в которую он отображается.

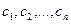
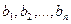
Если задана система из n векторов, образующих базис, и какая-нибудь произвольная система n векторов (возможно, линейно-зависимая), то однозначно определён линейный оператор, отображающий каждый вектор первой системы в соответствующий вектор второй системы.

Матрицу этого оператора можно найти двумя способами: с помощью обратной матрицы и с помощью системы уравнений.

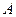
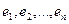
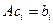
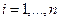
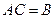
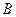
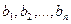
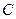
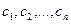
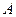
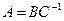
Пусть – матрица оператора в базисе . По условию, для всех индексов . Данные n равенств можно записать в виде одного матричного равенства: , при этом столбцы матрицы – это векторы , а столбцы матрицы – векторы . Тогда матрица может быть найдена в виде .

Пример. Найти матрицу линейного оператора, отображающего базис

в систему векторов .

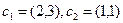
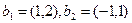
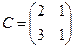
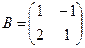
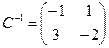
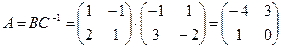
Здесь , , , и получаем:

.

Проверка осуществляется умножением получившейся матрицы на каждый вектор: .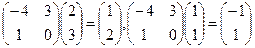

Аналогично решаются подобные задачи и для трёхмерного пространства. В приложении (§5) есть несколько вариантов таких задач.

2.3. Прочие способы нахождения матрицы оператора.

Существуют также примеры, где линейный оператор задаётся другими способами, отличными от рассмотренных в п. 2.1 и 2.2.

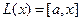
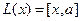
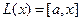
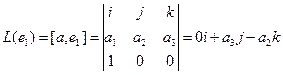
Пример. Линейными операторами являются как правое, так и левое векторное умножение на фиксированный вектор в трёхмерном пространстве, то есть отображения вида и . Построим матрицу одного из этих операторов, . Для этого найдём образы всех трёх базисных векторов линейного пространства.

.

Аналогично, ,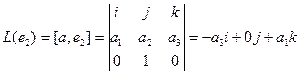

.

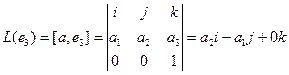
Координаты полученных векторов запишем в виде столбцов матрицы оператора.

Матрица оператора: .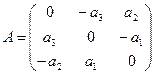

Аналогично можно построить матрицу линейного оператора :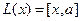

.

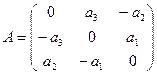
Пример. Линейный оператор дифференцирования в пространстве всех многочленов степени не более n. Это пространство размерности n + 1. Возьмём в качестве базиса элементы , , ,…, .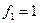

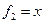
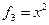
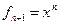
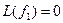
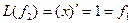
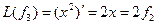
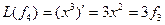
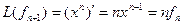
, , , аналогично получим ,…, .

Матрица этого линейного оператора:

Линейные операторы могут отображать не только пространства конечной размерности, но и бесконечномерные пространства. Так, оператор дифференцирования может рассматриваться также в пространстве всех непрерывных функций. (В этом пространстве нет конечного базиса). В этом случае, очевидно, оператор не может быть задан матрицей конечного порядка.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10219 – | 7588 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Видео:Координаты вектора.Скачать

Матрица линейного оператора

Определение 1. Если задан закон, который каждому вектору x?? ставит в соот ветствие вектор y . то говорят, что в линейном пространстве ? задан оператор A , при этом пишут:

Определение 2. Оператор A называется линейным, если для любых x 1 ?? и x 2 ?? и произвольного числа ? выполняются условия:

Рассмотрим теперь в евклидовом пространстве E n базис e 1 ,e 2 . e n и пусть в этом пространстве определён линейный оператор A : y = A x .

Разложим векторы x и y по базису e 1 ,e 2 . e n :

В силу линейности оператора A можно написать

Заметим, что каждый вектор 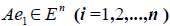, следовательно, его также можно разложить по базису e 1 ,e 2 . e n , т.е.

В силу единственности разложения по данному базису мы можем при равнять коэффициенты при базисных векторах в правых частях формул (1) и (2); тогда получим:

Получили, что линейному оператору A в данном базисе соответствует квадратная матрица

которая называется матрицей линейного оператора A , i -й столбец которой состоит из координат вектора Ae i (i = 1,2. n ) относительно данного базиса. Отметим, что матрица A оператора A зависит от выбора базиса e 1 ,e 2 . e n .

Итак, мы показали, что всякому линейному оператору A в евклидовом пространстве E n соответствует матрица A ; можно доказать и обратное утверждение: всякую квадратную матрицу A можно рассматривать как матрицу некоторого линейного оператора A в данном базисе e 1 ,e 2 . e n .

Представляют интерес невырожденные линейные операторы, т.е. такие операторы, матрицы которых имеют обратную A -1 , т.е. также являются невырожденными. В этом случае каждому вектору y (образу), определённому соотношением, отвечает единственный вектор x (прообраз) и при этом имеет место матричное равенство: X = A -1 ? Y .

Видео:Координаты точки и координаты вектора 1.Скачать

Примеры линейных операторов

1. В пространстве 2-мерных векторов линейным оператором является правило

связывающее вектор-прообраз 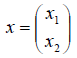с вектором-образом

2. В пространстве бесконечно дифференцируемых функций линейным оператором является операция дифференцирования, ставящая в соответствие каждому элементу этого простран ства его производную функцию.

3. В пространстве многочленов P n (t) линейным оператором является операция умножения многочлена на независимую переменную t .

Пример: Известны образы базисных векторов E 3 под действием оператора A :

Найти матрицу этого оператора в исходном базисе.

Решение: По определению y = A x, значит в матричном виде можно записать, что A = X -1 Y . Для нашего примера получаем

Видео:№934. Найдите координаты вектора АВ, зная координаты его начала и конца: а) А (2; 7), B (-2; 7);Скачать

Действия над операторами

Сложение линейных операторов. Пусть x?E n , A и B – два линейных оператора в этом пространстве.

Определение 1. Суммой линейных операторов A и B в E n называется оператор C, определяемый равенством Cx = A x + Bx , где x – любой вектор из E n .

Сумма линейных операторов является линейным оператором, причём его матрица C = A + B, где A и B – матрицы линейных операторов A и B .

Умножение линейного оператора на число. Пусть x?E n , линейный оператор A определён в E n , ? – некоторое число.

Определение 2. Произведением линейного оператора A на число ? называется оператор ?A , определяемый равенством .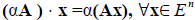

?A является линейным оператором, а матрица этого линейного оператора получается из матрицы A умножением её на число ? , т.е. она равна ? ? A.

Умножение линейных операторов. Пусть x? E n , y ? E n , z ? E n и кроме того в E n определены линейные операторы A и B таким образом, что y = Bx, z = A y .

Определение 3. Произведением A ? B линейных операторов A и B называется оператор C, определяемый соотношением Cx = A (Bx) .

Таким образом, перемножение линейных операторов состоит в последовательном их применении по отношению к вектору x .

Рассмотрим матрицы – столбцы:

и обозначим через A, B и C – соответственно матрицы линейных операторов A, B и C. Тогда Z = A ? (B ? X) = (A ? B) ? X = C ? X , таким образом, C = A ? B, т.е. матрица произведения линей ных операторов также является линейным оператором.

a) (A ? B)(x + y) = A (B(x + y)) = A (Bx + By) = A (Bx) + A (By) = = (A ? B) ? x + (A ? B) ? y

б) (A ? B)(? x) = A (B(? x)) = A (?Bx) =?A (Bx) =? (A ? B)x

Свойства умножения линейных операторов вытекают из свойств умножения матриц.

Определение 4. Линейные операторы A и В называются равными, если 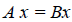. Равенство операторов обозначается как A = B .

Определение 5. Оператор E называется единичным (или тождественным) оператором, если каждому элементу x линейного пространства 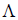он ставит в соответствие тот же самый элемент, то есть

Видео:Собственные значения и собственные векторы матрицы (4)Скачать

1. Понятие линейного оператора

Пусть R и S линейные пространства, которые имеют размерность n и m соответственно. Оператором A действующим из R в S называется отображение вида , сопоставляющее каждому элементу x пространства R некоторый элемент y пространства S. Для этого отображения будем использовать обозначение y= A(x) или y= Ax.

Определение 1. Оператор A действующий из R в S называется линейным, если для любых элементов x₁ и x₂ пространства R и любого λ из числового поля K выполняются соотношения

Если пространство S совпадает с пространством R, то линейный оператор, который действует из R в R называют линейным преобразованием пространства R.

Пусть заданы два векторных пространства n-мерный R и m-мерный S, и пусть в этих пространствах заданы базисы и соответственно. Пусть задано отображение

где A – m×n -матрица с коэффициентами из поля K. Тогда каждому элементу из R соответствует элемент y=Ax из S. Отображение (1) определяет оператор A. Покажем, что этот оператор обладает свойством линейности. Действительно, учитывая свойства умножения матриц, можно записать:

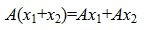,	(2)
.

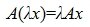Покажем теперь обратное, т.е. что для любого линейного оператора A, отображающего пространство R в S и произвольных базисов и в R и S соответственно, существует такая матрица A с элементами из численного поля K, что определяемое этой матрицей линейное отображение (1) выражает координаты отображенного вектора y через координаты исходного вектора x.

Пусть x − произвольный элемент в R. Тогда

(3)

является разложением x в по базису .

Применим оператор A к базисным векторам :

(4)

где a_ij − координаты полученного вектора в базисе .

Тогда применяя оператор A к элементу x и учитывая (3) и (4), имеем

Сделаем следующее обозначение:

(6)

Тогда равенство (5) примет следующий вид:

(7)

Из равенства (7) следует, что любой элемент из пространства R при отображении оператором A, в пространстве S и в базисе имеет координаты y_i, i=1,2. m. В свою очередь, из (6) следует, что этим координатам соответствуют линейные комбинации координатов элемента x_j, j=1,2. n с коэффициентами a_ij i=1,2. m; j=1,2. n.

Построим матрицу A с элементами a_ij:

(8)

Тогда выражение (6) можно записать в матричном виде:

Матрица A называется матрицей линейного оператора в заданных базисах и .

Видео:Как разложить вектор по базису - bezbotvyСкачать

2. Сложение линейных операторов

Пусть A и B два линейных оператора действующих из R в S и пусть A и B – mxn − матрицы соответствующие этим операторам.

Определение 2. Суммой линейных операторов A и B называется оператор C, определяемый равенством

где x∈R означает, что x принадлежит пространстве R.

Сумма линейных операторов обозначается так C=A+B. Легко убедится, что сумма линейных операторов также является линейным оператором.

Применим оператор C к базисному вектору e_j, тогда:

Следовательно оператору C отвечает матрица ,где i=1,2. m, j=1,2. n, т.е.

Видео:Векторное произведение векторов | Высшая математикаСкачать

3. Умножение линейных операторов

Пусть заданы три линейных пространства R, S и T. Пусть линейный оператор B отображает R в S, а линейный оператор A отображает S в T.

Определение 3. Произведением операторов A и B называется оператор C, для которого выполняется следующее равенство при любом x из R:

Произведение линейных операторов обозначается C=AB. Легко убедится, что произведение линейных операторов также является линейным оператором.

Таким образом оператор C отображает пространство R в T. Выберем в пространствах R, S и T базисы и обозначим через A, B и C матрицы операторов A, B и C соответствующие этим базисам. Тогда отображения линейных операторов A, B, C

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению операторов C=AB соответствует матричное произведение C=AB.

Видео:90. Координаты вектораСкачать

4. Умножение линейного оператора на число

Пусть задан линейный оператор A отображающий R в S и некоторое число λ из поля K.

Определение 4. Произведением оператора A на число λ называется оператор C, для которого выполняется следующее равенство при любом x из R:

Таким образом оператор C отображает пространство R в S. Выберем в пространствах R и S базисы и обозначим через A матрицу оператора A соответствующее этим базисам векторные равенства

можно записать в виде матричных равенств

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Учитывая произвольность х, получим

Следовательно произведению оператора C на число λ соответствует произведение матрицы A на число λ.

Видео:Базис и матрица перехода. Координаты вектора в разных базисах.Скачать

5. Нулевой оператор

Оператор, отображающий все элементы пространства R в нулевой элемент пространства S называется нулевым оператором и обозначается через O. Действие нулевого оператора можно записать так:

Видео:5 4 Координаты Преобразование координат при замене базисаСкачать

6. Противоположный оператор

Противоположным оператору A называется оператор −A удовлетворяющий равенству:

Видео:Координаты вектора в пространстве. 11 класс.Скачать

7. Ядро линейного оператора

Определение 5. Ядром линейного оператора A называется множество всех тех элементов x пространства R, для которых выполняется следующее равенство: Ax=0.

Ядро линейного оператора также называют дефектом оператора. Ядро линейного оператора обозначается символом ker A.

Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать

8. Образ линейного оператора

Определение 6. Образом линейного оператора A называется множество всех элементов y пространства R, для которых выполняется следующее равенство: y=Ax для всех x из R.

Образ линейного оператора обозначается символом im A.

Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

9. Ранг линейного оператора

Определение 7. Рангом линейного оператора A обозначаемое символом rang A называется число равное размерности образа im A оператора A, т.е.: rang A=dim(im A).