Решение:
Записываем матрицу перехода А:
и находим ее определитель
0
Видим, что ранг матрицы С равен трем. Из теоремы о базисном миноре векторы f1 , f2 , f3 линейно независимы, а поэтому могут быть приняты в качестве базиса пространства R 3 .
Находим обратную матрицу А -1 .
Транспонированная матрица:
Обратная матрица А -1
Находим координаты вектора х относительно нового базиса.
Пример №1 . Даны векторы a, b, c и d . Установить, что векторы a , b , c образуют базис, и найти координаты вектора d в этом базисе.
Решение:
Соотношение, записанное для векторов d = αa + βb + γc, справедливо для каждой из проекций:
α*1 + β*2 + γ*1 = 0
α*2 — β*2 — γ*2 = 3
α*1 + β*1 + γ0 = 1 т.е. получена алгебраическая система трёх уравнений с тремя неизвестными. Решение системы удобнее вычислять методом Крамера или методом обратной матрицы:
α = 1/2; β = 1/2; γ = -3/2
следовательно, и вектор d имеет разложение в базисе a, b, c :
d = 1/2a + 1/2b — 3/2c
Пример №2 . Даны векторы 


Пример №3 . Даны два линейных преобразования:
х’1 = a11x1 + a12x2 + a13x3, х»1 = b11x’1 + b12x’2 + b13x’3,
х’2 = a21x1 + a22x2 + a23x3, х»2 = b21x’1 + b22x’2 + b23x’3,
х’3 = a31x1 + a32x2 + a33x3, х»3 = b31x’1 + b32x’2 + b33x’3,
Средствами матричного исчисления найти преобразование, выражающее х»1, x»2, x»3 через х1, х2, х3.
х’1 = 4x1 + 3x2 + 5x3, х»1 = — x’1 + 3x’2 — 2x’3,
х’2 = 6x1 + 7x2 + x3, х»2 = — 4x’1 + x’2 + 2x’3,
х’3 = 9x1 + x2 + 8x3, х»3 = 3x’1 — 4x’2 + 5x’3,
Решение. Используя калькулятор, получаем:
Обозначим:
| A = |
|
| B = |
|
Тогда матричное уравнение запишется в виде: A·X = B.
Вычислим определитель матрицы А:
∆ = 4*(7*8 — 1*1) — 6*(3*8 — 1*5) + 9*(3*1 — 7*5) = -182
Определитель матрицы А равен detA=-182
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим слева обе части уравнения на A -1 : A -1 ·A·X = A -1 ·B, тогда получим E·X = A -1 ·B, или X = A -1 ·B.
Найдем обратную матрицу A -1 .
| A -1 = -1/182 |
|
Матрицу Х ищем по формуле:
| X = A -1 ·B = -1/182 |
| * |
| = |
|
Пример №4 . В декартовой прямой системе координат даны вершины пирамиды A(3,0,-1), B(-1,-2,-4), C(-1,2,4), D(7,-3,1). Найдите:
а) длину ребра AB;
б) косинус угла между векторами AB и AC ;
в) уравнение ребра AB;
г) уравнение грани ABC;
д) уравнение высоты, опущенной из вершины D на грань ABC;
е) координаты векторов e 1= AB , e 2= AC , e 3= AD и докажите, что они образуют линейную независимую систему;
ж) координаты вектора MN , где M и N – середины ребер AD и DC соответственно;
з) разложение вектора MN по базису ( e 1, e 2, e 3)
Решение. Пункты (а-д) решаются через онлайн калькулятор.
Задание 1 . Разложить вектор d =(8;-5) по векторам a =(1;-2) и b =(2;3).
Решение. Векторы a и b образуют базис на плоскости, так как они не коллинеарны (
Следовательно, вектор d = α a +β b , где α и β – коэффициенты, которые надо найти.
Таким образом, имеем равенство
8i-5j=α(i-2j)+β(2i+3j)=(α+2β)i+ (-2α+3β)j.
В координатной форме это равенство примет вид 
Решим полученную систему уравнений.
- Координаты и преобразования координат в линейном пространстве
- Координаты векторов в данном базисе линейного пространства
- Линейные операции в координатной форме
- Преобразование координат вектора при замене базиса
- Свойства матрицы перехода от одного базиса к другому
- Замена базиса и системы координат
- Изменение базиса.
- Изменение системы координат.
- Замена декартовой прямоугольной системы координат на плоскости.
- 🎬 Видео
Видео:Координаты в новом базисеСкачать

Координаты и преобразования координат в линейном пространстве
Видео:Базис и матрица перехода. Координаты вектора в разных базисах.Скачать

Координаты векторов в данном базисе линейного пространства
Пусть — базис линейного пространства . Каждый вектор можно разложить по базису (см. теорему 8.1), т.е. представить в виде , причем коэффициенты в разложении определяются однозначно. Эти коэффициенты называются координатами вектора в базисе (или относительно базиса ). Координаты вектора — это упорядоченный на бор чисел, который представляется в виде матрицы-столбца и называется координатным столбцом вектора (в данном базисе). Вектор и его координатный столбец обозначаются одной и той же буквой полужирной или светлой соответственно.
Если базис (как упорядоченный набор векторов) представить в виде символической матрицы-строки , то разложение вектора по базису можно записать следующим образом:
Здесь умножение символической матрицы-строки на числовую матрицу-столбец производится по правилам умножения матриц.
При необходимости, если речь идет о разных базисах, у координатного столбца указывается обозначение базиса, относительно которого получены координаты, например, — координатный столбец вектора в базисе .
Из теоремы 8.1 следует, что равные векторы имеют равные соответствующие координаты (в одном и том же базисе), и наоборот, если координаты векторов (в одном и том же базисе) соответственно равны, то равны и сами векторы .
Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Линейные операции в координатной форме
Пусть — базис линейного пространства , векторы и имеют в этом базисе координаты и соответственно, т.е.
Складывая эти равенства, получаем .
т.е. при сложении векторов их координаты складываются .
Умножая второе равенство в (8.7) на число , получаем
т.е. при умножении вектора на число все его координаты умножаются на это число .
Другими словами, сумма векторов имеет координаты , а произведение имеет координаты . Разумеется, что все координаты получены в одном базисе .
1. Нетрудно показать, что координатный столбец линейной комбинации векторов равен линейной комбинации координатных столбцов этих векторов.
2. Если система векторов линейно зависима (линейно независима), то их координатные столбцы, полученные относительно одного базиса, образуют линейно зависимую (соответственно, линейно независимую) систему. Это следует из равносильности равенств и . Например, если в этих равенствах не все коэффициенты равны нулю, т.е. система векторов и система их координатных столбцов линейно зависимы одновременно.
3. Все свойства линейной зависимости и линейной независимости векторов переносятся без изменений на их координатные столбцы, полученные в одном и том же базисе. И наоборот, свойства для матриц-столбцов, переносятся на векторы, если матрицы-столбцы считать их координатными столбцами.
4. Выбрав в n-мерном вещественном линейном пространстве некоторый базис, можно установить взаимно однозначное соответствие: каждому вектору поставить в соответствие его координатный столбец (в вы бранном базисе), и наоборот, каждому координатному столбцу поставить в соответствие вектор. Другими словами, любой фиксированный базис n-мерного вещественного линейного пространства позволяет установить взаимно однозначное соответствие между всеми векторами вещественно го пространства и всеми столбцами n-мерного арифметического пространства . Это соответствие обозначается . Для n-мерного комплексного линейного пространства аналогичное взаимно однозначное соответствие устанавливается с пространством .
Видео:Разложение вектора по базису. 9 класс.Скачать

Преобразование координат вектора при замене базиса
Пусть заданы два базиса пространства и . Базис будем условно называть «старым», а базис — «новым». Пусть известны разложения каждого вектора нового базиса по старому базису:
Записывая по столбцам координаты векторов в базисе , составляем матрицу:
Квадратная матрица , составленная из координатных столбцов векторов нового базиса в старом базисе , называется матрицей перехода от старого базиса к новому. При помощи матрицы перехода (8.9) формулы (8.8) можно записать в виде:
Умножение символической матрицы-строки на матрицу перехода в (8.10) производится по правилам умножения матриц.
Пусть в базисе вектор имеет координаты , а в базисе — координаты , т.е.
Подставляя в правую часть последнего равенства выражение (8.10), получаем — два разложения вектора в одном и том же базисе . Коэффициенты этих разложений должны совпадать (по теореме 8.1), так как это координаты одного и того же вектора в одном базисе. Поэтому
Формула (8.11) устанавливает связь координат вектора в разных базисах: координатный столбец вектора в старом базисе получается в результате умножения матрицы перехода на координатный столбец вектора в новом базисе .
Пример 8.3. В пространстве многочленов степени не выше второй даны две системы многочленов:
Доказать, что каждая система является базисом пространства . Найти матрицу перехода от базиса к базису . Определить координаты квадратного трехчлена относительно базисов и .
Решение. Система многочленов является стандартным базисом пространства . Докажем, что система является базисом. По ступим следующим образом. Найдем координатные столбцы этих многочленов в стандартном базисе. Раскладывая по базису , получаем
Составим из этих столбцов матрицу . Ранг этой матрицы равен 3, так как . Следовательно, столбцы линейно независимы, тогда и многочлены линейно независимы (см. пункт 2 замечаний 8.5). Итак, многочлены являются базисом пространства , а матрица — искомая матрица перехода от базиса к базису . Осталось найти координаты многочлена в этих базисах. Раскладывая по базисам, находим
Проверим результат, вычисляя по формуле (8.11):
Видео:Замена базиса. ТемаСкачать

Свойства матрицы перехода от одного базиса к другому
1. Пусть имеются три базиса пространства и известны матрицы перехода: от базиса к базису ; от к ; от к . Тогда
Действительно, запишем связь (8.10) для данных базисов:
Подставляя первое выражение во второе равенство, получаем . Сравнивая с третьим равенством, приходим к (8.12).
2. Если — матрица перехода от базиса к базису , то матрица обратима и обратная матрица является матрицей перехода от базиса к базису . Координаты вектора в базисах и связаны формулами:
В самом деле, пусть — матрица перехода от базиса к базису . Учитывая, что матрица перехода от базиса к базису — единичная, применяем свойство 1 к трем базисам . Для трех базисов аналогично получаем: . Следовательно, .
3. Всякая обратимая квадратная матрица n-го порядка может служить матрицей перехода от одного базиса n-мерного линейного пространства к другому базису.
Пример 8.4. В двумерном арифметическом пространстве даны два базиса: и . Найти матрицу перехода от базиса к базису и координаты вектора в каждом из базисов.
Решение. Рассмотрим стандартный базис пространства . Находим координаты векторов в стандартном базисе. Раскладываем вектор
В стандартном базисе пространства координатный столбец совпадает с вектором . Для других векторов аналогично получаем . Из координатных столбцов составим матрицы перехода (8.9) от стандартного базиса к данным базисам и
По свойству 1 матриц перехода имеем . .По свойству 2: . Поэтому
В стандартном базисе пространства координатный столбец совпадает с вектором . Найдем координаты этого вектора в базисе (по свойству 2 матрицы перехода):
В самом деле, справедливо разложение
Найдем координаты вектора в базисе двумя способами
Полученный результат подтверждает разложение:
Видео:Как разложить вектор по базису - bezbotvyСкачать

Замена базиса и системы координат
Видео:Матрица переходаСкачать
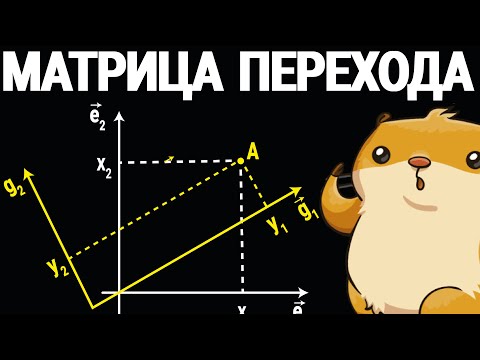
Изменение базиса.
До сих пор мы предполагали, что рассматривается один базис. Однако выбор базиса ничем не ограничен, и принципиальное значение имеет задача о нахождении компонент вектора в одном базисе по его компонентам в другом базисе. При этом положение нового базиса относительно старого должно быть задано, а именно должны быть известны компоненты новых базисных векторов (boldsymbol<e’_>), (boldsymbol<e’_>) и (boldsymbol<e’_>) в старом базисе (boldsymbol<e_>), (boldsymbol<e_>), (boldsymbol<e_>). Пусть:
$$
begin
boldsymbol<e’_> = a_^boldsymbol<e’_> + a_^boldsymbol<e’_> + a_^boldsymbol<e’_>,\
boldsymbol<e’_> = a_^boldsymbol<e’_> + a_^boldsymbol<e’_> + a_^boldsymbol<e’_>,\
boldsymbol<e’_> = a_^boldsymbol<e’_> + a_^boldsymbol<e’_> + a_^boldsymbol<e’_>,
endlabel
$$
Соотношения eqref и являются решением нашей задачи. Если нас заинтересует выражение новых компонент через старые, то надо будет решить систему уравнений eqref относительно неизвестных (alpha’_), (alpha’_), (alpha’_). Результат будет иметь такой же вид, как eqref, только коэффициентами будут компоненты старых базисных векторов в новом базисе.
Точно тем же способом получаются формулы, связывающие компоненты вектора в разных базисах на плоскости. Вот они:
$$
begin
& alpha_ = a_^alpha’_ + a_^alpha’_,\
& alpha_ = a_^alpha’_ + a_^alpha’_.
endlabel
$$
Коэффициенты в формулах eqref можно записать в таблицу:
$$
begin
a_^& a_^& a_^\
a_^& a_^& a_^\
a_^& a_^& a_^
endlabel
$$
Она называется матрицей перехода от базиса (boldsymbol<e’_>), (boldsymbol<e’_>), (boldsymbol<e’_>) к базису (boldsymbol<e_>), (boldsymbol<e_>), (boldsymbol<e_>). В ее столбцах стоят компоненты векторов (boldsymbol<e’_>), (boldsymbol<e’_>), (boldsymbol<e’_>) в старом базисе.
Видео:Найдите разложение вектора по векторам (базису)Скачать

Изменение системы координат.
Рассмотрим теперь две декартовы системы координат: старую (O), (boldsymbol<e_>), (boldsymbol<e_>), (boldsymbol<e_>) и новую (O’), (boldsymbol<e’_>), (boldsymbol<e’_>), (boldsymbol<e’_>). Пусть (M) — произвольная точка, и координаты ее в этих системах обозначены ((x), (y), (z)) и ((x’), (y’), (z’)). Поставим себе задачу выразить (x), (y) и (z) через (x’), (y’) и (z’), считая известным положение новой системы относительно старой. Оно определяется координатами ((a_^, a_^, a_^)) точки (O’) в системе координат (O), (boldsymbol<e_>), (boldsymbol<e_>), (boldsymbol<e_>) и компонентами векторов (boldsymbol<e’_>), (boldsymbol<e’_>), (boldsymbol<e’_>), составляющими матрицу перехода eqref.
Радиус-векторы точки (M) относительно точек (O) и (O’) связаны равенством (overrightarrow = overrightarrow + overrightarrow), которое мы можем записать в виде
$$
overrightarrow = overrightarrow + x’boldsymbol<e’_> + y’boldsymbol<e’_> + z’boldsymbol<e’_>,label
$$
так как (x’), (y’) и (z’) — компоненты (overrightarrow) в базисе (boldsymbol<e’_>), (boldsymbol<e’_>), (boldsymbol<e’_>). Разложим каждый член равенства eqref по базису (boldsymbol<e_>), (boldsymbol<e_>), (boldsymbol<e_>), имея в виду, что компоненты векторов (overrightarrow) и (overrightarrow) равны координатам точек (M) и (O’), которые мы обозначили ((x), (y), (z)) и ((a_^, a_^, a_^)), Мы получим
$$
begin
& x = a_^ + a_^x’ + a_^y’ + a_^z’,\
& y = a_^ + a_^x’ + a_^y’ + a_^z’,\
& z = a_^ + a_^x’ + a_^y’ + a_^z’.
endlabel
$$
Равенства eqref представляют собой закон преобразования координат точки при переходе от одной декартовой системы координат в пространстве к другой такой же системе.
Видео:Семинар №4 "Замена базиса и системы координат"Скачать

Замена декартовой прямоугольной системы координат на плоскости.
Формулы перехода от одной декартовой системы координат на плоскости к другой получаются из eqref, если там оставить только первые два равенства и в них вычеркнуть члены с (z’):
$$
begin
& x = a_^x’ + a_^y’ + a_^,\
& y = a_^x’ + a_^y’ + a_^.
endlabel
$$
Рассмотрим частный случай, когда обе системы координат декартовы прямоугольные. Через (varphi) обозначим угол между векторами (boldsymbol<e_>) и (boldsymbol<e’_>) отсчитываемый в направлении кратчайшего поворота от (boldsymbol<e_>) к (boldsymbol<e_>). Тогда (рис. 3.1)
$$
begin
& boldsymbol<e’_> = cos varphi boldsymbol<e_> + sin varphi boldsymbol<e_>,\
& boldsymbol<e’_> = cos left(varphi pm fracright) boldsymbol<e_> + sin left(varphi pm fracright) boldsymbol<e_>.
endnonumber
$$
Рис. 3.1
В разложении (boldsymbol<e’_>) ставится знак плюс, если кратчайший поворот от (boldsymbol<e’_>) к (boldsymbol<e’_>) направлен так же, как кратчайший поворот от (boldsymbol<e’_>) к (boldsymbol<e’_>), то есть если новый базис повернут относительно старого на угол (varphi). Знак минус в разложении (boldsymbol<e’_>) ставится в противоположном случае, когда новый базис не может быть получен поворотом старого.
Поскольку (displaystyle cos left(varphi pm fracright) = mp sin varphi), (displaystyle sin left(varphi pm fracright) = pm cos varphi), получаем
$$
begin
& x = x’ cos varphi mp y’ sin varphi + a_^,\
& y = x’ sin varphi pm y’ cos varphi + a_^.
endlabel
$$
причем при повороте системы координат берутся верхние знаки.
🎬 Видео
Координаты вектора. 9 класс.Скачать

Умножение вектора на число. 9 класс.Скачать

Скалярное произведение векторовСкачать

5 4 Координаты Преобразование координат при замене базисаСкачать

Векторы. Метод координат. Вебинар | МатематикаСкачать

Координаты вектора в пространстве. 11 класс.Скачать

Изменение базиса | Сущность Линейной Алгебры, глава 9Скачать

Координаты точки и координаты вектора 1.Скачать

10 класс, 38 урок, Понятие вектораСкачать

9 класс, 2 урок, Координаты вектораСкачать

Базис. Разложение вектора по базису.Скачать
