О чем эта статья:
10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Определение параллельности прямых
Начнем с главного — определимся, какие прямые параллельны согласно евклидовой геометрии. Мы недаром упомянули Евклида, ведь именно в его трудах, написанных за 300 лет до н. э., до нас дошли первые упоминания о параллельности.
Параллельными называются прямые в одной плоскости, не имеющие точек пересечения, даже если их продолжать бесконечно долго. Обозначаются они следующим образом: a II b.
Казалось бы, здесь все просто, но со времен Евклида над определением параллельных прямых и признаками параллельности прямых бились лучшие умы. Особый интерес вызывал 5-й постулат древнегреческого математика: через точку, которая не относится к прямой, в той же плоскости можно провести только одну прямую, параллельную первой. В XIX веке российский математик Н. Лобачевский смог опровергнуть постулат и указать на условия, при которых возможно провести как минимум 2 параллельные прямые через одну точку.
Впрочем, поскольку школьная программа ограничена евклидовой геометрией, вышеуказанное утверждение мы принимаем как аксиому.
На плоскости через любую точку, не принадлежащую некой прямой, можно провести единственную прямую, которая была бы ей параллельна.
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Свойства и признаки параллельных прямых
Есть ряд признаков, по которым можно определить, что одна прямая параллельна другой. К счастью, свойства и признаки параллельности прямых тесно связаны, поэтому не придется запоминать много информации.
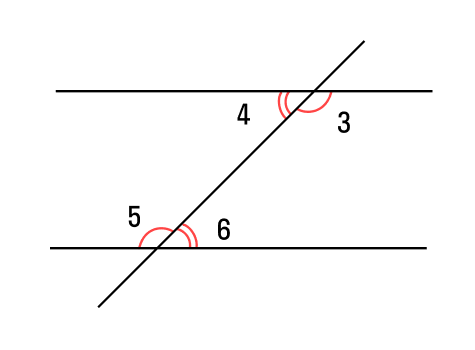
Начнем со свойств. Для этого проведем третью прямую, пересекающую параллельные прямые — она будет называться секущей. В результате у нас образуется 8 углов.
Если секущая проходит через две параллельные прямые, то:
- два внутренних односторонних угла образуют в сумме 180°:
∠4 + ∠6 = 180°; ∠3 + ∠5 = 180°.
два внутренних накрест лежащих угла равны между собой:
два соответственных угла равны между собой:
∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.
Вышеуказанные свойства являются одновременно признаками, по которым мы можем сделать вывод о параллельности прямых. Причем достаточно установить и доказать лишь один признак — остальные будут к нему прилагаться.
А сейчас посмотрим, как все это помогает решать задачи и практиковаться в определении параллельности двух прямых.
Задача 1
Прямые MN и KP пересекают две другие прямые, образуя несколько углов. Известно, что ∠1 = 73°; ∠3 = 92°; ∠2 = 73°. Требуется найти величину ∠4.
Решение
Поскольку ∠1 и ∠2 являются соответственными, их равенство говорит о том, что MN II KP. Следовательно, ∠3 = ∠MPK = 92°.
Согласно другому свойству параллельных прямых ∠4 + ∠MPK = 180°.
Задача 2
Две параллельные прямые а и b удалены друг от друга на расстояние 27 см. Секущая к этим прямым образует с одной из них угол в 150°. Требуется найти величину отрезка секущей, расположенного между а и b.
Решение
Поскольку а II b, значит ∠MKD + ∠KDN = 180°.
Соответственно, ∠MKD = 180° — ∠KDN = 180° — 150° = 30°.
Теперь рассмотрим треугольник KDM. Мы знаем, что отрезок DM представляет собой расстояние между прямыми а и b, а значит, DM ┴ b и наш треугольник является прямоугольным.
Поскольку катет, противолежащий углу в 30°, равен ½ гипотенузы, DM = 1/2DK.
Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Параллельные прямые. Признаки параллельности прямых
Как мы знаем, прямые либо пересекаются (т.е. имеют одну общую точку), либо не пересекаются (т.е. не имеют ни одной общей точки).
Определение 1. Две прямые на плоскости называются параллельными , если они не пересекаются.
Если прямые a и b параллельны, то это обозначают так:
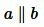 . . |
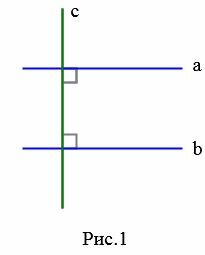
На рисунке Рис.1 изображены прямые a и b, которые перпендикулярны к прямой c. В этом случае эти прямые не пересекаются (см. статью Перперндикулярные прямые), т.е. они параллельны (Определение 1).
 |
Понятие параллельности можно распространять и на отрезки.
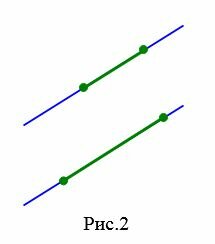
Определение 2. Два отрезка называются параллельными , если они лежат на параллельных прямых (Рис.2).
 |
Аналогично определяется параллельность отрезка и прямой, отрезка и луча, двух лучей, луча и прямой.
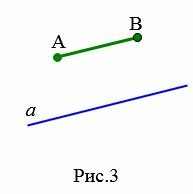 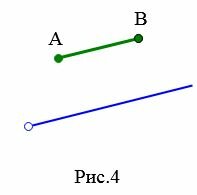 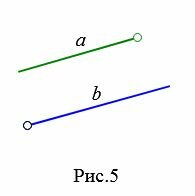 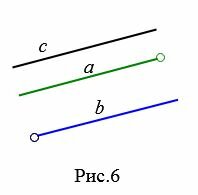 |
На Рис.3 отрезок AB пераллелен к прямой a поскольку прямая, проходящай через отроезок AB параллельна прямой a. На рисунке Рис.4 отрезок AB пераллелен к лучу a так как прямые, проходящие через отрезок AB и луч a параллельны. Для Рис.5 и Рис.6 можно сделать аналогичные рассуждения.
Видео:7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

Признаки параллельности прямых
Определение 3. Прямая c называется секущей по отношению к прямым a и b, если она пересекает их в двух точках.
При пересечении прямой c с a и b образуются восемь углов, некоторые пары из которых имеют специальные названия (Рис.7):
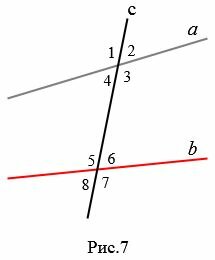 |
- накрест лежащие углы: 3 и 5, 4 и 6;
- односторонние углы: 4 и 5, 3 и 6;
- соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7.
Определим признаки параллельности двух прямых, связанные с этими парамы углов.
Теорема 1. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Доказательство. Предположим, что при пересечении прямых a и b секущей AB накрест лежащие углы равны: 
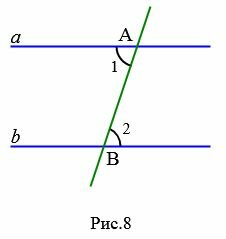 |
Докажем, что 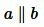
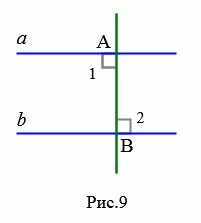
Если углы 1 и 2 прямые (Рис.9), то получается, что прямые a и b перпендикулярны прямой AB и, следовательно, они параллельны (теорема 1 статьи Перперндикулярные прямые и определение 1 настоящей статьи).
 |
Предположим, что углы 1 и 2 не прямые (Рис.10).
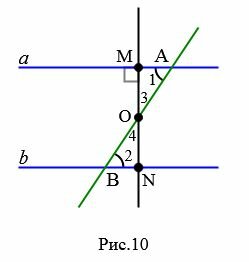 |
Найдем середину отрезка AB и обозначим через O. Из точки O проведем перпендикуляр OM к прямой a. На прямой b отложим отрезок BN равной отрезку MA. Треугольники OAM и OBN равны по двум сторонам и углу между ними, так как OA=OB, MA=NB, 
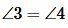
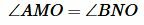
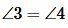
Теорема 2. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Доказательство. Пусть при пересечении прямых a и b секущей с соответственные углы равны, например 
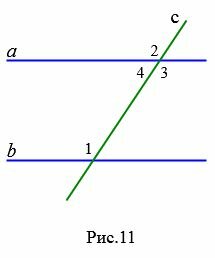 |
Так как углы 2 и 3 вертикальные, то 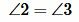

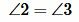
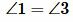
Теорема 3. Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.
Доказательство. Пусть при пересечении прямых a и b секущей с сумма односторонних углов равна 180°, например 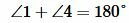
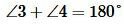
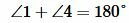
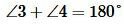
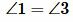
Видео:ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. СУММА УГЛОВ ТРЕУГОЛЬНИКА. Контрольная № 3. 7 классСкачать

Геометрия (7-9). Параллельные прямые. Свойства и признаки параллельных прямых
Главная > Документ
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
Свойства и признаки параллельных прямых.
1. Аксиома параллельных прямых. Через данную точку можно провести не более одной прямой, параллельной данной.
2.Если две прямые параллельны одной и той же прямой, то они параллельны между собой.
3.Две прямые, перпендикулярные одной и той же прямой, параллельны.
4.Если две прямые пересечь третьей, то образованные при этом внутренние накрест лежащие углы равны; соответственные углы равны; внутренние односторонние углы в сумме составляют 180 градусов.
5.Если при пересечении двух прямых третьей образуются равные внутренние накрест лежащие углы, то прямые параллельны.
6.Если при пересечении двух прямых третьей образуются равные соответственные углы, то прямые параллельны.
7.Если при пересечении двух прямых третьей сумма внутренних односторонних углов равна 180 градусов, то прямые параллельны.
Если на одной стороне угла отложить равные отрезки и через их концы провести параллельные прямые, пересекающие вторую сторону угла, то на второй стороне угла отложатся также равные отрезки.
Теорема о пропорциональных отрезках.
Параллельные прямые, пересекающие стороны угла, высекают на них пропорциональные отрезки.
Признаки равенства треугольников.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
Признаки равенства прямоугольных треугольников.
По двум катетам.
По катету и гипотенузе.
По гипотенузе и острому углу.
По катету и острому углу.
Теорема о сумме углов треугольника и следствия из неё.
Сумма внутренних углов треугольника равна 180 градусов.
Внешний угол треугольника равен сумме двух внутренних не смежных с ним углов.
Сумма внутренних углов выпуклого n- угольника равна 180(n-2).
Сумма внешних углов n- угольника равна 360 градусов.
Углы со взаимно перпендикулярными сторонами равны, если они оба острые или оба тупые.
Угол между биссектрисами смежных углов равен 90 градусов.
Биссектрисы внутренних односторонних углов при параллельных прямых и секущей перпендикулярны.
Основные свойства и признаки равнобедренного треугольника.
Углы при основании равнобедренного треугольника равны.
Если два угла треугольника равны, то он равнобедренный.
В равнобедренном треугольнике медиана, биссектриса и высота, проведённые к основанию, совпадают.
Если в треугольнике совпадает любая пара отрезков из троек медиана, биссектриса, высота, то он является равнобедренным.
Неравенство треугольника и следствия из него.
Сумма двух сторон треугольника больше его третьей стороны.
Сумма звеньев ломаной больше отрезка, соединяющего начало первого звена с концом последнего.
Против большего угла треугольника лежит большая сторона.
Против большей стороны треугольника лежит больший угол.
Гипотенуза прямоугольного треугольника больше катета.
Если из одной точки проведены к прямой перпендикуляр и наклонные, то
перпендикуляр короче наклонных;
большей наклонной соответствует большая проекция и наоборот.
Средняя линия треугольника. Отрезок, соединяющий середины сторон треугольника, называется средней линией треугольника.
Теорема о средней линии треугольника. Средняя линия треугольника параллельна стороне треугольника и равна её половине.
Теоремы о медианах треугольника.
Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины.
Если медиана треугольника равна половине стороны, к которой она проведена, то треугольник прямоугольный.
Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы.
Свойство серединных перпендикуляров к сторонам треугольника. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, которая является центром окружности, описанной около треугольника.
Теорема о высотах треугольника. Прямые, содержащие высоты треугольника, пересекаются в одной точке.
Теорема о биссектрисах треугольника . Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в треугольник.
Свойство биссектрисы треугольника. Биссектриса треугольника делит его сторону на отрезки, пропорциональные двум другим сторонам.
Признаки подобия треугольников.
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то треугольники подобны.
если две стороны одного треугольника соответственно пропорциональны двум сторонам другого, а углы, заключённые между этими сторонами, равны, то треугольники подобны.
Если три стороны одного треугольника соответственно пропорциональны трём сторонам другого, то треугольники подобны.
Площади подобных треугольников.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Если два треугольника имеют равные углы, то их площади относятся как произведения сторон, заключающих эти углы.
В прямоугольном треугольнике
Катет прямоугольного треугольника равен произведению гипотенузы на синус противолежащего или косинус прилежащего к этому катету острого угла.
Катет прямоугольного треугольника равен другому катету, умноженному на тангенс противолежащего или на котангенс прилежащего к этому катету острого угла.
Катет прямоугольного треугольника, лежащий в против угла в 30 градусов, равен половине гипотенузы.
Если катет прямоугольного треугольника равен половине гипотенузы, то угол, противолежащий этому катету, равен 30 градусов.

Теорема Пифагора и теорема, обратная теореме Пифагора.
Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.
Если квадрат стороны треугольника равен сумме квадратов двух других его сторон, то треугольник – прямоугольный.
Средние пропорциональные в прямоугольном треугольнике.
Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное проекций катетов на гипотенузу, а каждый катет есть среднее пропорциональное гипотенузы и своей проекции на гипотенузу.
Метрические соотношения в треугольнике.
Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
Следствие из теоремы косинусов.
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех этих сторон.
Формула для медианы треугольника.
Если m- медиана треугольника, проведённая к стороне с, то m=

Стороны треугольника пропорциональны синусам противолежащих углов.

Обобщённая теорема синусов.
Отношение стороны треугольника к синусу противолежащего угла равно диаметру окружности, описанной около треугольника.
Формулы площади треугольника.
Площадь треугольника равна половине произведения основания на высоту.
a-основание, h- высота треугольника.
2. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними. S=
3. Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности. S=pr.
4. Площадь треугольника равна произведению трёх его сторон, делённому на учетверённый радиус описанной окружности. S=
5. Формула Герона: S=
Элементы равностороннего треугольника.
Пусть h, S, r, R – высота, площадь, радиусы вписанной и описанной окружностей равностороннего треугольника со стороной a. Тогда
h= 


Параллелограммом называется четырёхугольник, противоположные стороны которого попарно параллельны.
Свойства и признаки параллелограмма.
Диагональ разбивает параллелограмм на два равных треугольника.
Противоположные стороны параллелограмма попарно равны.
Противоположные углы параллелограмма попарно равны.
Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам.
Если противоположные стороны четырёхугольника попарно равны, то этот четырёхугольник- параллелограмм.
Если две противоположные стороны четырёхугольника равны и параллельны, то четырёхугольник- параллелограмм.
Если диагонали четырёхугольника делятся точкой пересечения пополам, то этот четырёхугольник- параллелограмм.
Свойство середин сторон четырёхугольника.
Середины сторон любого четырёхугольника являются вершинами параллелограмма, площадь которого равна половине площади четырёхугольника.
Прямоугольником называется параллелограмм с прямым углом.
Свойства и признаки прямоугольника.
Диагонали прямоугольника равны.
Если диагонали параллелограмма равны, то этот параллелограмм – прямоугольник.
Квадратом называется прямоугольник, все стороны которого равны.
Ромбом называется четырёхугольник, все стороны которого равны.
Свойства и признаки ромба.
Диагонали ромба перпендикулярны.
Диагонали ромба делят его углы пополам.
Если диагонали параллелограмма перпендикулярны, то этот параллелограмм- ромб.
Трапецией называется четырёхугольник, у которого только две противоположные стороны (основания) параллельны. Средней линией трапеции называется отрезок, соединяющий середины непараллельных сторон (боковых сторон).
Теорема о средней линии трапеции. Средняя линия трапеции параллельна основаниям и равна их полусумме.
Отрезок, соединяющий середины диагоналей трапеции, равен полуразности
Замечательное свойство трапеции. Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой.
Равнобедренная трапеция. Трапеция называется равнобедренной, если её боковые стороны равны.
Свойства и признаки равнобедренной трапеции.
Углы при основании равнобедренной трапеции равны.
Диагонали равнобедренной трапеции равны.
Если углы при основании трапеции равны, то она равнобедренная.
Если диагонали трапеции равны, то она равнобедренная.
Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали- полусумме оснований.
Формулы площади четырёхугольника.
Площадь параллелограмма равна произведению основания на высоту.
Площадь параллелограмма равна произведению его соседних сторон на синус угла между ними.
Площадь прямоугольника равна произведению двух его соседних сторон. S=ab.
Площадь ромба равна половине произведения его диагоналей. 
Площадь трапеции равна произведению полусуммы оснований на высоту. 
Площадь четырёхугольника равна половине произведения его диагоналей на синус угла между ними. 
Формула Герона для четырёхугольника, около которого можно описать окружность: S= 
Отношение соответствующих линейных элементов подобных фигур равно коэффициенту подобия.
Отношение площадей подобных фигур равно квадрату коэффициента подобия.
Теорема. В любой правильный многоугольник можно вписать окружность, и притом только одну.
Окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах.
Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник.
Пусть 





Окружностью называется геометрическое место точек плоскости, удалённых от данной точки, называемой центром окружности, на одно и то же положительное расстояние.
Основные свойства окружности.
Диаметр, перпендикулярный хорде, делит хорду и стягиваемые ею дуги пополам.
Диаметр, проходящий через середину хорды, не являющейся диаметром, перпендикулярен этой хорде.
Серединный перпендикуляр к хорде проходит через центр окружности.
Равные хорды удалены от центра окружности на равные расстояния.
Хорды окружности, удалённые от центра на равные расстояния, равны.
Окружность симметрична относительно любого своего диаметра.
Дуги окружности, заключённые между параллельными хордами, равны.
Из двух хорд больше та, которая менее удалена от центра.
Диаметр есть наибольшая хорда окружности.
Замечательные свойства окружности.
Геометрическое место точек М, из которых отрезок АВ виден под прямым углом ( 
Геометрическое место точек, из которых данный отрезок виден под данным углом, есть две дуги равных окружностей (без концов этих дуг).
Касательная к окружности.
Прямая, имеющая с окружностью единственную общую точку, называется касательной к окружности.
Касательная перпендикулярна радиусу, проведённому в точку касания.
Если прямая a, проходящая через точку на окружности, перпендикулярна радиусу, проведённому в эту точку, то прямая a- касательная к окружности.
Если прямые, проходящие через точку М, касаются окружности в точках А и В, то МА=МВ и Касающиеся окружности.
Говорят, что две окружности касаются, если они имеют единственную общую точку (точку касания).
Точка касания двух окружностей лежит на их линии центров
Окружности радиусов r и R с центрами 


Окружности радиусов r и R (r Углы, связанные с окружностью.
Величина дуги окружности равна величине центрального угла, на неё опирающегося.
Вписанный угол равен половине угловой величины дуги, на которую он опирается.
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Угол между пересекающимися хордами равен полусумме противоположных дуг, высекаемых хордами.
Угол между двумя секущими, пересекающимися вне круга, равен полуразности дуг, высекаемых секущими на окружности.
Угол между касательной и хордой, проведённой из точки касания, равен половине угловой величины дуги, высекаемой на окружности этой хордой.
Свойства хорд окружностей.
Линия центров двух пересекающихся окружностей перпендикулярна их общей хорде.
Произведения длин отрезков хорд АВ и СD окружности, пересекающихся в точке Е, равны, то есть 
Вписанные и описанные окружности.
Центры вписанной и описанной окружностей правильного треугольника совпадают.
Центр окружности, описанной около прямоугольного треугольника,- середина гипотенузы.
Если в четырёхугольник можно вписать окружность, то суммы его противоположных сторон равны.
Если четырёхугольник можно вписать в окружность, то сумма его противоположных углов равна 
Если сумма противоположных углов четырёхугольника равна 
Если в трапецию можно вписать окружность, то боковая сторона трапеции видна из центра окружности под прямым углом.
Если в трапецию можно вписать окружность, то радиус окружности есть среднее пропорциональное отрезков, на которые точка касания делит боковую сторону.
Если в многоугольник можно вписать окружность, то его площадь равна произведению полупериметра многоугольника на радиус этой окружности.
Теорема о касательной и секущей и следствие из неё.
Если из одной точки проведены к окружности касательная и секущая, то произведение всей секущей на её внешнюю часть равна квадрату касательной.
Произведение всей секущей на её внешнюю часть для данной точки и данной окружности постоянно.
Длина окружности радиуса R равна 
Площадь круга радиуса R равна 
Площадь кругового сектора 
Геометрия 7-9 кл. Учебник для общеобразовательных учреждений. Москва «Просвещение» 2008г. Авторы: Л.С.Атанасян и др.
Математика 9 класс. Подготовка к ГИА-2012. Учебно — методическое пособие. Под редакцией Ф.Ф.Лысенко, С.Ю.Кулабухова. ЛЕГИОН-М Ростов-на-Дону 2011.
Математика. Сборник заданий. Подготовка к ГИА- 2012. Москва «эксмо» 2011. Авторы: В.В.Кочагин, М.Н.Кочагина.
🌟 Видео
Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

Параллельные прямые циркулемСкачать

6 .7 кл Построение параллельных прямых.Как построить параллельные прямыеСкачать

МЕРЗЛЯК 7 ГЕОМЕТРИЯ. СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ. ПАРАГРАФ-15Скачать

Параллельные прямые. 6 класс.Скачать

Задачи на доказательство по геометрии. Признаки параллельности прямых.Скачать

Задача, которую боятсяСкачать

7 класс, 28 урок, Аксиома параллельных прямыхСкачать

Урок 15 Свойства параллельных прямых (7 класс)Скачать

Геометрия 7 класс (Урок№21 - Свойства параллельных прямых.)Скачать

Геометрия 7 класс (Урок№20 - Аксиома параллельных прямых.)Скачать

УГЛЫ ПРИ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ И СЕКУЩЕЙСкачать

Параллельные прямые (задачи).Скачать

решение задач параллельные прямые, сумма углов треугольников, прямоугольные треугольникиСкачать

ОГЭ/БАЗА. Геометрия с нуля. Параллельные прямые, прямоугольный треугольникСкачать