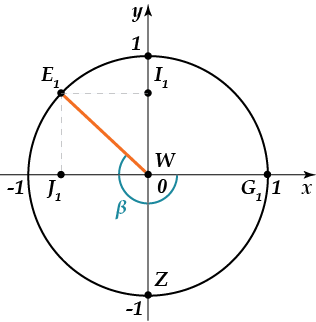Найти координаты точки окружности соответствующей углу (4 видео)

Тригонометрия

Найти координаты точки на единичной окружности, полученной поворотом точки ( Aleft( 1;0 right) ) на ( -225^circ ) .

Окружность единичная с центром в точке ( left( 0;0 right) ) , значит, мы можем воспользоваться упрощёнными формулами:

( beginx=cos beta =cos (-225^circ )\y=sin beta =sin (-225^circ )end ) .

Можно заметить, что ( -225^circ =-360^circ +135^circ ; -225^circ =-180^circ -45^circ ) . Изобразим рассматриваемый пример на рисунке:

Радиус ( <_>W ) образует с осью ( x ) углы, равные ( 45^circ ) и ( 135^circ ) . Зная, что табличные значения косинуса и синуса ( 45^circ ) равны ( displaystyle dfrac<sqrt> ) , и определив, что косинус здесь принимает отрицательное значение, а синус положительное, имеем:

Подробней подобные примеры разбираются при изучении формул приведения тригонометрических функций в теме «Формулы тригонометрии».

Таким образом, искомая точка имеет координаты ( left( -dfrac<sqrt>;dfrac<sqrt> right) ) .

Содержание

Тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела. Большое значение имеет техника триангуляции, позволяющая измерять расстояния до недалёких звёзд в астрономии, между ориентирами в географии, контр
«Управление общеобразовательной организацией: новые тенденции и современные технологии»
Описание презентации по отдельным слайдам:
Дистанционное обучение как современный формат преподавания
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Математика: теория и методика преподавания в образовательной организации
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
Дистанционные курсы для педагогов
Другие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Автор материала
Дистанционные курсы для педагогов
Подарочные сертификаты
10.V-3. Поворот точки вокруг начала координат-2
📹 Видео

Видео:Найти координаты точки единичной окружности полученной при повороте точки Ро(1;0) на угол π, 450°...Скачать

Тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела. Большое значение имеет техника триангуляции, позволяющая измерять расстояния до недалёких звёзд в астрономии, между ориентирами в географии, контр

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Тригонометрические Функции Поворот точки вокруг начала координат

Проверка домашнего задания 1. Какая фигура называется углом ? 2. В чем измеряются углы? 3. Какие углы бывают, примеры их величин? 4. Какой угол принимают за угол в 10 ? 5. Что такое угол в один радиан? 6. Каково соотношение между радианом и градусом? 7. Сколько радиан составляют 1800?

Проверочная работа 1800 = π

Ответы на проверочную работу Оценка за проверочную работу: 7-8 верных ответов — оценка «3» 9-10 верных ответов – оценка «4» 11-12 верных ответов – оценка «5»

Единичная окружность Окружность с центром в начале координат и радиусом равным 1 — называется единичной окружностью. О Р 1 1 -1 -1 точка Р — начало отсчета углов М α + α — α I четверть II четверть III четверть IV четверть -α

Единичная окружность Окружность с центром в начале координат и радиусом равным 1 — называется единичной окружностью. О Р точка Р — начало отсчета углов + α — α I четверть II четверть III четверть IV четверть α = 00 α = 900 α = 1800 α = 2700 α = 3600

Единичная окружность Окружность с центром в начале координат и радиусом равным 1 — называется единичной окружностью. О Р точка Р — начало отсчета углов — α I четверть II четверть III четверть IV четверть α = 00 α = -900 α = -1800 α = -2700 α = 3600

Единичная окружность точка Р — начало отсчета углов Задание устно: Определить четверть ,в которой лежит угол 125 0 -45 0 — 300 0 -250 0 -150 0 2100 3300 3900 4600 -1200 Р π 12 3π 4 7π 4 7π 8

Координаты точки на единичной окружности О Р (1;0) I четверть II четверть III четверть IV четверть 00 900 = 1800 = 2700 = 3600= А (0;1) В (-1;0) С (0;-1) Точке А (0,1) соответствую углы: 900 900+3600 900+3600 +3600 +… 900-3600 900-3600 -3600 -… Или в радианах:

Координаты точки на единичной окружности О Р (1;0) 00 900 = 1800 = 2700 = 3600= А (0;1) В (-1;0) С (0;-1) 1. Каждому углу соответствует единственная точка на окружности 2. Одной и той же точке на окружности соответствует бесконечное множество углов где к – целое число М

Самостоятельная работа Найти координаты точки окружности, соответствующей углу: Записать все углы в радианах, соответствующие точке на окружности с координатами: 6. (0;-1) 7. (1;0) Найти координаты точки окружности, соответствующей углу: Записать все углы, соответствующие точке на окружности с координатами: 6. (-1;0) 7. (0;1) Вариант 2 Вариант 1

Ответы на проверочную работу Сегодня на уроке я узнал….. Сегодня на уроке я познакомился……. Сегодня на уроке я повторил……. Сегодня на уроке я научился……… Д/З: §22 стр.123 № 420

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Сейчас обучается 942 человека из 80 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Сейчас обучается 315 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Сейчас обучается 694 человека из 75 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 479 804 материала в базе

Видео:Как искать точки на тригонометрической окружности.Скачать

Дистанционные курсы для педагогов

Другие материалы

29.12.2015
722

29.12.2015
3542

29.12.2015
1078

29.12.2015
708

29.12.2015
533

29.12.2015
2109

29.12.2015
934

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

29.12.2015 2165 —> —> —> —>
PPTX 396.5 кбайт —> —>
Оцените материал:

Настоящий материал опубликован пользователем Балкарова Наталья Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

На проекте: 6 лет
Подписчики: 0
Всего просмотров: 33051
Всего материалов: 24

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Точки, полученные поворотом точки Р (1; 0) вокруг начала координат на заданные углыСкачать

Дистанционные курсы
для педагогов

548 курсов от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

В Китае приняли закон о сокращении нагрузки на школьников

Время чтения: 1 минута

В России утвердили новые правила аккредитации образовательных учреждений

Время чтения: 1 минута

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Стартовал региональный этап Всероссийской олимпиады школьников

Время чтения: 2 минуты

Пандемия позволила детям получить больше внимания со стороны родителей

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Алгебра 10 класс. 20 сентября. Числовая окружность #6 координаты точекСкачать

10.V-3. Поворот точки вокруг начала координат-2

Алгебра. 10 класс. Тригонометрия. Тест 3.

Вариант 1.

1. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол 3π/2±π.

A) (0; -1); B) (0; 1); C) (1; 0); D) (-1; 0).

2. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол π/6±π.

3. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол π+πk, где kϵZ.

A) (-1; 0); (1; 0); B) (0; -1); (1; 0); C) (1; 0); (0; 1); D) (0; -1); (-1; 0).

4. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получить

A) 3π/4+2πk, kϵZ; B) -π/4+2πk, kϵZ; C) π/4+2πk, kϵZ; D) 7π/4+2πk, kϵZ.

5. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получались

A) π/6+πk, kϵZ; B) π/3+2πk, kϵZ; C) -π/3+πk, kϵZ; D) -π/6+2πk, kϵZ.

6. При повороте точки Р(1; 0) вокруг начала координат получены углы α=π/2+πk, kϵZ. Записать те из них, которые принадлежат отрезку [-5π; -7π/2].

A) -9π/2; -4π; B) -9π/2; -7π/2; C) -7π/2; D) -5π; -9π/2.

7. Точке М единичной окружности соответствует бесконечное множество действительных чисел ±5π/6+2πk, где kϵZ. Записать те из них, которые принадлежат отрезку [3π; 9π/2].

A) 19π/6; B) 17π/6; C) 4π; D) 13π/6.

8. Точке М единичной окружности соответствует бесконечное множество действительных чисел ±π/3+πk, где kϵZ. Записать те из них, которые принадлежат отрезку [-2π; -π/2].

A) -5π/3; -4π/3; B) -4π/3; -2π/3; C) -5π/3; -4π/3; -2π/3; D) -2π; -4π/3; -2π/3.

Вариант 2.

1. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол π/2±π.

A) (0; -1); B) (0; 1); C) (1; 0); D) (-1; 0).

2. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол π/3±π.

3. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол -π+πk, где kϵZ.

A) (-1; 0); (0; -1); B) (0; -1); (1; 0); C) (1; 0); (0; 1); D) (1; 0); (-1; 0).

4. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получить

A) 5π/6+2πk, kϵZ; B) π/6+2πk, kϵZ; C) -π/6+2πk, kϵZ; D) 5π/3+2πk, kϵZ.

5. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получались

A) -π/4+πk, kϵZ; B) π/4+πk, kϵZ; C) -π/8+πk, kϵZ; D) -π/6+2πk, kϵZ.

6. При повороте точки Р(1; 0) вокруг начала координат получены углы α=πk, kϵZ. Записать те из них, которые принадлежат отрезку [4π; 11π/2].

A) 9π/2; 5π; B) 4π; 9π/2; C) 4π; 5π; D) 5π.

7. Точке М единичной окружности соответствует бесконечное множество действительных чисел -π/4+2πk, где kϵZ. Записать те из них, которые принадлежат отрезку [-9π/2; -3π].

A) -13π/4; B) -19π/4; C) -15π/4; D) -17π/4.

8. Точке М единичной окружности соответствует бесконечное множество действительных чисел ±2π/3+2πk, где kϵZ. Записать те из них, которые принадлежат отрезку [-5π; -7π/2].

A) -16π/3; B) -14π/3; C) -13π/3; D) -3π; -14π/3.

Вариант 3.

1. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол -π/2±π.

A) (0; 1); B) (0; -1); C) (1; 0); D) (-1; 0).

2. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол 3π/4±π.

3. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол -3π/2+πk, где kϵZ.

A) (-1; 0); (0; -1); B) (0; 1); (0; -1); C) (1; 0); (0; 1); D) (1; 0); (-1; 0).

4. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получить

A) 5π/3+2πk, kϵZ; B) π/3+2πk, kϵZ; C) π/6+2πk, kϵZ; D) 7π/6+2πk, kϵZ.

5. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получались

A) -π/6+πk, kϵZ; B) -π/4+πk, kϵZ; C) -π/3+πk, kϵZ; D) π/6+2πk, kϵZ.

6. При повороте точки Р(1; 0) вокруг начала координат получены углы α=5π/6+2πk, kϵZ. Записать те из них, которые принадлежат отрезку [-6π; -4π].

A) -5π; B) -29π/6; C) -25π/6; D) -31π/6.

7. Точке М единичной окружности соответствует бесконечное множество действительных чисел ±π/4+2πk, где kϵZ. Записать те из них, которые принадлежат отрезку [-5π; -3π].

A) -17π/4; B) -15π/4; C) -15π/4; -17π/4; D) -13π/4; -15π/4.

8. Точке М единичной окружности соответствует бесконечное множество действительных чисел π/4+πk/2, где kϵZ. Записать те из них, которые принадлежат отрезку [5π; 13π/2].

A) 21π/4; 23π/4; 25π/4; B) 21π/4; 23π/4; C) 23π/4; 25π/4; D) 23π/4.

Вариант 4.

1. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол -3π/2±π.

A) (-1; 0); B) (0; 1); C) (1; 0); D) (0; -1).

2. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол 5π/6±π.

3. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол 3π/2+πk, где kϵZ.

A) (-1; 0); (0; -1); B) (0; -1); (0; 1); C) (1; 0); (0; 1); D) (1; 0); (-1; 0).

4. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получить

A) π/3+2πk, kϵZ; B) -π/3+2πk, kϵZ; C) 2π/3+2πk, kϵZ; D) π/6+2πk, kϵZ.

5. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получались

A) π/6+πk, kϵZ; B) -π/4+πk, kϵZ; C) π/3+πk, kϵZ; D) π/4+πk, kϵZ.

6. При повороте точки Р(1; 0) вокруг начала координат получены углы α=π/3+2πk, kϵZ. Записать те из них, которые принадлежат отрезку [-5π/2; -π].

A) -5π/3; B) -π/3; -4π/3; C) -2π/3; D) -4π/3.

7. Точке М единичной окружности соответствует бесконечное множество действительных чисел ±π/3+2πk, где kϵZ. Записать те из них, которые принадлежат отрезку [-2π; -π/2].

A) -π/3; B) -2π/3; C) -4π/3; D) -5π/3.

8. Точке М единичной окружности соответствует бесконечное множество действительных чисел π/4+πk/2, где kϵZ. Записать те из них, которые принадлежат отрезку [-7π/2; -5π/2].

A) -13π/4; B) -13π/4; -11π/4; C) -11π/4; D) -3π.