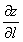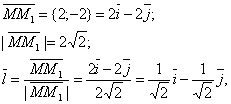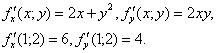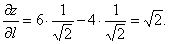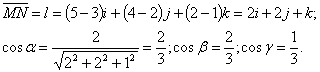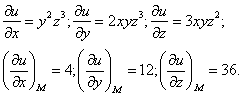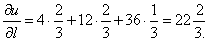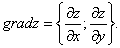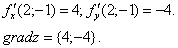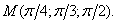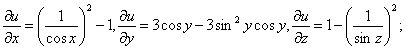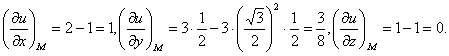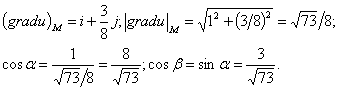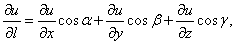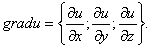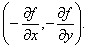Найти градиент функции в точке построить вектор (8 видео)

Градиент функции онлайн

Градиент функции — это вектор координатами которого являются частные производные этой функции по всем её переменным.

Градиент обозначается символом набла . Выражение градиента некоторой функции записывается следующим образом:

где , , — частные производные функции по переменным , , соответственно.

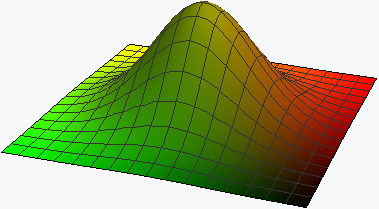
Вектор градиента указывает направление наискорейшего роста функции. Рассмотрим график функции .

Эта функция достигает своего единственного максимума в точке . График градиентного поля данной функции имеет вид:

Из данного градика видно, что в каждой точке вектор градиента направлен в сторону наискорейшего роста функции, т.е. в точку . При этом модуль вектора отражает скорость роста (крутизну подъёма) функции в этом направлении.

Задача вычисления градиента функции очень часто возникает при поиске эстремумов функции с использованием различных численных методов.

Наш онлайн калькулятор позволяет вычислить градиент практически любой функции как общем виде, так и в конкретной точке с описанием подробного хода решения на русском языке.

Содержание

5.6. Производная по направлению. Градиент. Линии уровня функции
Производная по направлению, градиент функции: объяснение, примеры
Понятие производной по направлению
Примеры нахождения производной по направлению
Градиент функции
📺 Видео

Видео:Нахождение градиента функции в точкеСкачать

5.6. Производная по направлению. Градиент. Линии уровня функции

Определение. Предел отношения 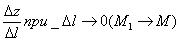, если он существует, называется Производной функции Z=F(M) в точке M(X; Y) по направлению вектора L .

Обозначение.

Если функция F(M) дифференцируема в точке М(х; у), то в точке М(х; у) существует производная по любому направлению L, исходящему из М; вычисляется она по следующей формуле:

(8)

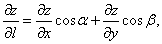
Где Cos И Cos — направляющие косинусы вектора L.

Пример 46. Вычислить производную функции Z=X2+Y2X в точке М(1; 2) по направлению вектора ММ1, где М1 – точка с координатами (3; 0).

Решение. Найдем единичный вектор L, имеющий данное направление:

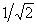
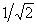
Откуда Cos=; Cos=-.

Вычислим частные производные функции в точке М(1; 2):

По формуле (8) получим

Пример 47. Найти производную функции U = Xy2Z3 в точке М(3; 2; 1) В направлении вектора MN, где N(5; 4; 2).

Решение. Найдем вектор 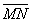и его направляющие косинусы:

Вычислим значения частных производных в точке М:

Следовательно,

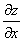
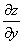
Определение. Градиентом Функции Z=F(M) в точке М(х; у) называется вектор, координаты которого равны соответствующим частным производным и, взятым в точке М(х; у).

Обозначение.

Решение. Находим частные производные: 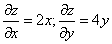и их значения в точке М(2; -1):

Пример 49. Найти величину и направление градиента функции 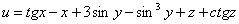в точке

Решение. Найдем частные производные и вычислим их значения в точке М:

Аналогично определяется производная по направлению для функции трех переменных U=F(X, Y, Z), выводятся формулы

Вводится понятие градиента

Подчеркнем, что Основные свойства градиента функции важнее для анализа экономических оптимизационных задач: в направлении градиента функция возрастает. В экономических задачах находят применение следующие свойства градиента:

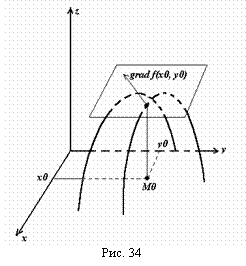
1) Пусть задана функция Z=F(X, Y), имеющая частные производные в области определения. Рассмотрим некоторую точку М0(х0, у0) из области определения. Значение функции в этой точке пусть равно F(X0, Y0). Рассмотрим график функции. Через точку (X0, Y0, F(X0, Y0)) трехмерного пространства проведем плоскость, касательную к поверхности графика функции. Тогда градиент функции, вычисленный в точке (х0, у0), рассматриваемый геометрически как вектор, приложенный в точке (X0, Y0, F(X0, Y0)), будет перпендикулярен касательной плоскости. Геометрическая иллюстрация приведена на рис. 34.

2) Градиент функции F(X, Y) в точке М0(х0, у0) указывает направление наиболее быстрого возрастания функции в точке М0. Кроме того, любое направление, составляющее с градиентом острый угол, является направлением роста функции в точке М0. Другими словами, малое движение из точки (х0, у0) по направлению градиента функции в этой точке ведет к росту функции, причем в наибольшей степени.

Рассмотрим вектор, противоположный градиенту. Он называется Антиградиентом. Координаты этого вектора равны:

Антиградиент функции F(X, Y) в точке М0(х0, у0) указывает направление наиболее быстрого убывания функции в точке М0. Любое направление, образующее острый угол с антиградиентом, является направлением убывания функции в этой точке.

3) При исследовании функции часто возникает необходимость нахождения таких пар (х, у) из области определения функции, при которых функция принимает одинаковые значения. Рассмотрим множество точек (X, Y) из области определения функции F(X, Y), таких, что F(X, Y)=Const, где запись “Const” означает, что значение функции зафиксировано и равно некоторому числу из области значений функции.

Линии уровня геометрически изображаются на плоскости изменения независимых переменных в виде кривых линий. Получение линий уровня можно представить себе следующим образом. Рассмотрим множество С, которое состоит из точек трехмерного пространства с координатами (X, Y, F(X, Y)=Const), которые, с одной стороны, принадлежат графику функции Z=F(X, Y), с другой — лежат в плоскости, параллельной координатной плоскости ХОУ, и отстоящей от неё на величину, равную заданной константе. Тогда для построения линии уровня достаточно поверхность графика функции пересечь плоскостью Z=Const и линию пересечения спроектировать на плоскость ХОУ. Проведенное рассуждение является обоснованием возможности непосредственно строить линии уровня на плоскости ХОУ.

Определение. Множество линий уровня называют Картой линий уровня.

Хорошо известны примеры линий уровня – уровни одинаковых высот на топографической карте и линии одинакового барометрического давления на карте погоды.

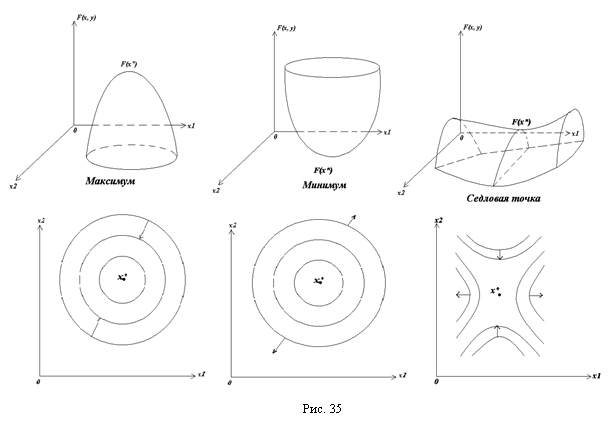
Определение. Направление, вдоль которого скорость увеличения функции максимальна, называется «предпочтительным» направлением, или Направлением наискорейшего роста.

«Предпочтительное» направление задается вектором-градиентом функции. На рис. 35 изображены максимум, минимум и седловая точка в задаче оптимизации функции двух переменных при отсутствии ограничений. В нижней части рисунка изображены линии уровня и направления наискорейшего роста.

Решение. Уравнение семейства линий уровня имеет вид X2+Y2=C (C>0). Придавая С различные действительные значения, получим концентрические окружности с центром в начале координат.

Построение линий уровня. Их анализ находит широкое применение в экономических задачах микро — и макроуровня, теории равновесия и эффективных решений. Изокосты, изокванты, кривые безразличия – это все линии уровня, построенные для разных экономических функций.

Пример 51. Рассмотрим следующую экономическую ситуацию. Пусть производство продукции описывается Функцией Кобба-Дугласа F(X, Y)=10х1/3у2/3, где Х – количество труда, У – количество капитала. На приобретение ресурсов выделено 30 у. ед., цена труда составляет 5 у. ед., капитала – 10 у. ед. Зададимся вопросом: какой наибольший выпуск можно получить в данных условиях? Здесь под «данными условиями» имеются в виду заданные технологии, цены на ресурсы, вид производственной функции. Как уже отмечалось, функция Кобба-Дугласа является монотонно возрастающей по каждой переменной, т. е. увеличение каждого вида ресурса ведет к росту выпуска. В данных условиях ясно, что увеличивать приобретение ресурсов можно до тех пор, пока хватает денег. Наборы ресурсов, стоимость которых составляет 30 у. ед., удовлетворяют условию:

Т. е. определяют линию уровня функции:

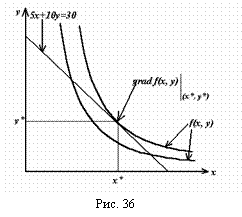
С другой стороны, с помощью линий уровня Функции Кобба-Дугласа (рис. 36) можно показать возрастание функции: в любой точке линии уровня направление градиента – это направление наибольшего возрастания, а для построения градиента в точке достаточно провести касательную к линии уровня в этой точке, построить перпендикуляр к касательной и указать направление градиента. Из рис. 36 видно, что движение линии уровня функции Кобба-Дугласа вдоль градиента следует производить до тех пор, пока она не станет касательной к линии уровня 5х + 10у = 30. Таким образом, с помощью понятий линии уровня, градиента, свойств градиента можно выработать подходы к наилучшему использованию ресурсов с точки зрения увеличения объемов выпускаемой продукции.

Видео:Математика без Ху!ни. Частные производные функции нескольких переменных. Градиент.Скачать

Производная по направлению, градиент функции: объяснение, примеры

Видео:Градиент в точке.Скачать

Понятие производной по направлению

Понятие производной по направлению рассматривается для функций двух и трёх переменных. Чтобы понять смысл производной по направлению, нужно сравнить производные по определению

Рассматривая функцию одной переменной, мы выяснили, что на оси Oy отображается приращение функции f(x) , соответствующее приращению аргумента x . Если мы имеем дело с функцией трёх переменных, то приращения аргументов x , y , z отображаются на осях Оx , Оy , Оz . Сам собой напрашивается вопрос: а где можно отобразить приращение уже не аргументов, а функции трёх переменных?

И вот ответ на этот вопрос: приращение функции трёх переменных отображается на некоторой прямой, направление которой определяется вектором, произвольно заданным в задаче.

Если рассматривается функция двух или трёх переменных, то два или три измерения задают аргументы, а упомянутая прямая, на которой отображается приращение функции, — это ещё одно измерение и для его акцентирования назовём это измерение не третьим или четвёртым, а нулевым, следуя программистской традиции (в программировании отсчёт чаще начинается не с единицы, а с нуля).

Для того, чтобы перейти к строгому математическому определению производной по направлению, нужно рассмотреть:

1) функцию u = f(M) , определённую в окрестности точки M с координатами x , y , z ;

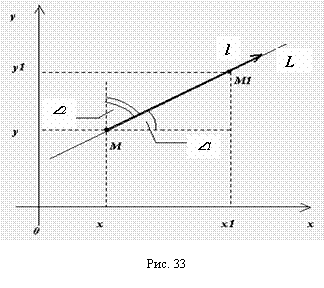
Через точку M проводим прямую, одно из двух возможных направлений которых совпадает с направлением вектора l . На получившейся прямой отметим точку M 1 , координаты которой образуют суммы координат точки M и приращений соответствующих аргументов функции трёх переменных:

Величину отрезка MM 1 можно обозначить .

Функция u = f(M) при этом получит приращение

Определение производной по направлению. Предел отношения при , если он существует, называется производной функции u = f(M) по направлению вектора l и обозначается , то есть

Формула, которой нужно пользоваться для нахождения производной по направлению, следующая:

Смысл этой формулы: производная по направлению является линейной комбинацией частных производных, причём направляющие косинусы показывают вклад в производную по направлению соответствующей частной производной.

Видео:10. ФНП. Градиент и производная по направлению функции двух переменных.Скачать

Примеры нахождения производной по направлению

Пример 1. Найти производную функции в точке M 0 (1; 2; 3) по направлению вектора .

Найдём направляющие косинусы, пользуясь определением скалярного произведения векторов:

Теперь можем найти производную по направлению данной функции по её формуле:

А сейчас — домашнее задание. В нём дана функция не трёх, а лишь двух переменных, но несколько иначе задан направляющий вектор. Так что придётся вновь повторить векторную алгебру.

Пример 2. Найти производную функции в точке M 0 (1; 2) по направлению вектора , где M 1 — точка с координатами (3; 0) .

Вектор, задающий направление производной, может быть дан и в такой форме, как в следующем примере — в виде разложения по ортам координатных осей, но эта хорошо знакомая тема из самого начала векторной алгебры.

Пример 3. Найти производную функции в точке M 0 (1; 1; 1) по направлению вектора .

Решение. Найдём направляющие косинусы вектора

Найдём частные производные функции в точке M 0 :

Следовательно, можем найти производную по направлению данной функции по её формуле:

Видео:Вектор-градиент (теория)Скачать

Градиент функции

Градиент функции нескольких переменных в точке M 0 характеризует направление максимального роста этой функции в точке M 0 и величину этого максимального роста.

Как найти градиент?

Нужно определить вектор, проекциями которого на оси координат являются значения частных производных , , этой функции в соответствующей точке:

То есть, должно получиться представление вектора по ортам координатных осей, в котором на каждый орт умножается соответствующая его оси частная производная.

Для градиента функции двух переменных формула короче: