Практически для решения задач на плоскости достаточно трех уравнений равновесия. В каждом конкретном случае используются уравнения с одним неизвестным.
Для разных случаев используются три группы уравнений равновесия.
Для частного случая, если уравновешена система параллельных сил, можно составить только два уравнения равновесия:
Ось Ох системы координат параллельна линии действия сил.
Примеры решения задач
Пример 1. Найти момент присоединенной пары при переносе силы F3 в точку В (рис. 5.3).F1 = 10кН;F2 = 15кН; F3 = 18кН; а = 0,2 м.
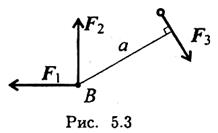
Решение
Используем теорему Пуансо.
Пример 2. Найти главный вектор системы (рис. 5.4). F1 = 10кН; F2 = 16кН;F3= 12кН;т = 60кН-м.
Решение
Главный вектор равен геометрической сумме сил:
 |
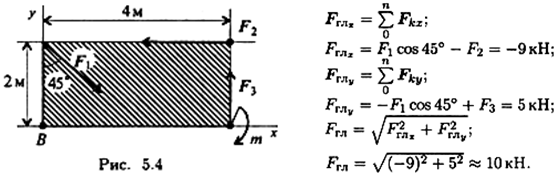Пример 3. Найти главный момент системы относительно точки В (использовать данные примера 2).
Решение
Главный момент равен алгебраической сумме моментов сил относительно точки приведения:
Пример 4. К телу приложена уравновешенная система сил (рис. 5.5). Две из них неизвестны. Определить неизвестные силы.
Решение
 |
Наносим оси координат и используем уравнения равновесия:
Пример 5. К двум точкам тела приложены четыре силы F1 = F2 = F3 = F4 = 5 Н, как показано на рис. 1.46, а. Привести эти силы к точке А, а затем найти их равнодействующую.
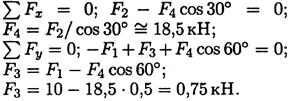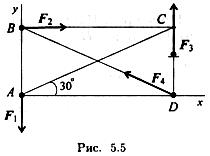
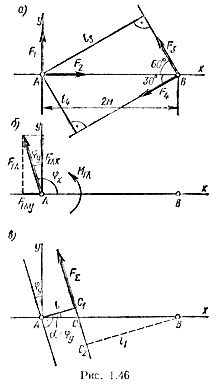
Решение
1. Центр приведения (точка А) задан. Поэтому примем точку А за начало координат и проведем ось х вдоль отрезка АВ, а ось у — по линии действия силы F1 (рис. 1.46, а).
Отсюда проекция на ось х главного вектора
3.Определим проекции сил на ось у:
Отсюда проекция на ось у главного вектора
Для большей наглядности и облегчения дальнейшего решения задачи целесообразно найденные проекции Fгл х и Fгл у главного вектора отложить вдоль осей координат (рис. 1.46, б).
4. Из формулы (1,27) определим модуль главного вектора:
5. Находим угол 
По таблицам или с помощью счетной логарифмической линейки определяем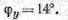 
Из рис. 1.46, б следует, что 
6. Определяем главный момент, как алгебраическую сумму моментов данных сил относительно точки А МА(F1) = 0 и МА(F2) = 0, так как линия действия сил F1 и F2 проходит через точку А (центр приведения);
Главный момент MГЛ > 0, значит он действует против хода часовой стрелки (рис. 1.46, б).
Равнодействующая FΣ = Fгл и линия ее действия, параллельная главному вектору, проходит от центра приведения А на расстоянии
Линия действия равнодействующей пересекает ось х в точке С и отсекает отрезок
Таким образом, равнодействующая заданной на рис. 1.46, а системы сил FΣ = 7,07 Н, линия ее действия образует с выбранными осями координат углы φх = 104°, φу =14° и пересекает отрезок АВ в точке С на расстоянии АС = 54 см.
Тот же результат был бы получен при выборе за центр приведения точки В, но в этом случае получилось бы ВС2 = 1,42 м и BС
146 см (рис, 1,46, б). Проверьте: так ли это.
Контрольные вопросы и задания
1. Чему равен главный вектор системы сил?
2. Чему равен главный момент системы сил при приведении ее к точке?
3. Чем отличается главный вектор от равнодействующей плоской системы произвольно расположенных сил?
Выбрать из предложенных ответов:
· величиной и направлением;
4. Тело движется равномерно и прямолинейно (равновесие). Чему равны главный вектор и главный момент системы?
5. Тело вращается вокруг неподвижной оси. Чему равны главный вектор и главный момент действующей на него системы сил?
 |
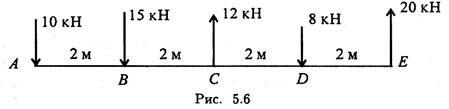6. Найдите главный вектор и главный момент системы сил, если центр приведения находится в точке А (рис. 5.6).
7. Какое еще уравнение равновесия нужно составить, чтобы убедиться в том, что система сил (рис. 5.7) находится в равновесии?
Видео:§4.3. Главный вектор и главный момент сил инерцииСкачать
ТЕХ.МЕХ.. Методическое пособие по дисциплине Техническая механика рекомендовано для специальности Сварочное производство
| Название | Методическое пособие по дисциплине Техническая механика рекомендовано для специальности Сварочное производство |
| Анкор | ТЕХ.МЕХ..doc |
| Дата | 31.01.2017 |
| Размер | 2.01 Mb. |
| Формат файла |  |
| Имя файла | ТЕХ.МЕХ..doc |
| Тип | Методическое пособие #1432 |
| страница | 4 из 8 |
| Подборка по базе: Лекции по дисциплине _Тестирование информационных систем_ (2).do, методическое пособие_наращивание волос.docx, Практическое задание по дисциплине Предпринимательство.docx, Практическое задание по дисциплине Маркетинг.docx, Стандартизация, подтв. соответствия Методич. пособие.docx, Практическая работа по дисциплине Римское право.docx, Характеристика ЭУМК по дисциплине.docx, Практическое задание по дисциплине Финансовый менеджмент.docx, Практическое задание по дисциплине Организация инновационной дея, Вопросы к экзамену по дисциплине.docx Тема 1.4. Плоская система произвольно расположенных сил. Уметь приводить произвольную плоскую систему сил к точке, определяя величины главного вектора и главного момента системы. Знать три формы уравнений равновесия и уметь ими пользоваться при определении реакций в опорах балочных систем. Виды опор балок и их реакции (рис. П2.1)
Условия равновесия
Упражнения при подготовке к самостоятельной работе
F = 20кН; АВ = 6м; ВС = 2м.
2. Система сил находится в равновесии. Определить величину момента пары m (рис. П2.5).
3. Нанести реакции в опорах балок 1 и 2 (рис. П2.6).
4. Определить величину реакции в опоре А. Приложена распределенная нагрузка интенсивностью q = 5 кH/м (рис. П2.7).
Определение величин реакции в опорах балочных систем под действием сосредоточенных и распределенных нагрузок Задание 3. Определить величины реакций в шарнирных опорах балки. Провести проверку правильности решения.
ТЕСТ ДЛЯ САМОКОНТРОЛЯ: Произвольная плоская система сил.
Тема 1.6. Центр тяжести. Уметь определять положение Центра тяжести сложных геометрических фигур, определять положение Центра тяжести фигур, составленных из стандартных профилей. Центры тяжести простейших сечении (рис. П3.1) Геометрические характеристики стандартных прокатных профилей в задачниках или учебниках по «Технической механике». 2) метод разделения на простые части; 3) метод отрицательных площадей.
где Ak — площади частей сечения; Xk; Yk — координаты ЦТ частей сечения; А — суммарная площаль сечения,
Упражнения при подготовке к самостоятельной работе 2. Определить координату Xc изображенного сечения (рис. П3.3). 3амечание. Сечение расчленить на три части.
3. Сколько координат центра тяжести нужно определять расчетным путем для каждого из изображенных сечений (рис. П3.4)? 4. По таблицам ГОСТ определить необходимые параметры сечений (рис. П3.5).
5. Определить координату Уc фигуры (рис. П3.5). 6. Какая характеристика сечения определяется по указанной формуле?
Задание 4. Определить координаты центра тяжести составного сечения. Сечения состоят из листов с поперечными размерами а×δ и прокатных профилей по ГОСТ 8239 – 89 и ГОСТ 8509 – 86. Уголок выбирается наименьшей толщины. Видео:Приведение системы сил к простейшему видуСкачать  Система сил. Главный вектор системы сил.Системой сил = (Рис.4).называется множество сил, приложенных к точкам механической системы. Главным вектором системы сил называется векторная сумма всех сил системы: Найти главный вектор можно, построив в произвольном центре О векторный многоугольник, в котором начало последующей силы совпадает с концом предыдущей (рис.4). Замыкающая сторона многоугольника и есть главный вектор V системы сил.
Для пространственной системы сил построить многоугольник практически трудно. Проще найти главный вектор аналитически. Проектируя слагаемые формулу (6) на оси координат, определим проекции главного вектора, его модуль и направляющие косинусы: Vx=Fkx; Vy=Fky; Vz=Fkz (7) V2=Vx2+Vy2+Vz2; Cos(V,x)=Vx/V; Cos(V,y)=Vy/V; Cos(V,z)=Vz/V Момент силы относительно точки. Теоремы о моменте Пусть сила F приложена в точке А тела, имеющей радиус-вектор r относительно центра О. Моментом силы F относительно центра О называется вектор
Направление векторного произведения усдовно и зависит от ориентированности пространства. Ориентированность пространства- это принятое нами правило соответствия прямой и дуговой стрелок: правого или левого винта. Вектора, направление которых зависит от оринтированности пространства, называются аксиальными. Важно, что для них (Рис.5) дуговая стрелка составляет физическую сущность (показывает направление вращения) а направление самого вектора условено. Мы будем работать в право ориентированном пространстве и направление векторного произведения всегда будем определять пл правилу правого винта: с конца mo видно , что сила стремится повернуть тело против часовой стрелки. Модуль момента равен произведению модуля силы на плечо h -длину перпендикуляра, опущенного из центра О на линию действия силы. Очевидно, что момент силы тем меньше, чем меньше ее плечо, и он обращается в ноль для любого центра на линии действия силы. Вы это ощущаете, поднимая воротом ведро из колодца, и поэтому стараетесь приложить силу руки так, чтобы создать большее плечо. Из формулы для модуля момента ясно, что момент силы равен нулю только относительно точки, лежащей на линии действия силы. Теорема 1. О зависимости момента от центра
Рис.6 а) в общем случае момент силы зависит от центра б) перенос центра параллельно линии действия силы не изменяет момента Найдем связь между моментами силы F относительно центров А и В. Из Рис.6 ясно, что rA= AB+rB mA(F)=rAxF=(AB+rB)xF= rBxF +ABxF Теорема 2. О проекциях моментов. Проектируя (10) на ось z, проходящую через А и В, находим
Таким образом приходим к лемме: поскольку произведение АВ Х F перпендикулярно АВ и его проекция на z равна нулю. Проекции моментов силы относительно всех точек одной оси на эту ось равны между собой. Таким образом проекция моментов на ось характеризует действие силы по отношению к этой оси, поэтому называется моментом сил относительно. Матричное вычисление векторного произведения (момента). Присоединенная матрица. Известно, что векторное произведение можно представить в виде определителя матрицы
c=a x b == (aFz-zFy)i+(zFx-xFz)j+(xFy-yFx)k (12)
mo(F)=r x F== (yFz-zFy)i+(zFx-xFz)j+(xFy-yFx)k Здесь i, j, k — орты осей x, y, z с началом в центре О, x, y, z — проекции радиуса-вектора r на эти оси. В матричной алгебре вектору соответствует столбец его проекций на декартовы оси. Таким образом вектор-столбец момента имеет вид
Легко убедится, что этот же результат можно получить, умножив кососимметричную матрицу, составленную из элементов столбца r
на вектор-столбец сил F (1). Матрица R называется присоединенной матрицей вектора r В общем случае столбец проекций векторного произведения c=a b удобно находить через присоединенную кососимметричную матрицу первого сомножителя часовой стрелки 💥 ВидеоТехническая механика/ Определение равнодействующей. Плоская система сходящихся сил.Скачать  Система сходящихся сил. Решение задач по МещерскомуСкачать  Определить реакции стержней, удерживающих груз весомСкачать  Термех. Статика. Приведение пространственной системы сил к центруСкачать  Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать  1 Решение задачи графическим и аналитическим методомСкачать  Решение "базисной системы векторов" (2)Скачать  Преобразование систем сил Часть 2Скачать  Определение реакций опор простой рамыСкачать  Видеоурок 1. Определение реакций жёстких стержней.Скачать  Момент силыСкачать  Статика. Плоская система сходящихся сил.Скачать  ОДИНОЧКА Книга 2 АУДИОКНИГА #попаданцы #аудиокниги #фантастикаСкачать  Определение опорных реакции в пространственной конструкции. ТермехСкачать  Термех. Статика. Расчётно-графическая работа по статике №2. Задание 1 и решениеСкачать  У Кремля снесло строительные леса , обрушившие зубцы (Скачать  Урок 107. Задачи на закон сохранения импульса (ч.1)Скачать  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
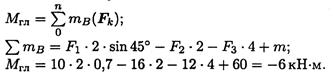
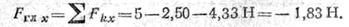
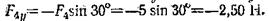
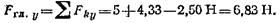
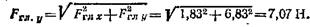
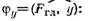
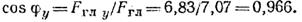
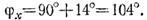
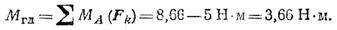
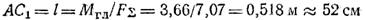
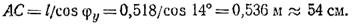
F, кН
l = 2кН,
