- Условие
- Найдите радиус окружности вписанной в треугольник 60
- Радиус вписанной в треугольник окружности онлайн
- 1. Радиус вписанной в треугольник окружности, если известна площадь и полупериметр треуольника
- 2. Радиус вписанной в треугольник окружности, если известны все три стороны треугольника
- 3. Радиус вписанной в треугольник окружности, если известны две стороны и угол между ними
- 4. Радиус вписанной в треугольник окружности, если известны сторона и прилежащие два угла
- Радиус вписанной окружности в треугольник
- Радиус вписанной окружности в любой треугольник
- Радиус вписанной окружности в правильный треугольник
- Радиус вписанной окружности в равнобедренный треугольник
- Радиус вписанной окружности в прямоугольный треугольник
- Найдите радиус окружности вписанной в треугольник 60
- Нахождение радиуса вписанной в треугольник окружности
- Формулы вычисления радиуса вписанной окружности
- Произвольный треугольник
- Прямоугольный треугольник
- Равнобедренный треугольник
- Равносторонний треугольник
- Примеры задач
- 📺 Видео
Условие
1.Найдите радиус окружности, вписанной в треугольник, если один из углов треугольника равен 60о, а расстояние от центра окружности до вершины этого угла равно 10.
2.Отрезки АВ и ВС являются соответственно диаметром и хордой окружности с центром О. Найдите угол АОС, если угол АВС равен 67градусов. Ответ дайте в градусах.
3.Окружность с центром О касается сторон угла с вершиной А в точках В и С. Найдите угол ВАС, если угол ВОС равен 127о. Ответ дайте в градусах.
4.Диагональ прямоугольника образует с одной из его сторон угол 11о. Найдите угол между прямыми, содержащими диагонали прямоугольника. Ответ дайте в градусах.
Видео:2062 найдите радиус окружности вписанной в правильный треугольник высота которого 132Скачать

Найдите радиус окружности вписанной в треугольник 60
Видео:Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

Радиус вписанной в треугольник окружности онлайн
С помощю этого онлайн калькулятора можно найти радиус вписанной в треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
| Открыть онлайн калькулятор |
Видео:Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать

1. Радиус вписанной в треугольник окружности, если известна площадь и полупериметр треуольника
Пусть известна площадь S треугольника и полупериметр
| ( small p=frac ) | (1) |
где a, b, c стороны треугольника (Рис.1).
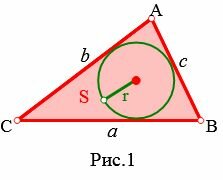 |
Найдем радиус вписанной в треугольник окружности r.
Из центра O вписанной в треугольник окружности проведем перпендикуляры к сторонам треугольника. Все эти перпендикуляры равны радиусу r вписанной в треугольник окружности (Рис.2).
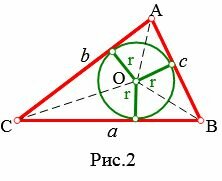 |
Прямыми OA, OB, OC разделим треугольник ABC на три треугольника: AOC, COB, AOB. Найдем площадь треугольников AOC, COB, AOB:
| ( small S_=frac cdot r cdot b ,) ( small S_=frac cdot r cdot c, ) ( small S_ =frac cdot r cdot a ) | (2) |
| ( small S=S_+S_+S_ )( small =frac cdot r cdot b ) ( small +frac cdot r cdot c ) ( small +frac cdot r cdot a ) ( small =frac cdot r cdot ( a+b+c) ) | (3) |
| ( small S=r cdot p. ) | (4) |
Найдем радиус r вписанной в треугольник окружности из равенства (4):
| ( small r=frac . ) | (5) |
Пример 1. Известны площадь ( small S=17 ) и полупериметр ( small p=10 ) треугольника. Найти радиус вписанной в треугольник окружности.
Решение. Для нахождения радиуса вписанной в треугольник окружности воспользуемся формулой (5).
Подставим значения ( small S=17 ) и ( small p=10 ) в (5):
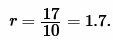 |
Ответ:
Видео:Формулы для радиуса окружности #shortsСкачать

2. Радиус вписанной в треугольник окружности, если известны все три стороны треугольника
Пусть известны три стороны треугольника: a, b, c. Найдем радиус вписанной в треугольник окружности (Рис.3).
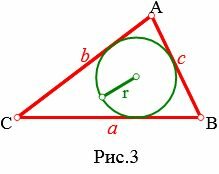 |
Площадь треугольника по трем сторонам вычисляется из формулы:
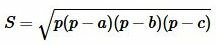 | (6) |
где полупериметр p вычисляется из формулы (1).
Подставляя (6) в (5), получим формулу радиуса вписанной в треугольник окружности:
| ( small r=sqrt >, ) | (7) |
Пример 2. Известны стороны треугольника: ( small a=15 ,; b=7, ; c=9.) Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанный в треугольник найдем сначала полупериметр треугольника из формулы (1):
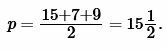 |
Подставим значения ( small a,; b, ; c, ; p ) в (7):
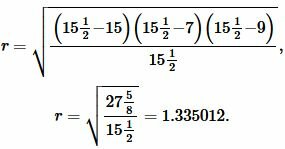 |
Ответ:
Видео:Окружность вписана в равносторонний треугольник, найти радиусСкачать

3. Радиус вписанной в треугольник окружности, если известны две стороны и угол между ними
Пусть известны стороны b и c треугольника и угол A между ними (Рис.4). Найдем формулу радиуса вписанной в треугольник окружности.
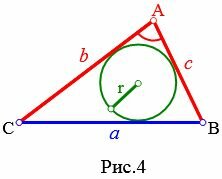 |
Из теоремы косинусов найдем сторону a треугольника:
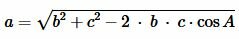 | (8) |
Далее, для вычисления радиуса вписанной в треугольник окружности, воспользуемся формулой (7), где полупериметр p вычисляется из (1).
Пример 3. Известны стороны треугольника: ( small b=9 ,; c=7, ; ) и угол меджу ними A=30°. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанный в треугольник найдем сначала сторону a треугольника из формулы (8):
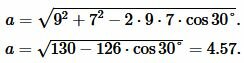 |
Далее найдем p из формулы (1):
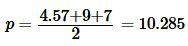 |
Подставим значения ( small a,; b, ; c, ; p ) в (7):
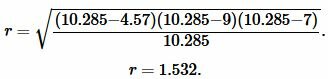 |
Ответ:
Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

4. Радиус вписанной в треугольник окружности, если известны сторона и прилежащие два угла
Пусть известны сторона a треугольника и прилежащие два угла B и C (Рис.5). Найдем радиус вписанной в треугольник окружности.
 |
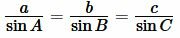 |
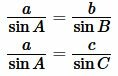 |
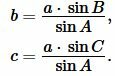 | (9) |
Поскольку сумма углов треугольника равна 180°, то имеем ( small angle A=180°-(angle B+angle C). ) Из формул приведения тригонометрических функций имеем: ( small sin A=sin (180°-( B+ C)) ) ( small =sin (B+C). ) Тогда формулы (9) можно переписать так:
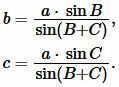 | (10) |
Получая значения сторон b, c из (10) и значение p из (1), можно найди радиус вписанной в треугольник окружности из формулы (7). Таким образом, для нахождения радиуса вписанной в треугольник окружности через сторону и прилежащим двум углам применяется формула
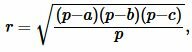 | (11) |
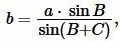 | (12) |
 , , | (13) |
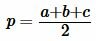 . . | (14) |
Пример 4. Сторона треугольника равена: ( small a=7 ,) а прилежащие два угла равны соответственно ( small angle B=25°, ) ( small angle C=40°, ) Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (11). Найдем, сначала, стороны b и c из формул (12),(13). Подставим значения ( small a=7 ,) ( small angle B=25°, ) ( small angle C=40°, ) в (12) и (13):
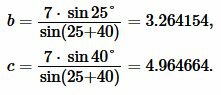 . . |
Далее найдем полупериметр p из формулы (14):
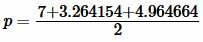 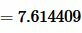 . . |
Подставляя значения a, b, c, p в (11), получим:
 |
Ответ:
Видео:Задача 6 №27910 ЕГЭ по математике. Урок 130Скачать

Радиус вписанной окружности в треугольник
Радиус вписанной в треугольник окружности
рассчитать и выразить через периметр, площадь,
высоту, основание, стороны, диаметр. Формулы
радиуса окружности вписанной в треугольник.
Центр вписанной в треугольник окружности — это одна
из замечательных точек треугольника, она расположена
в точке пересечения биссектрис треугольника, её
иногда называют инцентром.
Центр вписанной окружности правильного треугольника — это
точка, где пересекаются высоты, медианы и биссектрисы.
В любой треугольник можно вписать только одну
окружность, которая находится внутри треугольника.
Центр вписанной окружности равноудален от всех
сторон треугольника. Точка, где окружность пересекается
со стороной треугольника, называется точкой касания.
Все отрезки, которые проведены от точки касания к центру
вписанной окружности имеют одинаковую длину.
Чтобы найти радиус окружности вписанной в треугольник
надо площадь разделить на полупериметр.
Диаметр вписанной окружности в треугольник численно
равен двум радиусам вписанной окружности. Радиус
вписанной окружности можно найти по разным
формулам, все зависит от того, какой треугольник.
Всего различают четыре вида треугольников:
- Разносторонний / любой
- Правильный / равносторонний
- Равнобедренный / равнобочный
- Прямоугольный / прямой
Радиус вписанной окружности в любой треугольник
- Радиус вписанной окружности в любой треугольник через площадь и полупериметр
S — площадь; p — полупериметр;
Радиус вписанной окружности в любой треугольник через все стороны и полупериметр
a, b, c — стороны; p — полупериметр;
Радиус вписанной окружности в любой треугольник через основание, высоту и полупериметр
a — основание, сторона на которую падает высота; h — высота; p — полупериметр;
Радиус вписанной окружности в любой треугольник через диаметр вписанной окружности
D — диаметр вписанной окружности;
Радиус вписанной окружности в правильный треугольник
- Радиус вписанной окружности в правильный треугольник через сторону
a — сторона;
Радиус вписанной окружности в правильный треугольник через радиус описанной окружности
R — радиус описанной окружности;
Радиус вписанной окружности в правильный треугольник через диаметр вписанной окружности
D — диаметр вписанной окружности;
Радиус вписанной окружности в равнобедренный треугольник
- Радиус вписанной окружности в равнобедренный треугольник через боковые стороны и основание
a — боковая сторона; b — основание;
Радиус вписанной окружности в равнобедренный треугольник через высоту и основание
b — основание; h — высота;
Радиус вписанной окружности в равнобедренный треугольник через диаметр вписанной окружности
D — диаметр вписанной окружности;
Радиус вписанной окружности в прямоугольный треугольник
- Радиус вписанной окружности в прямоугольный треугольник через два катета и гипотенузу
a, b — катеты; с — гипотенуза.
Радиус вписанной окружности в прямоугольный треугольник через гипотенузу и два катета
c — гипотенуза; a, b — катеты;
Радиус вписанной окружности в прямоугольный треугольник через диаметр вписанной окружности
D — диаметр вписанной окружности;
Вписанная окружность в треугольник — это окружность,
которая вписана в треугольник и касается всех его сторон.
Радиус вписанной окружности в треугольник — это отрезок,
проведенный от центра вписанной окружности до любой стороны.
Длина радиуса вписанной окружности, диаметра
вписанной окружности а также других величин
измеряется в мм, см, м, км и так далее.
В любом треугольнике все радиусы и диаметры
равны, имеют одинаковую длину.
Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

Найдите радиус окружности вписанной в треугольник 60
Центр O окружности радиуса 4 принадлежит биссектрисе угла величиной 60°. Найдите радиус окружности, вписанной в данный угол и касающейся данной окружности, если известно, что расстояние от точки O до вершины угла равно 10.
Пусть Q — центр искомой окружности радиуса x, B — точка касания одной из сторон данного угла с вершиной A. Центр окружности, вписанной в угол, лежит на биссектрисе угла, поэтому ∠BAQ = 30°. Из прямоугольного треугольника BAQ находим, что AQ = 2QB = 2x. Рассмотрим случай внешнего касания окружностей. Если точка Q лежит между A и O (см. рис.), то AO = AQ + QO, или 10 = 2x + (x + 4), откуда находим, что x = 2.
Если точка O лежит между A и Q (см. рис.), то AQ = AO + OQ, или 2x = 10 + (4 + x), откуда x = 14.
Рассмотрим случай внутреннего касания окружностей. Если точка Q лежит между A и O (см. рис.), то AO = AQ + QO, или 10 = 2x + (x − 4), откуда находим, что
Если точка O лежит между A и Q (см. рис.), то AQ = AO + OQ, или 2x = 10 + (x − 4), откуда x = 6.
Ответ: 2; 14; 6.
Аналоги к заданию № 484626: 507383 511306 511424 Все
Видео:Задание 16 ОГЭ по математике. Окружность вписана в равносторонний треугольник.Скачать

Нахождение радиуса вписанной в треугольник окружности
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, вписанной в произвольный (любой), прямоугольный, равнобедренный или равносторонний треугольник. Также разберем примеры решения задач для закрепления представленного теоретического материала.
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Формулы вычисления радиуса вписанной окружности
Произвольный треугольник
Радиус окружности, вписанной в любой треугольник, равняется удвоенной площади треугольника, деленной на его периметр.
где a, b, c – стороны треугольника, S – его площадь.
Прямоугольный треугольник
Радиус окружности, вписанной в прямоугольный треугольник, равняется дроби, в числителе которого сумма катетов минус гипотенуза, в знаменателе – число 2.
где a и b – катеты, c – гипотенуза треугольника.
Равнобедренный треугольник
Радиус вписанной в равнобедренный треугольник окружности вычисляется по формуле ниже:
где a – боковые стороны, b – основание треугольника.
Равносторонний треугольник
Радиус вписанной в правильный (равносторонний) треугольник окружности рассчитывается следующим образом:
где a – сторона треугольника.
Видео:Сможешь найти радиус окружности? Окружность, вписанная в прямоугольный треугольникСкачать

Примеры задач
Задание 1
Дан треугольник со сторонами 5, 7 и 10 см. Вычислите радиус вписанной в него окружности.
Решение
Сперва вычислим площадь треугольника. Для этого применим формулу Герона:
Остается только применить соответствующую формулу для вычисления радиуса круга:
Задание 2
Боковые стороны равнобедренного треугольника равны 16 см, а основание 7 см. Найдите радиус вписанной в фигуру окружности.
Решение
Воспользуемся подходящей формулой, подставив в нее известные значения:
📺 Видео
Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Задача 6 №27892 ЕГЭ по математике. Урок 126Скачать

Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать

ЕГЭ профиль #3 / Радиус описанной окружности / Равносторонний треугольник / решу егэСкачать

Задание 16 ОГЭ по математике. Две окружности одна описана около квадрата, другая вписана в него.Скачать

Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

ЕГЭ 6 номер. Нахождение стороны правильного треугольника по радиусу вписанной окружности.Скачать

2047 радиус окружности описанной около правильного треугольника равна 36 корней из 3Скачать

Вписанная и описанная окружность - от bezbotvyСкачать