Видео:Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать
Ваш ответ
Видео:Задача 6 №27951 ЕГЭ по математике. Урок 149Скачать
решение вопроса
Видео:ЕГЭ Математика Задание 6#27952Скачать
Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 607,036
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Задача 6 №27913 ЕГЭ по математике. Урок 131Скачать
Прямоугольник и прямоугольный треугольник: радиус вписанной и описанной окружности. Задание В6
При решении задач на нахождение радиуса вписанной или описанной окружности нужно вспомнить такие факты:
1. Центр окружности, описанной около прямоугольного треугольника лежит в середине гипотенузы. Соответственно, радиус окружности, описанной около прямоугольного треугольника равен половине гипотенузы.
2. Центр окружности, описанной около прямоугольника или квадрата, лежит в точке пересечения диагоналей.
3. Радиус окружности, вписанной в квадрат, равен половине стороны квадрата.
4. Центр окружности, вписанной в равносторонний треугольник, а также центр окружности, описанной около равностороннего треугольника лежит в точке пересечения медиан ( высот и биссектрис).
И, так как точка пересечения медиан любого треугольника делит их в отношении 2:1, считая от вершины,
- радиус окружности, вписанной в равносторонний треугольник равен
медианы (высоты, биссектрисы) равностороннего треугольника, и - радиус окружности, описанной около равностороннего треугольника равен медианы (высоты, биссектрисы) равностороннего треугольника
медианы (высоты, биссектрисы) равностороннего треугольника, и
медианы (высоты, биссектрисы) равностороннего треугольника5. Радиус окружности, вписанной в прямоугольный треугольник, удобно находить, дважды выразив площадь прямоугольного треугольника:
, где 
и 
— катеты прямоугольного треугольника, 
— полупериметр прямоугольного треугольника, 
— радиус вписанной окружности.
Рассмотрим примеры решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике:
1 . Задание B7 (№ 27947)
Найдите радиус окружности, описанной около прямоугольника ABCD, если стороны квадратных клеток равны 1. 
Центр окружности, описанной около прямоугольника лежит в точке пересечения диагоналей:
Очевидно, что точка О делит отрезок BD пополам (диагонали прямоугольника делятся точкой пересечения пополам). Длина отрезка BD равна 5( считаем клетки), следовательно, радиус описанной окружности равен 2,5.
2 . Задание B7 (№ 27948)
Найдите радиус окружности, вписанной в квадрат ABCD, считая стороны квадратных клеток равными
. 
ОК- радиус окружности, вписанной в квадрат ABCD:
ОК — диагональ квадрата со стороной 
, следовательно,
3 . Задание B7 (№ 27949)
Найдите радиус R окружности, описанной около треугольника ABC, если стороны квадратных клеток равны 1. В ответе укажите 
.
Центр окружности, описанной около прямоугольного треугольника лежит в середине гипотенузы:
Найдем длину отрезка СО, равного радиусу описанной окружности, из треугольника СОК: 
В ответе требуется указать 
4 . Задание B7 (№ 27950)
Найдите радиус окружности, описанной около правильного треугольника ABC, считая стороны квадратных клеток равными 1.
Центр О описанной окружности лежит в точке пересечения медиан (высот и биссектрис) треугольника ABC.
Высота (она же медиана) ВК=3, следовательно, 
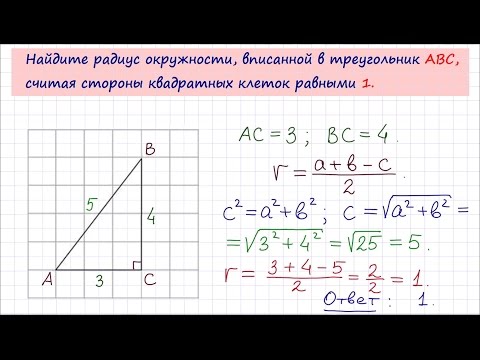
5 . Задание B7 (№ 27951)
Найдите радиус окружности, вписанной в треугольник ABC, считая стороны квадратных клеток равными 1.
Считаем клеточки: AC=3, BC=4. По теореме Пифагора 
И.В. Фельдман, репетитор по математике.
Видео:Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать
Найдите радиус окружности если стороны квадратных клеток равны 1
Прототип задания B8 (№ 27951)
Найдите радиус окружности, вписанной в треугольник ABC, считая стороны квадратных клеток равными 1.
Прототип задания B8 (№ 27934)
Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.
По условию AC = BC = 5, AB = 6. Проведем высоту CH.
Прототип задания B8 (№ 27933)
В треугольнике ABC AC = 4, BC = 3, угол C равен 
. Найдите радиус вписанной окружности.
Прототип задания B8 (№ 27932)
Катеты равнобедренного прямоугольного треугольника равны 
. Найдите радиус окружности, вписанной в этот треугольник.
Прототип задания B8 (№ 27930)
Угол между двумя соседними сторонами правильного многоугольника, вписанного в окружность, равен 
. Найдите число вершин многоугольника.
Градусная величина правильного многоугольника вычисляется по формуле:
Здесь n — число вершин правильного многоугольника.
📹 Видео
Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать
Найдите высоту треугольника АВС, опущенную на сторону BC, если стороны квадратных клеток равныСкачать
ЕГЭ Математика . Задание 3 #9Скачать
Задание 3 ЕГЭ по математике. Урок 11Скачать
Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать
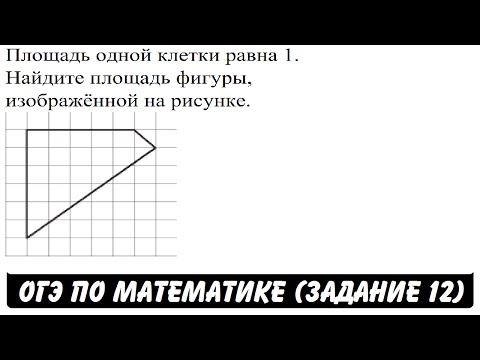
Площадь одной клетки равна 1. Найдите площадь фигуры ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать
ЕГЭ Математика . Задание 3 #8Скачать
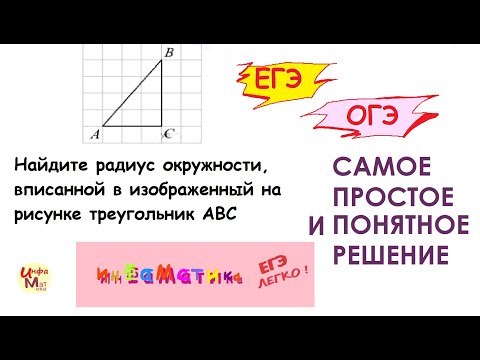
Найдите радиус окружности, вписанной в изображенный на рисунке треугольник ABCСкачать
Самый простой способ нахождения площадиСкачать
Задание 16 ОГЭ по математике. Окружность описана около квадратаСкачать
Задание В6.mp4Скачать
Задание В6Скачать
Задание В6 .mp4Скачать
ЕГЭ профиль #3 / Многоугольники: вычисление длин и углов / Биссектриса, медиана, высота / решу егэСкачать
Задача 6 №27900 ЕГЭ по математике. Урок 128Скачать
