Треугольник с выпуклыми сторонами (8 видео)

Трегольник Рёло

Колесо — это предмет, как правило, круглой формы, служащий для передачи или регулирования движения.

Содержание

Кривые постоянной ширины
Как построить треугольник Рёло
Треуольник Рело: применение
Интересный факт о кривых постоянной ширины
Круглый треугольник Рело ⁠
РЕЛО Франц 1829—1905
«Треугольник рело»
Применение в автомобильных двигателях
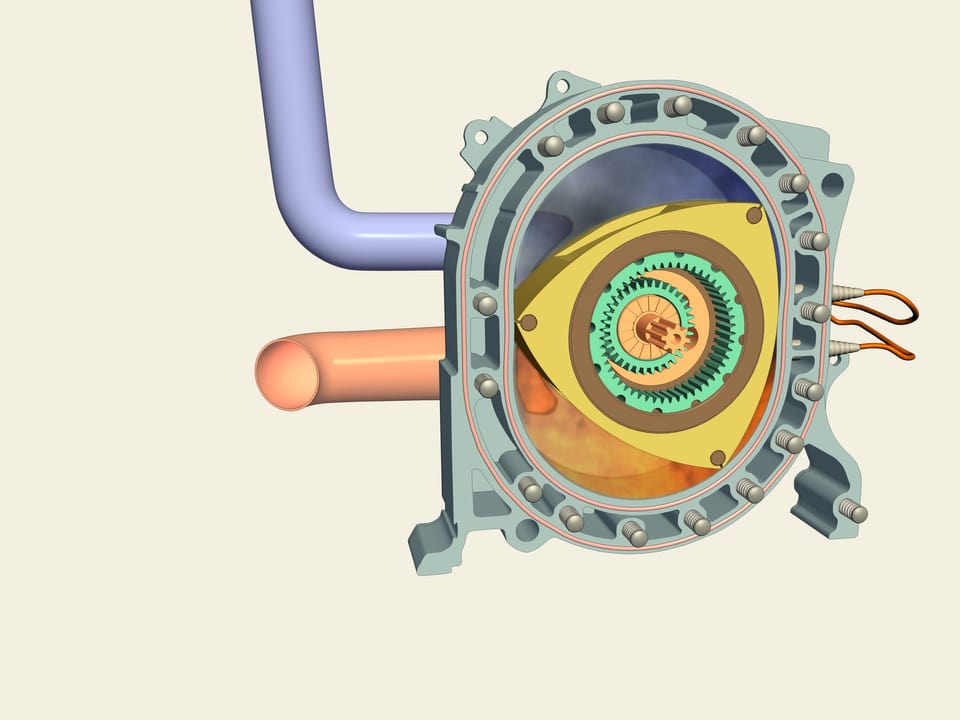
Фактически каждая из трёх боковых поверхностей ротора действует как поршень. При всех достоинствах РПД — компактности, приемистости, отсутствии кривошипно-шатунного и газораспределительного механизмов, а так же значительно меньших габаритов и массе при одинаковой с поршневыми двигателями внутреннего сгорания мощности, он имеет и ряд серьезных недостатков: часто выходящие из строя уплотнительные элементы, плохая приспосабливаемость к изменениям внешней нагрузки, повышенный расход топлива и неудовлетворительные показатели по выбросам в отработавших газах. Тем не менне в серийном производстве находятся автомобили Mazda RX-8.
Треугольник Рёло в искусстве, архитектуре и литературе
Заключение
2. Треугольник Рёло// Материал из Википедии — свободной энциклопедии
📸 Видео

Кривые постоянной ширины

Использование колес для перемещения грузов по плоским поверхностям возможно благодаря тому, что все радиусы окружности имеют одинаковую длину. Так как окружность — это геометрическое место точек, равноудаленных от центра. Поэтому если ось вращения колеса проходит через его центр, то она не поднимается и не опускается, а только перемещается вперед или назад, при этом высота над поверхностью остается неизменной. Существует и другой способ перемещения грузов, в котором вместо колес используются валы. Все мы не раз видели на картинках, как огромный каменный блок стоит на нескольких валах и его толкают или тянут веревками

Это возможно благодаря еще одному свойству окружностей, которое не имеет ничего общего с тем, о чем мы только что говорили. Колеса могут иметь только круглую форму, в то время как форма валов может быть различной.

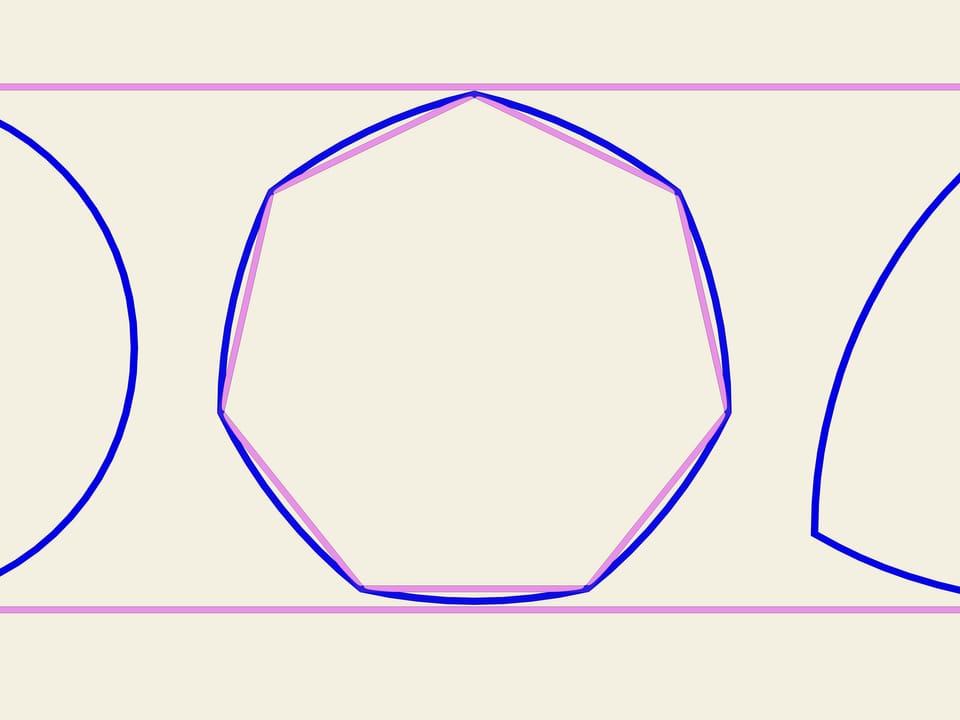
Свойство, благодаря которому действуют валы, связано не с расположением центра окружности, а с шириной круга, которая постоянна в любом направлении. Рассмотрим в качестве примера эллипс. Ширина эллипса вдоль большой оси очевидно больше, чем вдоль малой оси. Нетрудно представить, что произойдет, если мы подложим под камень валы в форме эллипса.

Камень при движении будет перемещаться вверх-вниз, пока не упадет на землю. Любопытно, но окружность не единственная кривая постоянной ширины. Существует бесконечное множество подобных прямых, которые подчас имеют весьма причудливую форму

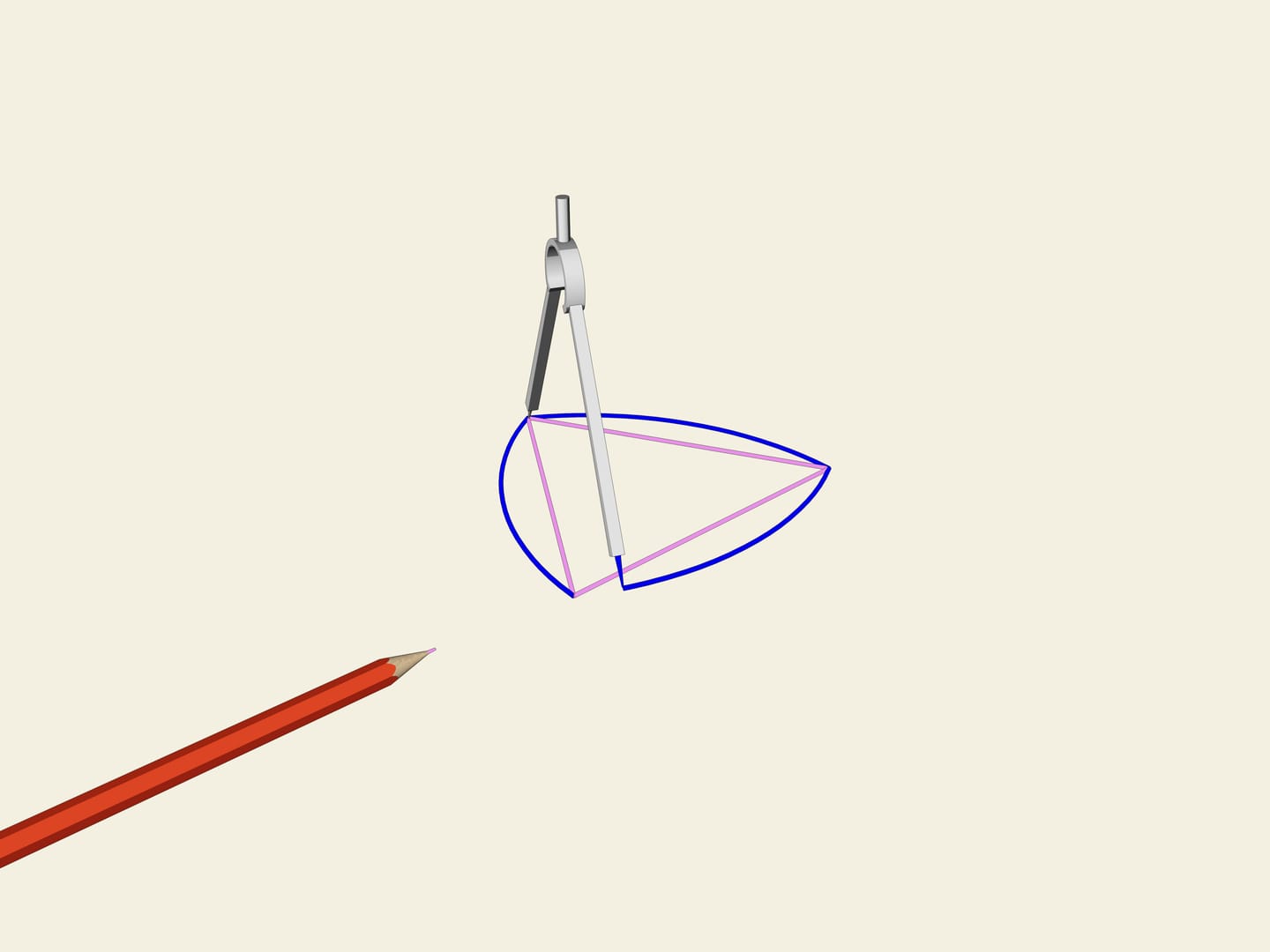
Как построить треугольник Рёло

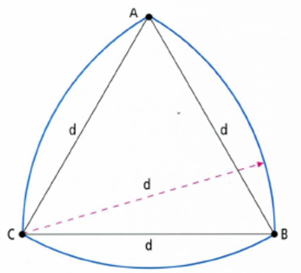
Пусть дан равносторонний треугольник с вершинами А, В и С. Возьмем циркуль и проведем дугу окружности с центром в точке А через вершины В и С. Затем проведем дугу окружности с центром в точке В. Дуга пройдет через вершины С и А. После этого выполним аналогичные действия для вершины С.

Полученная фигура называется треугольником РЁЛО и является кривой постоянной ширины. Если использовать вал подобной формы, он ничем не будет отличаться от круглого вала. При вращении треугольник Рёло всегда соприкасается с поверхностью земли и блока, поскольку он всегда вращается вокруг одной из вершин, а расстояние от неё до дуги окружности является постоянной величиной

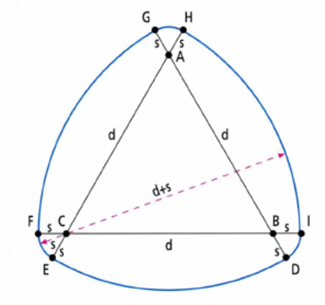
Вершинами треугольника Рёло могут быть скругленными, и при этом он по-прежнему будет обладать постоянной шириной. Чтобы построить такой треугольник, достаточно продлить его стороны на произвольное расстояние, затем, зафиксировав центр окружности в одной из вершин, соединить концы продленных сторон дугами, как показано на рисунке:

Все вышесказанное можно обобщить и для трех измерений, то есть можно построить геометрические тела постоянной ширины, подобные сфере. Простейшее из них можно получить вращением треугольника Рёло вокруг одной из его осей симметрии. Еще одно подобное тело можно получить, проведя аналогичные построения, но в пространстве: за основу берется пирамида, а не треугольник, и поверх ее граней строятся части сферы. Полученное тело будет вращаться в пространстве аналогично треугольнику на плоскости

Треуольник Рело: применение

Классические кинопроекторы всегда издают характерный стрекочущий звук. Он возникает из-за использования треугольников Рёло в механизме проектора. При показе фильма на экране на очень короткий промежуток времени (1/24 секунды) показывается кадр, после чего кинопленку необходимо провернуть, чтобы показать на экране следующий кадр. В этот момент затвор должен быть закрыт, чтобы на экране не было расплывчатого изображения. Получается, что движение ленты должно чередоваться с остановками. Это достигается путем равномерного вращения треугольника Рёло вокруг одной из его вершин. Треугольник Рёло находится внутри прямоугольной рамки, которая поднимается и опускается. Рамка остается неподвижной половину периода вращения треугольника, после чего перемещается в новое положение, где остается неподвижной такое же время. Затем весь цикл повторяется

Другое важное применение кривых постоянной ширины основано на возможности построения выпуклой кривой, внутри которой треугольник Рёло может перемещаться так чтобы все его вершины постоянно соприкасались с этой кривой. Благодаря этому свойству немецкий инженер Феликс Ванкель в 1924 году спроектировал роторный двигатель, в котором поршни были заменены ротором в форме треугольника Рёло. Ротор вращается внутри кривой необходимых размеров, точно подобранных для корректной работы четырехтактного двигателя внутреннего сгорания. Первый прототип под названием DKM был изготовлен в 1957 году, о результат оставлял желать лучшего из-за сильной вибрации на малой скорости, большого расхода масла и невысокого момента. Сейчас применяется уже третье поколение подобных двигателей (Rx-7), их объём доведен до 1 308 кубических сантиметров, мощность атмосферного двигателя при 8 200 оборотах в минуту составляет 227 лошадиных сил. Классический поршневой двигатель той же мощности будет иметь шесть цилиндров и объём более трех литров

Как сверлить квадратные отверстия?

Можно ли просверлить квадратное отверстие? Здравый смысл подсказывает, что нет, но на самом деле это возможно. В этом нам помогут кривые постоянной ширины. Представим себе окружность, вписанную в квадрат. При вращении она всегда касается всех его сторон, причем точки касания всегда располагаются на серединах сторон. При вращении треугольник Рёло нужных размеров также может постоянно касаться всех сторон квадрата, но в разных точках, так как его ширина постоянна. Каждая вершина треугольника опишет квадрат со скругленными углами. В начале ХХ века это свойство натолкнуло британского инженера Гарри Джеймса Уоттса на мысль о возможности сверления квадратных отверстий. Добавим, что этот же принцип позволяет сверлить отверстия форме любых многоугольников с четным числом сторон. В сверлильном станке Уоттса центр вращения треугольника Рёло не фиксирован. Описываемая замкнутая кривая выглядит как идеальный квадрат, но в действительности представляет собой более сложную кривую, образованную четырьмя дугами эллипса. Скругленные углы квадратного отверстия также являются дугами эллипса.

Интересный факт о кривых постоянной ширины

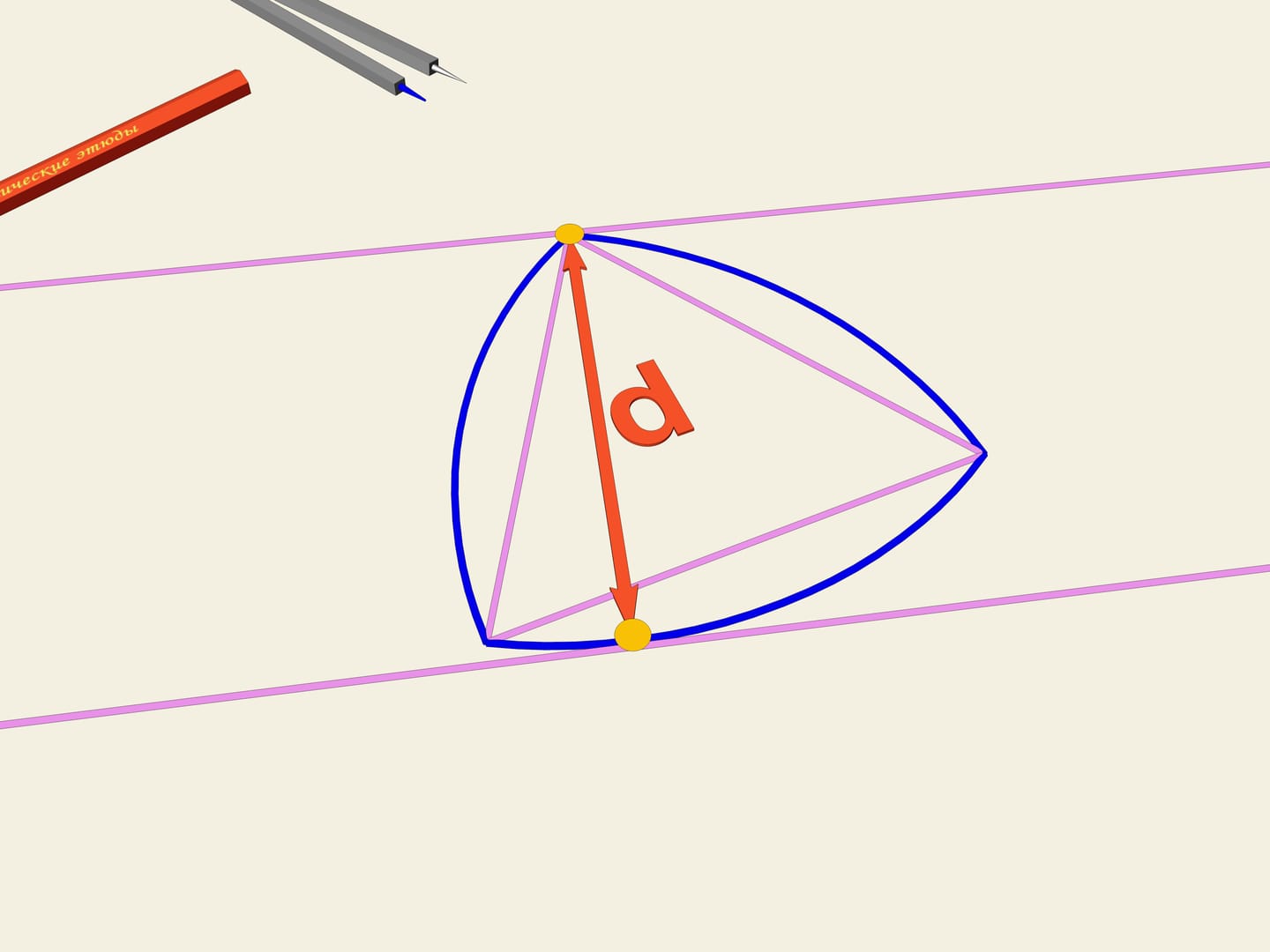
Кривые постоянной ширины обладают некоторыми примечательными свойствами. Рассмотрим, например, простой треугольник Рёло и вычислим его периметр. Он состоит из трёх равных круговых секторов с углом 60° и радиусом d, равным длине стороны треугольника. Так как 60° – это одна шестая от 360, длине дуги L для каждого сектора равна шестой части длины всей окружности C.

Иными словами:
L = 1/6 х C = 1/6 x 2пd = 1/3пd.
Общий периметр Р получается сложением длин дуг трех круговых секторов. Имеем:
Р=3 х (1/3 па) = пd
Это в точности совпадает с периметром окружности диаметра d, которая также является кривой постоянной ширины, равной d. Самым примечательным является тот факт, что это не случайное совпадение, а общий результат, одинаковый для всех подобных кривых. Можно показать, что все кривые равной постоянной ширины вне зависимости от формы имеют равный периметр.

Площадь этих кривых, даже если их ширина совпадает, изменяется в зависимости от формы фигуры. Однако треугольник Рёло занимает особое место. Его площадь, примерно равная 0,705d^2, что является минимально возможной.

Франц Рёло

Хотя кривые постоянной ширины были известны с древних времен, треугольники Рёло впервые изучил инженер и математик Франц Рёло (1829-1905), преподаватель Берлинской королевской технической академии. Он выполнил исследование всех механизмов, имевших большое значение в различные моменты истории. За огромный вклад в развитие математики, в 1912 году в Дании ему был установлен памятник.

Подготовка к ОГЭ по математике 2020 — задания 1 — 5 с подробными решениями.

Видео:Соотношения между сторонами и углами треугольника. 7 класс.Скачать

Круглый треугольник Рело ⁠

Проектор восьмимиллиметровой киноплёнки «Луч-2». Именно он был в каждом доме, где сами снимали и смотрели киноэтюды.

В этом мультфильме рассказывается, как геометрическое понятие, часто изучаемое на математических кружках, находит применение в нашей повседневной жизни.

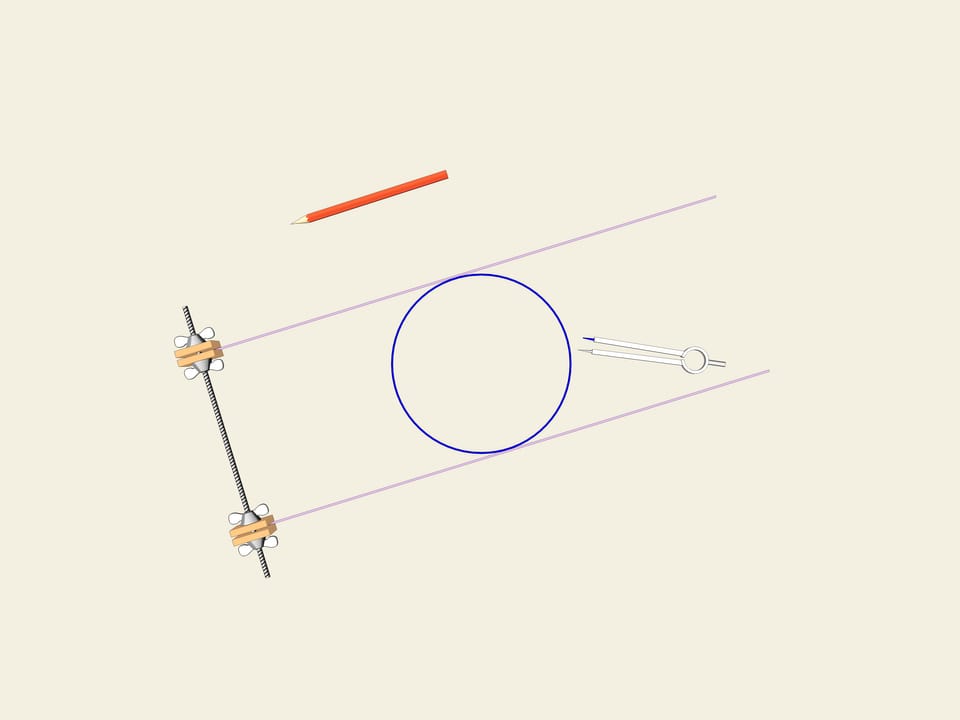
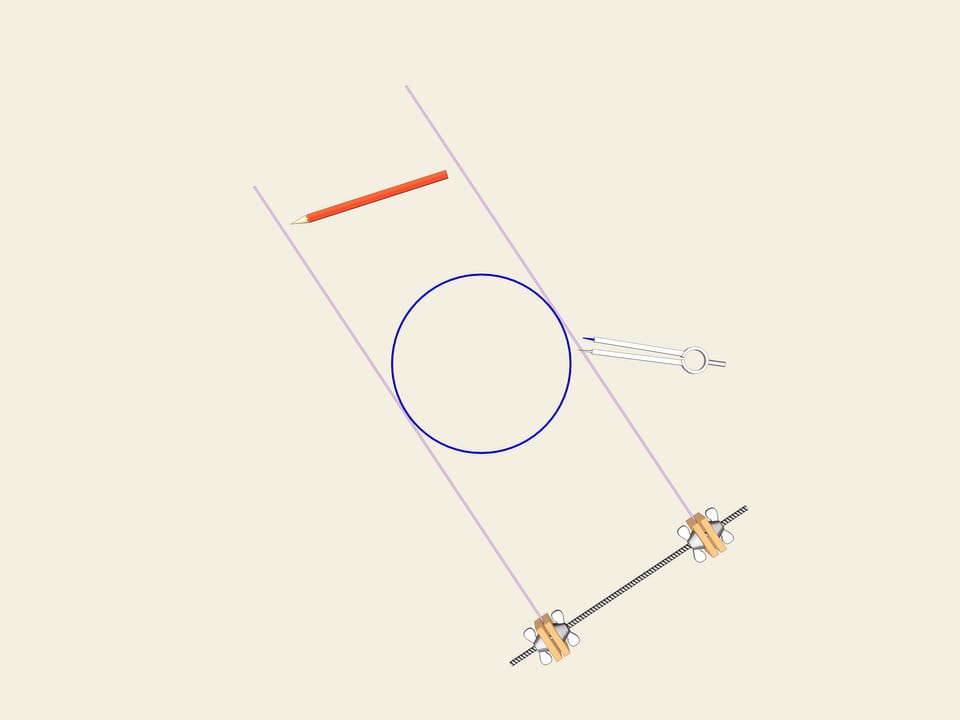
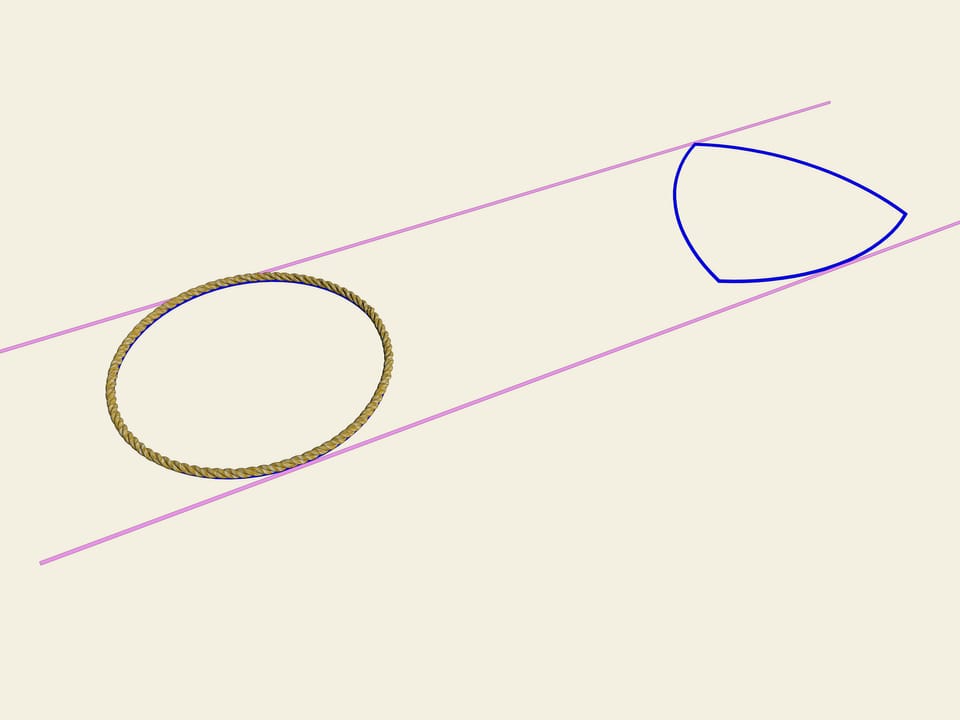
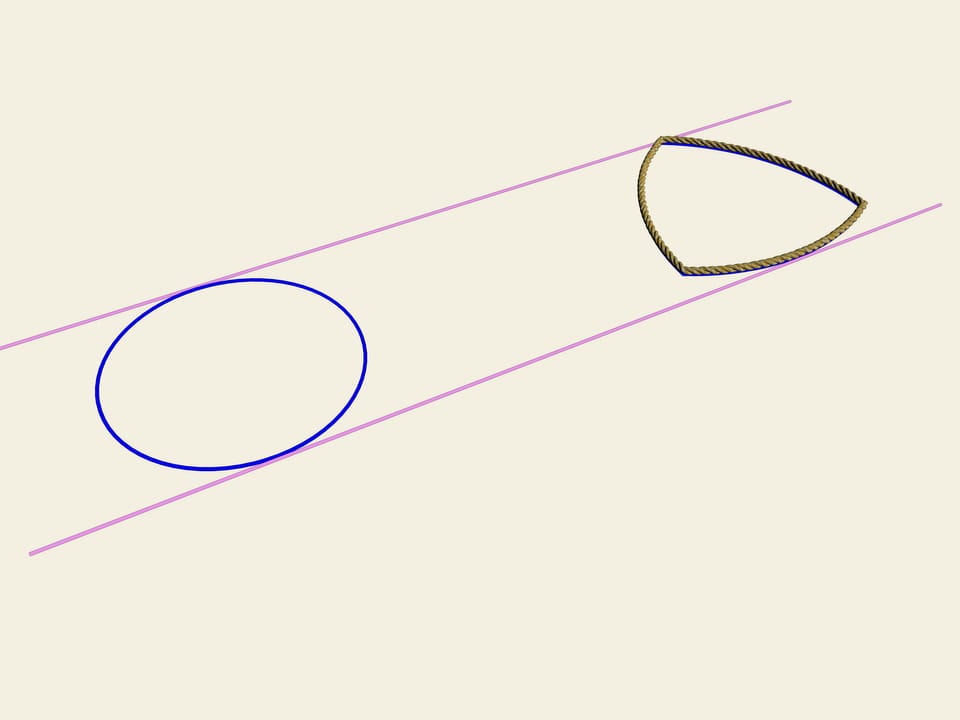
Колесо… Окружность. Одним из свойств окружности является ее постоянная ширина. Проведём две параллельные касательные и зафиксируем расстояние между ними. Начнём вращать. Кривая (в нашем случае окружность) постоянно касается обеих прямых. Это и есть определение того, что замкнутая кривая имеет постоянную ширину.

Бывают ли кривые, отличные от окружности и имеющие постоянную ширину?

РЕЛО Франц 1829—1905

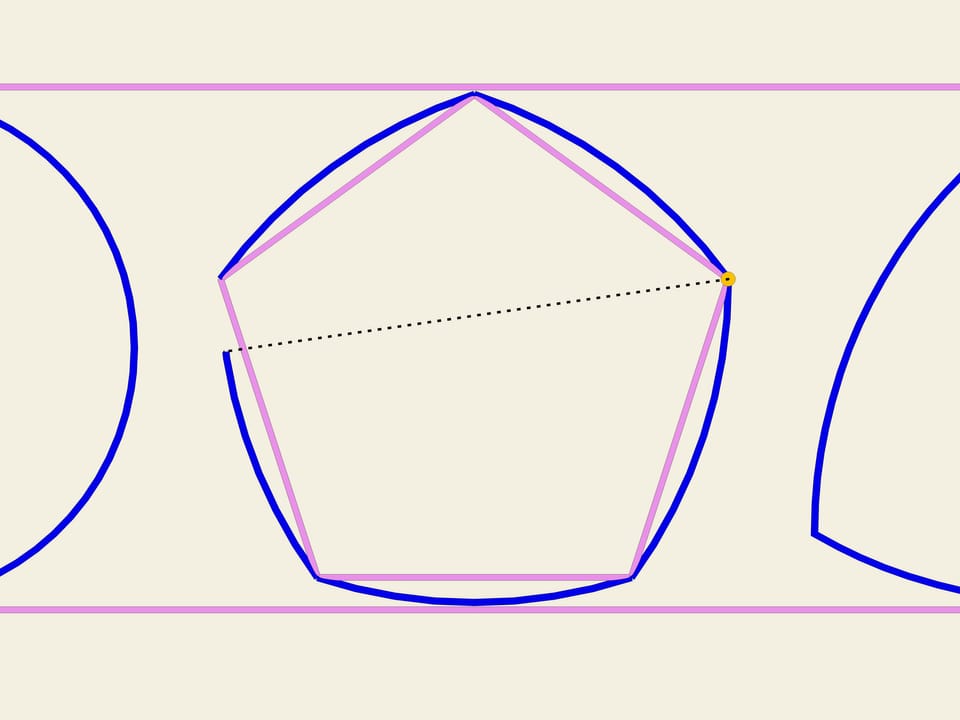
Рассмотрим правильный треугольник (с равными сторонами). На каждой стороне построим дугу окружности, радиусом, равным длине стороны. Эта кривая и носит имя «треугольник Рело». Оказывается, она тоже является кривой постоянной ширины. Как и в случае окружности проведём две касательные, зафиксируем расстояние между ними и начнём их вращать. Треугольник Рело постоянно касается обеих прямых. Действительно, одна точка касания всегда расположена в одном из «углов» треугольника Рело, а другая — на противоположной дуге окружности. Значит, ширина всегда равна радиусу окружностей, т. е. длине стороны изначального правильного треугольника.

В житейском смысле постоянная ширина кривой означает, что если сделать катки с таким профилем, то книжка будет катиться по ним, не шелохнувшись.

Однако колесо с таким профилем сделать нельзя, так как её центр описывает сложную линию при качении фигуры по прямой.

Бывают ли какие-то ещё кривые постоянной ширины? Оказывается, их бесконечно много.

На любом правильном n-угольнике с нечётным числом вершин можно построить кривую постоянной ширины по той же схеме, что был построен треугольник Рело. Из каждой вершины, как из центра, проводим дугу окружности на противоположной вершине стороне. В Англии монета в 20 пенсов имеет форму кривой постоянной ширины, построенной на семиугольнике.

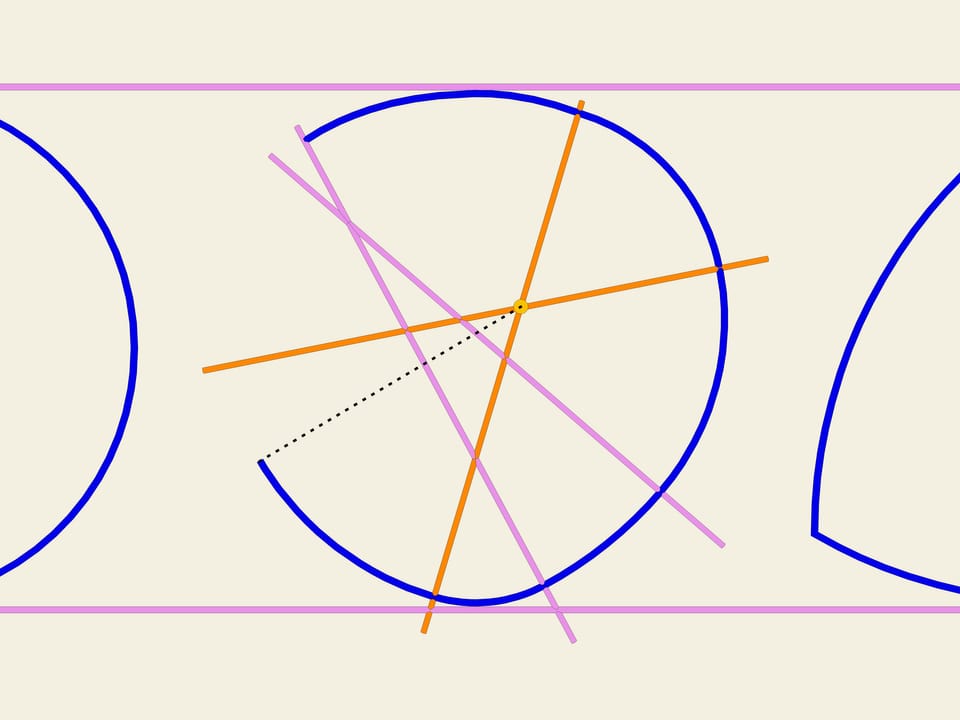
Рассмотренные кривые не исчерпывают весь класс кривых постоянной ширины. Оказывается, среди них бывают и несимметричные кривые. Рассмотрим произвольный набор пересекающихся прямых. Рассмотрим один из секторов. Проведём дугу окружности произвольного радиуса с центром в точке пересечения прямых, определяющих этот сектор. Возьмём соседний сектор, и с центром в точке пересечения прямых, определяющих его, проведём окружность. Радиус подбирается такой, чтобы уже нарисованный кусок кривой непрерывно продолжался. Будем так делать дальше. Оказывается, при таком построении кривая замкнётся и будет иметь постоянную ширину. Докажите это!

Все кривые данной постоянной ширины имеют одинаковый периметр. Окружность и треугольник Рело выделяются из всего набора кривых данной ширины своими экстремальными свойствами. Окружность ограничивает максимальную площадь, а треугольник Рело — минимальную в классе кривых данной ширины.

Треугольник Рело часто изучают на математических кружках. Оказывается, что эта геометрическая фигура имеет интересные приложения в механике.

Смотрите, это «Мазда RX-7». В отличие от большинства серийных машин в ней (а также в модели RX-8) стоит роторный двигатель Ванкеля. Как же он устроен внутри? В качестве ротора используется именно треугольник Рело! Между ним и стенками образуются три камеры, каждая из которых по очереди является камерой сгорания. Вот вспрыснулась синяя бензиновая смесь, далее из-за движения ротора она сжимается, поджигается и крутит ротор. Роторный двигатель лишён некоторых недостатков поршневого аналога — здесь вращение передается сразу на ось и не нужно использовать коленвал.

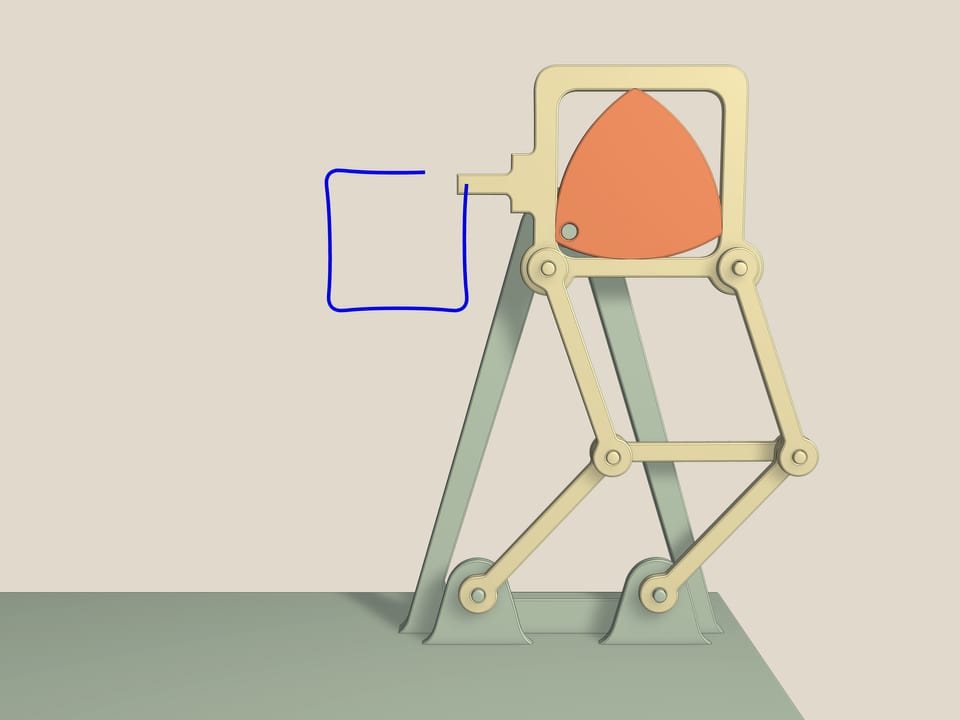
А это — грейферный механизм. Он использовался в кинопроекторах. Двигатели дают равномерное вращение оси, а чтобы на экране было чёткое изображение, плёнку мимо объектива надо протянуть на один кадр, дать ей постоять, потом опять резко протянуть, и так 18 раз в секунду. Именно эту задачу решает грейферный механизм. Он основан на треугольнике Рело, вписанном в квадрат, и двойном параллелограмме, который не даёт квадрату наклоняться в стороны. Действительно, так как длины противоположных сторон равны, то среднее звено при всех движениях остаётся параллельным основанию, а сторона квадрата — всегда параллельной среднему звену. Чем ближе ось крепления к вершине треугольника Рело, тем более близкую к квадрату фигуру описывает зубчик грейфера.

Вот такие интересные применения, казалось бы, чисто математической задачи используют люди.

Видео:Сумма внутренних углов многоугольника. Выпуклые и невыпуклые многоугольники. 8 класс.Скачать

«Треугольник рело»

Международный Фестиваль «Звезды Нового Века» — 2013

Точные науки (от 14 до 17 лет)

Шорин Алихан 14 лет,

Мачнев Александр 14 лет

КГУ «Комплекс школа-детский

Глава 1. Основные геометрические характеристики и свойства тре-

1.1.Построение треугольника Рело циркулем _____________________3

1.2.Основные геометрические характеристики и свойства треугольни-

ка Рело ______________________________________________________4

Глава 2. История изобретения и применение треугольника Рело

2.2.История изобретения треугольника Рело ______________________7

2.3.Применение треугольника Рело ______________________________7

2.4.Изобретение велосипеда с треугольными колесами ____________10

Заключение ___________________________________________________ 10

Список используемых источников ______________________________11

Приложение 1. Использование треугольника Рело в архитектуре 12

«Изобретением велосипеда» называют бессмысленное повторение и переоткрытие давно пройденного и известного, и совершенно напрасно. Современные инженеры, можно сказать, постоянно изобретают велосипед, внося все новые усовершенствования в его конструкцию и отдельные детали. Однажды в интернете мы прочитали об одном удивительном изобретении китайского пенсионера – велосипеде с треугольными колесами (Рис. 1). Нас заинтересовало не только само по себе данное изобретение, но и необычная геометрическая фигура – круглый треугольник. Мы узнали, что он называется треугольником Рело и посвятили свою работу изучению его свойств и областей применения. А заодно поставили задачу выяснить, как геометрия позволяет этому чуду катиться и иметь удивительно плавный ход.

Рисунок 1 . Велосипед с треугольными колесами

Цель работы — изучить основные свойства треугольника Рело, историю его изобретения, рассмотреть области применения, выявить задачи, связанные с треугольником Рело.

Для этого поставлены следующие задачи:

Ø Познакомиться с историей изобретения;

Ø Рассмотреть и изучить свойства треугольника Рело;

Ø Выяснить области применения треугольника Рело.

Ø Найти объяснение плавности хода велосипеда с «треугольными колесами»

Гипотеза: Треугольнику Рело присущи свойства обеих геометрических фигур, используемых в его построении, кроме того он обладает собственными свойствами, которые используются в технике.

Теоретическая значимость исследования состоит в описании, всестороннем анализе, сопоставлении свойств геометрических фигур, опережающем изучении формул площадей фигур, обощении и систематизации материала по теме проекта.

Практическая значимость состоит в том, что результаты работы могут найти применение в курсах по выбору, программах факультативов, основой для разработки внеклассных занятий по математике и интегрированных уроков математики и физики. Работа над темой существенно расширит представления о «круглом» треугольнике, семействе фигур постоянной ширины.

Определение: Треуго́льник Рёло́ представляет собой область пересечения трёх равных кругов с центрами в вершинах правильного треугольника и радиусами, равными его стороне. Негладкая замкнутая кривая, ограничивающая эту фигуру, также называется треугольником Рёло [ 1 ].

Построение треугольника Рело циркулем:

Рисунок 2. Построение треугольника Рело

Треугольник Рёло можно построить с помощью одного только циркуля, не прибегая к линейке. Это построение сводится к последовательному проведению трёх равных окружностей. Центр первой выбирается произвольно, центром второй может быть любая точка первой окружности, а центром третьей — любая из двух точек пересечения первых двух окружностей.

Основные геометрические характеристики

1. Треугольник Рёло – также как и круг — кривая постоянной ширины.

Данные утверждения проверены опытным путем, вращением трех геометрических фигур между двумя опорными прямыми:

Рисунок 3. Доказательство постоянства ширины

2. Периметр треугольника Рело и совпадает с периметром круга. Формула доказана опытным путем рис. 2, в математике носит название теоремы Барбье.

Рисунок 4. Определение периметра круга и треугольника Рело

3. Площадь Также как и обычный треугольник, круг, треугольник Рёло является плоской выпуклой геометрической фигурой, которая имеет определенную площадь, которая может быть вычислена по формуле . Формула выведена аналитическим методом, используя соотношение: S=Scегм , и методом разрезания и сложения площадей (рис. 5). S=Scегм

cегм=Sсект — S=

SРело=— =(.

Следовательно, площадь треугольника Рело равна

SРело=(

Площадь треугольника Рело меньше площади круга.

Рисунок 5. Определение площади треугольника Рело

Среди всех фигур постоянной ширины у треугольника Рёло наименьшая площадь. Это утверждение носит название теоремы Бляшке — Лебега (по фамилиям немецкого геометра Вильгельма Бляшке, опубликовавшего теорему в 1915 году, и французского математика Анри Лебега, который сформулировал её в 1914 году SРело=(

Фигура, обладающая противоположным экстремальным свойством — круг. Среди всех фигур данной постоянной ширины его площадь

Sкруга= максимальна

Площадь соответствующего треугольника Рёло меньше на ≈10,27 %. В этих пределах лежат площади всех остальных фигур данной постоянной ширины.

Треугольник Рёло обладает осевой и центральной симметрией

5. Замечательные точки треугольника

Центры вписанной, описанной окружностей, ортоцентр и центр тяжести совпадают. Сумма радиусов вписанной и описанной окружностей равна ширине треугольника Рело. )a (рис. 4 )

Рисунок 6. Замечательные точки

6. Треугольник Рело можно вписать в квадрат, он может вращаться квадрате со стороной а, всё время касаясь каждой из сторон. В работе

рассмотрена траектория движения вершины треугольника при вращении в квадрате и при движении треугольника по прямой. Показано, что так же как и у круга, траектория движения по прямой – циклоида.

Каждая вершина треугольника при его вращении в квадрате «проходит» почти весь периметр квадрата, отклоняясь от этой траектории лишь в углах — там вершина описывает дугу эллипса. Центр треугольника Рёло при вращении движется по траектории, составленной из четырёх одинаковых дуг эллипсов. Центры этих эллипсов расположены в вершинах квадрата, а оси повёрнуты на угол в 45° относительно сторон квадрата и равны

а*(1)

Траектория центра треугольника Рёло при вращении в квадрате. Выделены точки сопряжения четырёх дуг эллипсов. Для сравнения показана окружность (синим цветом), проходящая через эти же четыре точки

Рисунок 7 Траектории движения треугольника в квадрате

На фигурах 2, 6, 10 треугольник катится по поверхности окружности, на фигурах 4, 8, 12 треугольник переваливается через вершину, на остальных фигурах происходит смена характера движения треугольника с качения на переваливание и наоборот. Рассмотрим движение вершины треугольника. На фигурах 1, 2, 3 помеченная вершина движется линейно, по прямой (Рис. 10). Фактически помеченная вершина является центром вращения окружности, элементом которой является поверхность стороны треугольника Рело. На фигуре 3 помеченная вершина меняет траекторию движения с прямолинейной на траекторию движения по окружности с радиусом, равным длине стороны, по которой он движется на фигурах 3, 4, 5.

На фигуре 5 происходит смена траектории движения вершины. На фигурах 5, 6, 7 вершина движется по трохоиде точки, находящейся на поверхности окружности с радиусом, равным длине стороны треугольника. На фигурах 7, 8, 9 меченная вершина является точкой перевала треугольника, она жестко лежит на поверхности. Фигуры 9, 10, 11 – опять трохоида и 11, 12, 1 – движение по окружности. По аналогии эти фигуры описаны выше. Меченая вершина возвращается в исходную точку. Треугольник Рело совершил полный оборот.

Рис 8. Движение вершины треугольника Рис 9 Движение центра треугольника.

Фигура постоянной ширины может вращаться в квадрате со стороной всё время касаясь каждой из сторон.

7. Любую плоскую фигуру диаметра можно накрыть фигурой постоянной ширины

Вывод: первоначально выдвинутая гипотеза о том, что треугольник Рело будет сочетать в себе свойства круга и равностороннего треугольника, а также характеризуется только ему присущими свойствами, подтверждена в ходе исследования.

История изобретения треугольника Рело

Треугольник Рело назван по имени Франца Рело – немецкого учёного-инженера, подробно исследовавшего его. Рело дал определение кинематической пары, кинематической цепи и механизма как кинематической цепи принуждённого движения; предложил способ преобразования механизмов путём изменения стойки и путём изменения конструкций кинематических пар. Связал теорию механизмов и машин с проблемами конструирования, например, впервые поставил и пытался решить проблему эстетичности технических объектов.

Однако, впервые эта фигура встречается XV веке в трудах Леонардо да Винчи, созданная им карта мира имеет вид четырех сферических треугольников, которые были показаны на плоскости карты треугольниками Рело, собранными по четыре вокруг полюсов.

Позднее, в XVIII веке встречается идея построения треугольника в трудах Леонардо Эйлера.

Применение треугольника Рело

Применение треугольника Рело основано на его свойствах. Основные сферы применения в технике: сверло Уаттса (сверление квадратных отверстий), роторно-поршневой двигатель Ванкеля (внутри примерно цилиндрической камеры по сложной траектории движется трёхгранный ротор-поршень – треугольник Рело), грейферный механизм в кинопроекторах (используется свойство вращения треугольника Рело в квадрате со стороной ), кулачковые механизмы паровых двигателей, швейных машин и часовых механизмов, катки для транспортировки тяжелых грузов, крышки для люков (свойство постоянной ширины), в качестве медиатора. Кроме того, еще с XIII века используется свойство симметричности и гармонии в архитектурных сооружениях на основе стрельчатых арок и элементов орнамента.

Применение в некоторых механических устройствах

В 1914 году английский инженер Гарри Джеймс Уаттс изобрёл инструмент для сверления квадратных отверстий (рис.), с 1916 года сверла находятся в серийном производстве. Сверло Уаттса представляет собой треугольник Рело, в котором заточены ржущие кромки и прорезаны углубления для отвода стружки.

Рис. 10 Сверло Уаттса и двигатель Ванкеля

Видео:8 класс, 2 урок, Выпуклый многоугольникСкачать

Применение в автомобильных двигателях

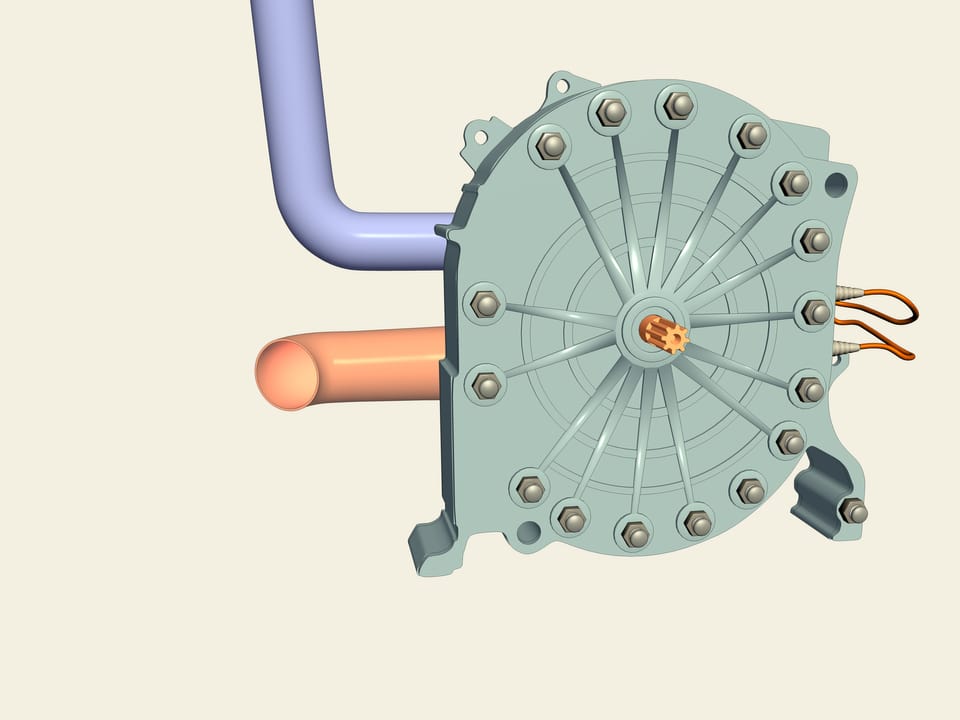
Треугольник Рело используется и в автомобильных двигателях (рис.,). В 1957 году немецкий инженер, изобретатель Ф. Ванкель, сконструировал роторно-поршневой двигатель. Внутри примерно цилиндрической камеры по сложной траектории движется трёхгранный ротор-поршень – треугольник Рело. Он вращается так, что три его вершины находятся в постоянном контакте с внутренней стенкой корпуса, образуя три замкнутых объёма, или камеры сгорания.

Фактически каждая из трёх боковых поверхностей ротора действует как поршень. При всех достоинствах РПД — компактности, приемистости, отсутствии кривошипно-шатунного и газораспределительного механизмов, а так же значительно меньших габаритов и массе при одинаковой с поршневыми двигателями внутреннего сгорания мощности, он имеет и ряд серьезных недостатков: часто выходящие из строя уплотнительные элементы, плохая приспосабливаемость к изменениям внешней нагрузки, повышенный расход топлива и неудовлетворительные показатели по выбросам в отработавших газах. Тем не менне в серийном производстве находятся автомобили Mazda RX-8.

Поиски альтернативных видов топлива для автомобилей заставил вновь обратить внимание на роторно-поршневой двигатель Ванкеля. Разработчики Mazda уверяют, что по природе своей роторно-поршневой агрегат гораздо лучше приспособлен для работы на водороде, нежели традиционные моторы. Впрочем, по прогнозам специалистов, уже к 2025 году более четверти мирового автопарка будет использовать в качестве топлива водород. Так что возможно, будущее за РПД

Применение треугольника Рело в грейферном механизме в кинопроекторах

Устройство грейферного механизма основано на треугольнике Рело, вписанном в квадрат и двойном параллелограмме, который не дает квадрату наклоняться в стороны. Действительно, т. к. длины противоположных сторон равны, то среднее звено при всех движениях остается параллельным основанию, а сторона квадрата всегда параллельной среднему звену. Чем ближе ось крепления к вершине треугольника Рело, тем более близкую к квадрату фигуру описывает зубчик грейфера. Такой механизм обеспечивает равномерное вращение оси, чтобы на экране было четкое изображение, пленку мимо объектива надо протянуть на один кадр, дать ей постоять, потом опять резко протянуть и так 18 раз в секунду.

Крышки для люков

В форме треугольника Рёло можно изготавливать крышки для люков — опытным путем доказано, что благодаря постоянной ширине они не могут провалиться в люк. В Сан-Франциско, для системы рекуперирования воды корпуса люков имеют форму треугольника Рёло. Зак счет того, что у треугольника Рело площадь меньше, чем у круга, себестоиморсть люков в форме треугольников Рело была бы ниже, чем у традиционно круглых. Перейдя на серийное производство люклв в форме треугольника Рело, на мой взгляд, можно было бы быстрее решить проблему открытых колодцев и избежать травматизма и смертей людей.

Видео:Геометрия 7 класс (Урок№24 - Соотношения между сторонами и углами треугольника. Неравенство треуг.)Скачать

Треугольник Рёло в искусстве, архитектуре и литературе

Форма треугольника Рёло, его свойство симметричности, используется и в архитектурных целях. Конструкция из двух его дуг образует характерную для готического стиля стрельчатую арку, однако целиком он встречается в готических сооружениях довольно редко. Окна в форме треугольника Рёло использовали еще в VIII векев церкви Богоматери в Брюгге, а также в шотландской церкви в Аделаиде. Как элемент орнамента он встречается на оконных решётках цистерцианского аббатства в швейцарской коммуне Отрив (приложение 1)

Треугольник Рёло используют и в архитектуре, не принадлежащей к готическому стилю. Например, построенная в 2006 году в Кёльне 103-метровая башня под названием «Кёльнский треугольник» в сечении представляет собой именно эту фигуру.

В научно-фантастическом рассказе Пола Андерсона «Треугольное колесо» экипаж землян совершил аварийную посадку на планете, население которой не использовало колёса, так как всё круглое находилось под религиозным запретом. В сотнях километров от места посадки предыдущая земная экспедиция оставила склад с запасными частями, но перенести оттуда необходимый для корабля двухтонный атомный генератор без каких-либо механизмов было невозможно. В итоге землянам удалось соблюсти табу и перевезти генератор, используя катки с сечением в виде треугольника Рёло.

Изобретение велосипеда с треугольными колесами

Колесо, изобретенное несколько тысяч лет назад, произвело переворот в жизни человека. Постоянство ширины явилось для колеса определяющим свойством, следствием которого явилось техническое завоевание мира.

Изобретением колес велосипеда занимается китайский рационализатор Гуань Байхуа (Guan Baihua), 50-летний офицер из города Циндао. Больше того, он изобретает заново самую консервативную деталь велосипеда – колеса. Вместо понятных всем круглых он предложил кататься на колесах пяти — и треугольной формы (спереди и сзади, соответственно). Для китайцев велосипед – главный вид транспорта, популярностью затмевающий автомобили. Но велосипед с угловатыми колесами средством передвижения не станет. По словам изобретателя, поездка на нем требует больше усилий, чем на обычном велосипеде, и скорее всего, он найдет свою нишу в качестве экзотической игрушки и более эффективного тренажера. Впрочем, все, кто пробовал прокатиться на нем, удивляются вовсе не трудности кручения педалей, а неожиданной плавности хода.
Действительно, казалось бы, угловатые колеса неизбежно должны создавать при качении существенную тряску – но ее Гуаню Байхуа удалось снизить благодаря прекрасному знанию геометрии и настоящей китайской хитрости. .

Таким же образом можно устроить подвеску некруглого колеса и взяв четыре таких подвески, можно соорудить повозку. При этом она будет ехать совершенно без покачиваний! Чтоьы убедиться, что тряски нет, можно поставить, как учат автомобилистские традиции, на тележку стакан с водой.

Рисунок 11 Повозка с «треугольными» колесами.

Мы попробовали соорудить такую повозку и опытным путем проверить гипотезу об отсутствии качки.

Рисунок 12 «Треугольные» колеса.

Рисунок 13 Варианты повозки с «треугольными» колесами. Результаты эксперимента подтвердили нашу гипотезу.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Заключение

Несколько тысяч лет назад было изобретено колесо, которое произвело переворот в жизни человека. Определяющим свойством, следствием которого стало техническое завоевание мира, стало свойство постоянства ширины. Но, как оказалось, круг – не единственная фигура, которая обладает этим свойством. Вызвавший мой интерес, треугольник Рело, также принадлежит этому семейству.

В своей работе мы не только изучили его свойства, геометрические характеристики, историю изобретения, но и рассмотрели сферы применения этой выпуклой, симметричной фигуры постоянной ширины. Выдвинутая нами гипотеза о свойствах этой фигуры нашла свое подтверждение. Кроме того, мы ответили для себя на ряд вопросов познавательного характера: какие геометрические свойства обеспечивают плавность хода велосипеда с «треугольными» колесами, почему канализационные люки делают круглыми или в форме треугольника Рело?

Не менее познавательной оказалась информация о сферах применения «круглого» треугольника не только в технике, но и в архитектуре, литературе.

Таким образом, поставленные мною задачи, реализованы в полном объеме.

Перспективы дальнейшей работы в этом направлении:

1. Лежащую в основе треугольника Рело, идею построения можно обобщить для построения многоугольников Рело, используя для создания кривых постоянной ширины, не равносторонний треугольник, а звёздчатый многоугольник, образованный отрезками прямых равной длины.

2. Изучение свойств тел постоянной ширины.

Список источников информации и иллюстраций:

1. Велосипед с треугольным колесом// Материал сайта Веломастерская «Две звезды» [Электронный ресурс] — Режим доступа. — URL: http://*****/news/velosiped-s-treugolnyim-kolesom. html

Видео:Многоугольники. Математика 8 класс | TutorOnlineСкачать

2. Треугольник Рёло// Материал из Википедии — свободной энциклопедии

[Электронный ресурс] — Режим доступа. — URL: http://ru. wikipedia. org/wiki/

3. Бронштейн, И. Н., Семендяев, К. А., Справочник по математике для инженеров и учащихся вузов.// – М.:Просвещение,1992.

4. Коксетер, С. М., Грейтцер, С. Л., Новые встречи с геометрией. //– М., Наука, 1978.-223с.

5. Конфорович, А. Г., Некоторые математические задачи//. – Киев, Родная школа, 1981.-189с.

6. Числа и фигуры — М., Физматгиз, 19с.

7. , Болтянский постоянной ширины // Выпуклые фигуры. — М.—Л.: ГТТИ, 1951. — С. 90—105. — 343 с.

Сайты в Интернете:

1. http://ru. wikipedia. org/wiki/%D0%A2%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA_%D0%A0%D1%91%D0%BB%D0%BE

2. http://www. *****/article/5480-kolesa-s-uglami/

3. http://www. *****/ru/etudes/mazda/

1. http://www. *****/images/upload/article/bike_1__preview2.jpg

2. http://www. *****/images/upload/article/bike_2__preview2.jpg

3. http://upload. wikimedia. org/wikipedia/commons/thumb/9/9b/Leonardo_da_Vinci%E2%80%99s_Mappamundi. jpg/220px-Leonardo_da_Vinci%E2%80%99s_Mappamundi. jpg

4. http://upload. wikimedia. org/wikipedia/commons/thumb/b/b2/Reuleaux_triangle%2C_incircle_and_circumcircle. svg/250px-Reuleaux_triangle%2C_incircle_and_circumcircle. svg. png

5. http://upload. wikimedia. org/wikipedia/commons/2/22/Rotation_of_Reuleaux_triangle. gif

6. http://upload. wikimedia. org/wikipedia/commons/thumb/2/2a/Luch2_greifer. gif/220px-Luch2_greifer. gif

7. http://upload. wikimedia. org/wikipedia/commons/thumb/b/bc/Manhole_cover_for_reclaimed_water_SFWD. JPG/220px-Manhole_cover_for_reclaimed_water_SFWD. JPG

8. http://upload. wikimedia. org/wikipedia/commons/thumb/d/d0/Reuleaux_triangles_on_a_window_of_Onze-Lieve-Vrouwekerk%2C_Bruges_2.jpg/450px-Reuleaux_triangles_on_a_window_of_Onze-Lieve-Vrouwekerk%2C_Bruges_2.jpg

9. http://upload. wikimedia. org/wikipedia/commons/thumb/2/21/Reuleaux_triangle_shaped_window_of_Sint-Salvatorskathedraal%2C_Bruges. jpg/125px-Reuleaux_triangle_shaped_window_of_Sint-Salvatorskathedraal%2C_Bruges. jpg

10. http://upload. wikimedia. org/wikipedia/commons/thumb/3/35/Reuleaux_triangles_on_a_window_of_Saint_Michael_church%2C_Luxembourg. jpg/800px-Reuleaux_triangles_on_a_window_of_Saint_Michael_church%2C_Luxembourg. jpg

11. http://upload. wikimedia. org/wikipedia/commons/thumb/9/9c/K%C3%B6lnTriangle_%28Flight_over_Cologne%29.jpg/125px-K%C3%B6lnTriangle_%28Flight_over_Cologne%29.jpg

12. http://upload. wikimedia. org/wikipedia/commons/thumb/e/eb/Reuleaux_triangles_on_a_window_of_Sint-Baafskathedraal%2C_Ghent_2.jpg/125px-Reuleaux_triangles_on_a_window_of_Sint-Baafskathedraal%2C_Ghent_2.jpg

13. http://upload. wikimedia. org/wikipedia/commons/thumb/4/4a/Reuleaux_triangle_shaped_window_of_Onze-Lieve-Vrouwekerk%2C_Bruges. jpg/125px-Reuleaux_triangle_shaped_window_of_Onze-Lieve-Vrouwekerk%2C_Bruges. jpg

Использование треугольника Рело в архитектуре