Найдите на числовой окружности точку 11п 6

Надеюсь, вы уже прочитали про числовую окружность и знаете, почему она называется числовой, где на ней начало координат и в какой стороне положительное направление. Если нет, то бегом читать ! Если вы, конечно, собираетесь находить точки на числовой окружности.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Обозначаем числа (2π), (π), (frac), (-frac), (frac)

Как вы знаете из прошлой статьи, радиус числовой окружности равен (1). Значит, длина окружности равняется (2π) (вычислили по формуле (l=2πR)). С учетом этого отметим (2π) на числовой окружности. Чтобы отметить это число нужно пройти от (0) по числовой окружности расстояние равно (2π) в положительном направлении, а так как длина окружности (2π), то получается, что мы сделаем полный оборот. То есть, числу (2π) и (0) соответствует одна и та же точка. Не переживайте, несколько значений для одной точки — это нормально для числовой окружности.

Теперь обозначим на числовой окружности число (π). (π) – это половина от (2π). Таким образом, чтобы отметить это число и соответствующую ему точку, нужно пройти от (0) в положительном направлении половину окружности.

Отметим точку (frac) . (frac) – это половина от (π), следовательно чтобы отметить это число, нужно от (0) пройти в положительном направлении расстояние равное половине (π), то есть четверть окружности.

Обозначим на окружности точки (-) (frac) . Двигаемся на такое же расстояние, как в прошлый раз, но в отрицательном направлении.

Нанесем (-π). Для этого пройдем расстояние равное половине окружности в отрицательном направлении.

Теперь рассмотрим пример посложнее. Отметим на окружности число (frac) . Для этого дробь (frac) переведем в смешанный вид (frac) (=1) (frac) , т.е. (frac) (=π+) (frac) . Значит, нужно от (0) в положительную сторону пройти расстояние в пол окружности и еще в четверть.

Задание 1. Отметьте на числовой окружности точки (-2π),(-) (frac) .

Видео:Как искать точки на тригонометрической окружности.Скачать

Обозначаем числа (frac), (frac), (frac)

Выше мы нашли значения в точках пересечения числовой окружности с осями (x) и (y). Теперь определим положение промежуточных точек. Для начала нанесем точки (frac) , (frac) и (frac) .
(frac) – это половина от (frac) (то есть, (frac) (=) (frac) (:2)) , поэтому расстояние (frac) – это половина четверти окружности.

(frac) – это треть от (π) (иначе говоря, (frac) (=π:3)), поэтому расстояние (frac) – это треть от полукруга.

(frac) – это половина (frac) (ведь (frac) (=) (frac) (:2)) поэтому расстояние (frac) – это половина от расстояния (frac) .

Вот так они расположены друг относительно друга:

Замечание: Расположение точек со значением (0), (frac) ,(π), (frac) , (frac) , (frac) , (frac) лучше просто запомнить. Без них числовая окружность, как компьютер без монитора, вроде бы и полезная штука, а использовать крайне неудобно.

Разные расстояние на окружности наглядно:

Видео:Точки на числовой окружностиСкачать

Обозначаем числа (frac), (-frac), (frac)

Обозначим на окружности точку (frac) , для этого выполним следующие преобразования: (frac) (=) (frac) (=) (frac) (+) (frac) (=π+) (frac) . Отсюда видно, что от нуля в положительную сторону надо пройти расстояние (π), а потом еще (frac) .

Отметим на окружности точку (-) (frac) . Преобразовываем: (-) (frac) (=-) (frac) (-) (frac) (=-π-) (frac) . Значит надо от (0) пройти в отрицательную сторону расстояние (π) и еще (frac) .

Нанесем точку (frac) , для этого преобразуем (frac) (=) (frac) (=) (frac) (-) (frac) (=2π-) (frac) . Значит, чтобы поставить точку со значением (frac) , надо от точки со значением (2π) пройти в отрицательную сторону расстояние (frac) .

Видео:№ 4.6- Алгебра 10-11 класс МордковичСкачать

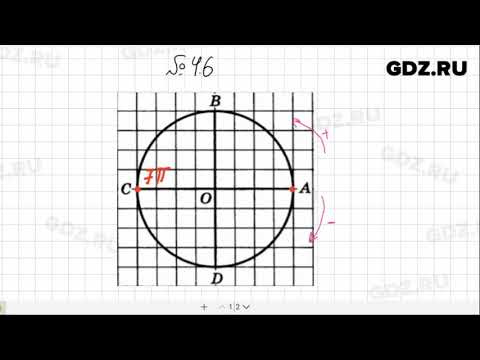
Обозначаем числа (10π), (-3π), (frac) ,(frac), (-frac), (-frac)

Запишем (10π) в виде (5 cdot 2π). Вспоминаем, что (2π) – это расстояние равное длине окружности, поэтому чтобы отметить точку (10π), нужно от нуля пройти расстояние равное (5) окружностям. Нетрудно догадаться, что мы окажемся снова в точке (0), просто сделаем пять оборотов.

Из этого примера можно сделать вывод:

Числам с разницей в (2πn), где (n∈Z) (то есть (n) — любое целое число) соответствует одна и та же точка.

То есть, чтобы поставить число со значением больше (2π) (или меньше (-2π)), надо выделить из него целое четное количество (π) ((2π), (8π), (-10π)…) и отбросить. Тем самым мы уберем из числа, не влияющие на положение точки «пустые обороты».

Точке, которой соответствует (0), также соответствуют все четные количества (π) ((±2π),(±4π),(±6π)…).

Теперь нанесем на окружность (-3π). (-3π=-π-2π), значит (-3π) и (–π) находятся в одном месте на окружности (так как отличаются на «пустой оборот» в (-2π)).

Кстати, там же будут находиться все нечетные (π).

Точке, которой соответствует (π), также соответствуют все нечетные количества (π) ((±π),(±3π),(±5π)…).

Сейчас обозначим число (frac) . Как обычно, преобразовываем: (frac) (=) (frac) (+) (frac) (=3π+) (frac) (=2π+π+) (frac) . Два пи – отбрасываем, и получается что, для обозначения числа (frac) нужно от нуля в положительную сторону пройти расстояние равное (π+) (frac) (т.е. половину окружности и еще четверть).

Отметим (frac) . Вновь преобразования: (frac) (=) (frac) (=) (frac) (+) (frac) (=5π+) (frac) (=4π+π+) (frac) . Ясно, что от нуля надо пройти расстояние равное (π+) (frac) – и мы найдем место точки (frac) .

Нанесем на окружность число (-) (frac) .
(-) (frac) (= -) (frac) (-) (frac) (=-10π-) (frac) . Значит, место (-) (frac) совпадает с местом числа (-) (frac) .

Обозначим (-) (frac) .
(-) (frac) (=-) (frac) (+) (frac) (=-5π+) (frac) (=-4π-π+) (frac) . Для обозначение (-) (frac) , на числовой окружности надо от точки со значением (–π) пройти в положительную сторону (frac) .

Видео:Алгебра 10 класс. 20 сентября. Числовая окружность #6 координаты точекСкачать

Единичная числовая окружность на координатной плоскости

п.1. Понятие тригонометрии

Тригонометрия берёт своё начало в Древней Греции. Само слово «тригонометрия» по-гречески означает «измерение треугольников». Эта наука в течение тысячелетий используется землемерами, архитекторами и астрономами.
Начиная с Нового времени, тригонометрия заняла прочное место в физике, в частности, при описании периодических процессов. Например, переменный ток в розетке генерируется в периодическом процессе. Поэтому любой электрический или электронный прибор у вас в доме: компьютер, смартфон, микроволновка и т.п., — спроектирован с использованием тригонометрии.

Базовым объектом изучения в тригонометрии является угол.

Предметом изучения тригонометрии как раздела математики выступают:
1) взаимосвязи между углами и сторонами треугольника, которые называют тригонометрическими функциями;
2) использование тригонометрических функций в геометрии.

п.2. Числовая окружность

Мы уже знакомы с числовой прямой (см. §16 справочника для 8 класса) и координатной плоскостью (см. §35 справочника для 7 класса), с помощью которых создаются графические представления числовых промежутков и функций. Это удобный инструмент моделирования, с помощью которого можно провести анализ, начертить график, найти область допустимых значений и решить задачу.
Для работы с углами и их функциями существует аналогичный инструмент – числовая окружность.

Числовая окружность (тригонометрический круг) – это окружность единичного радиуса R=1 с центром в начале координат (0;0). Точка с координатами (1;0) является началом отсчета , ей соответствует угол, равный 0. Углы на числовой окружности отсчитываются против часовой стрелки. Направление движения против часовой стрелки является положительным ; по часовой стрелке – отрицательным .

Отметим на числовой окружности углы 30°, 45°, 90°, 120°, 180°, а также –30°, –45°, –90&deg, –120°, –180°.

п.3. Градусная и радианная мера угла

Углы можно измерять в градусах или в радианах.
Известно, что развернутый угол, дуга которого равна половине окружности, равен 180°. Прямой угол, дуга которого равна четверти окружности, равен 90°. Тогда полная, замкнутая дуга окружности составляет 360°.
Приписывание развернутому углу меры в 180°, а прямому 90°, достаточно произвольно и уходит корнями в далёкое прошлое. С таким же успехом это могло быть 100° и 50°, или 200° и 100° (что, кстати, предлагалось одним из декретов во времена французской революции 1789 г.).

В целом, более обоснованной и естественной для измерения углов является радианная мера.

Найдем радианную меру прямого угла ∠AOB=90°. Построим окружность произвольного радиуса r с центром в вершине угла – точке O. Длина этой окружности: L=2πr. Длина дуги AB: (l_=frac=frac=frac.) Тогда радианная мера угла: $$ angle AOB=frac<l_>=frac=frac $$

п.4. Свойства точки на числовой окружности

Построим числовую окружность. Обозначим O(0;0), A(1;0)

Каждому действительному числу t на числовой окружности соответствует точка Μ(t). При t=0, M(0)=A. При t>0 двигаемся по окружности против часовой стрелки, описывая дугу ⌒ AM=t. Точка M — искомая. При t Например:

Отметим на числовой окружности точки, соответствующие (frac, frac, frac, frac, pi), а также (-frac, -frac, -frac, -frac, -pi) Для этого нужно отложить углы 30°, 45°, 90°, 120°, 180° и –30°, –45°, –90°, –120°, –180° с вершиной в начале координат и отметить соответствующие дуги на числовой окружности.

Отметим на числовой окружности точки, соответствующие (frac, frac, frac), и (-frac). Все четыре точки совпадают, т.к. begin Mleft(fracright)=Mleft(frac+2pi kright)\ frac-2pi=-frac\ frac+2pi=frac\ frac+4pi=frac end

п.5. Интервалы и отрезки на числовой окружности

Каждому действительному числу соответствует точка на числовой окружности. Соответственно, числовые промежутки (см. §16 справочника для 8 класса) получают свои отображения в виде дуг.

Числовой промежуток	Соответствующая дуга числовой окружности
Отрезок
$$ -frac lt t lt frac $$ а также, с учетом периода $$ -frac+2pi klt tltfrac+2pi k $$
Интервал
$$ -frac leq t leq frac $$ а также, с учетом периода $$ -frac+2pi kleq tleqfrac+2pi k $$
Полуинтервал
$$ -frac leq t ltfrac $$ а также, с учетом периода $$ -frac+2pi kleq tltfrac+2pi k $$

п.6. Примеры

Пример 1. Точка E делит числовую окружность во второй четверти в отношении 1:2.
Чему равны дуги AE, BE, EC, ED в градусах и радианах?

Угловая мера четверти 90°. При делении в отношении 1:2 получаем дуги 30° и 60° соответственно: begin BE=30^=frac.\ EC=60^=frac.\ AE=EC+CD=90^+30^=120^=frac.\ ED=EC+CD=60^+90^=150^=frac. end

Пример 2. Найдите на числовой окружности точку, соответствующую данному числу: (-frac; frac; frac; frac).

Находим соответствующие углы в градусах и откладываем с помощью транспортира (положительные – против часовой стрелки, отрицательные – по часовой стрелке), отмечаем соответствующие точки на числовой окружности. begin -frac=-90^, frac=135^\ frac=210^, frac=315^ end

Пример 3. Найдите на числовой окружности точку, соответствующую данному числу: (-frac; 5pi; frac; frac).

Выделяем из дроби целую часть, отнимаем/прибавляем один или больше полных оборотов (2πk — четное количество π), чтобы попасть в промежуток от 0 до 2π. Далее – действуем, как в примере 2. begin -frac=fraccdotpi=-6pi+fracrightarrow frac=90^\ 5pi=4pi+pirightarrow pi=180^\ frac=fracpi=3pi-fracrightarrow pi-frac=frac\ frac=fracpi=7pi-fracrightarrow pi-frac=frac end

Пример 4. В какой четверти числовой окружности находится точка, соответствующая числу: 2; 4; 5; 7.

Сравниваем каждое число с границами четвертей: begin 0, fracpi2approxfrac=1,57, piapprox 3,14\ 3pi 3cdot 3,14\ fracapprox frac=4,71, 2piapprox 6,28 end

(fracpi2lt 2lt pi Rightarrow ) угол 2 радиана находится во 2-й четверти
(pilt 4lt frac Rightarrow ) угол 4 радиана находится в 3-й четверти
(fraclt 5lt 2pi Rightarrow ) угол 5 радиана находится в 4-й четверти
(7gt 2pi), отнимаем полный оборот: (0lt 7-2pilt fracpi2Rightarrow) угол 7 радиан находится в 1-й четверти.

Пример 5. Изобразите на числовой окружности множество точек ((kinmathbb)), запишите количество полученных базовых точек.

$$ frac $$	$$ -frac+2pi k $$
Четыре базовых точки, через каждые 90°	Две базовых точки, через каждые 180°
$$ frac+frac $$	$$ -frac $$
Три базовых точки, через каждые 120°	Пять базовых точек, через каждые 72°

Пример 6. Изобразите на числовой окружности дуги, соответствующие числовым промежуткам.

Видео:Координаты точек на числовой окружности, часть 5. Алгебра 10 класс.Скачать

Найдите на числовой окружности точку которая соответствует заданному числу п / 6?

Алгебра | 10 — 11 классы

Найдите на числовой окружности точку которая соответствует заданному числу п / 6.

Sin1 2 и cos кореня из 3 2.

Видео:Координаты точек на числовой окружности, часть 6. Алгебра 10 класс.Скачать

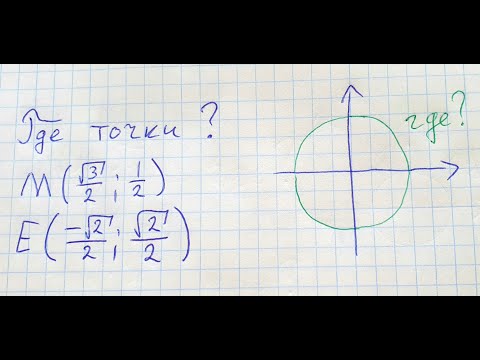
Найдите на числовой окружности все точки с абсциссой или ординатой, удовлетворяющей заданному неравенству или системе неравенств, и запишите ( с помощью неравенства), каким числам t они соответствуют ?

Найдите на числовой окружности все точки с абсциссой или ординатой, удовлетворяющей заданному неравенству или системе неравенств, и запишите ( с помощью неравенства), каким числам t они соответствуют :

Видео:Соответствие чисел точкам числовой окружностиСкачать

Найти на числовой окружности точку которая соответсвует заданному числу подробно 4П / 3?

Найти на числовой окружности точку которая соответсвует заданному числу подробно 4П / 3.

Видео:Как найти координаты точек на тригонометрической окружностиСкачать

Найдите на числовой окружности точку, которая соответствует числу п / 3, п / 4, п / 6, п / 8?

Найдите на числовой окружности точку, которая соответствует числу п / 3, п / 4, п / 6, п / 8.

Видео:Числовая окружностьСкачать

На числовой окружности взяты точки M(2п / 3), N(п / 4) / Найдите все числа t, которым на данной окружности соответствуют точки, принадлежащие дуге MN?

На числовой окружности взяты точки M(2п / 3), N(п / 4) / Найдите все числа t, которым на данной окружности соответствуют точки, принадлежащие дуге MN.

Видео:Определение значений по точкам на числовой окружностиСкачать

Найдите на числовой окружности точки с данной ординатой y = 0, 5, и запишите, каким числам t они соответствуют?

Найдите на числовой окружности точки с данной ординатой y = 0, 5, и запишите, каким числам t они соответствуют.

Видео:Косинус на числовой окружности. Алгебра 10 класс.Скачать

Как найти на числовой окружности точки?

Как найти на числовой окружности точки.

Которые соответствуют числам 4, 5 и — 3?

Какой четверти числовой окружности принадлежат точки, соответствующих числам 8, 4 , 3, и — 8?

Видео:Числовая окружностьСкачать

Найти на числовой окружности точки, соответствующие числам 1 ; — 2 ; 3?

Найти на числовой окружности точки, соответствующие числам 1 ; — 2 ; 3.

Видео:Тригонометрическая окружность. Как выучить?Скачать

Найдите все числа, которым соответствуют отмеченные на числовой окружности точки?

Найдите все числа, которым соответствуют отмеченные на числовой окружности точки.

Видео:Координаты точек на числовой окружности, часть 3. Алгебра 10 класс.Скачать

1 ) Найдите на числовой окружности точку, которая соответствует заданному числу — / 22 ) Найдите на числовой окружности все точки M(t), соответствующие заданной формуле ( во всех формулах предпологает?

1 ) Найдите на числовой окружности точку, которая соответствует заданному числу — / 2

2 ) Найдите на числовой окружности все точки M(t), соответствующие заданной формуле ( во всех формулах предпологаеться , что n принадлежит Z

Видео:Длина дуги числовой окружности | Алгебра 10 класс #9 | ИнфоурокСкачать

Сроочно?

Найдите на числовой окружности точку , которая соотвествует заданному числу а) 2п б)п / 3 в)5п / 6 г)7п / 2.

На этой странице сайта вы найдете ответы на вопрос Найдите на числовой окружности точку которая соответствует заданному числу п / 6?, относящийся к категории Алгебра. Сложность вопроса соответствует базовым знаниям учеников 10 — 11 классов. Для получения дополнительной информации найдите другие вопросы, относящимися к данной тематике, с помощью поисковой системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям. Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы помогут найти нужную информацию.

Все примеры построены по одной схеме и решаются одинаково : 1) ( — 5a — 3b)²( — 5a + 3b) = — 125a³ — 75a²b + 45ab² + 27b³ 2) ( — 7a — 6b)²( — 7a + 6b) = — 343a³ — 294a²b + 252ab² + 216b³ 3) ( — 3a — 7b)²( — 3a + 7b) = — 27a³ — 63a²b + 147ab² + 343b..

0, 1(2) = 12 — 1 = 11 / 90 90 1, 12(3) = 1 123 — 12 = 1 111 / 900 900 7, 5(4) = 7 54 — 5 = 7 49 / 90 90 8, 7(21) = 8721 — 7 = 8 714 / 990 = 8 119 / 165 990 вроде так.

600 рублей — 100% x — 10% x = 60 600 — 60 = 540рублей — стал стоить чайник после первого снижения. 540 — 100% x — 20% x = 108 600 — 108 = 492 рубля — стал стоить чайник после второго снижения. Ответ : 492.

Смотри рисунок в вложении ВС = d = 2r = 2 * 43 = 86 см — диаметр окружности ∠CAB — вписанный, опирается на диаметр окружности→∠CAB = 180 : 2 = 90° ЗначитΔАВС — прямоугольный АС = ВС * sin30 = BC * 0, 5 = 85 * 0, 5 = 43 cm Ответ 43 см.

Угол ACB = 30 Радиус 43 Угол AOB = 60 — как центральный. Значит треугольник AOB — равносторонний, потому что AO = OB = AB = 43, а так же углы равны по 60 AB = 43.

📽️ Видео

10 класс. Числовая окружность на координатной плоскости.Скачать

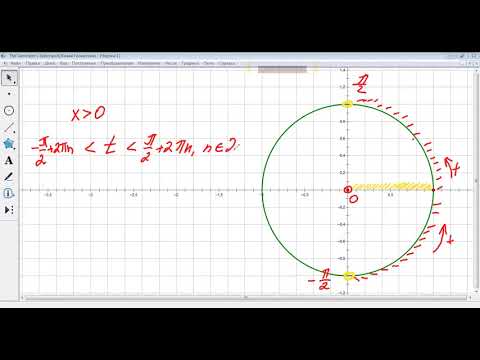
Координаты точек на числовой окружности, часть 2. Алгебра 10 класс.Скачать

10 класс, 12 урок, Числовая окружность на координатной плоскостиСкачать

1. Числовая окружность. 10 классСкачать