- Онлайн калькулятор
- Как посчитать длину хорды (градусы)
- Как посчитать длину хорды (радианы)
- Теория
- Формула
- Пример
- Формула длины хорды окружности
- Две окружности на плоскости. Общие касательные к двум окружностям
- Взаимное расположение двух окружностей
- Формулы для длин общих касательных и общей хорды двух окружностей
- Доказательства формул для длин общих касательных и общей хорды двух окружностей
- 📹 Видео
Видео:ОГЭ ЗАДАНИЕ 16 НАЙДИТЕ ДЛИНУ ХОРДЫ ОКРУЖНОСТИ ЕСЛИ РАДИУС 13 РАССТОЯНИЕ ДО ХОРДЫ 5Скачать
Онлайн калькулятор
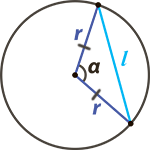
Хорда круга – отрезок соединяющий две точки, лежащие на окружности.
Чтобы посчитать длину хорды вам необходимо знать, чему равен радиус (r) окружности и угол (α) между двумя радиусами, образующими вместе с хордой равнобедренный треугольник (см. рис.)
Как посчитать длину хорды (градусы)
Чему равна длина хорды окружности если её радиус ,
а
Как посчитать длину хорды (радианы)
Чему равна длина хорды окружности если её радиус ,
а
Видео:Расчет сегмента окружности по хорде и длине цилиндрической поверхности (трансцендентное уравнение)Скачать
Теория
Чему равна длина хорды (l) окружности если известны её радиус (r) и центральный угол (α), опирающийся на данную хорду?
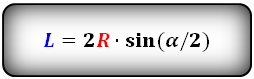
Формула
Пример
Если радиус круга равен 4 см, а ∠α = 90°, то длина хорды примерно равна 5.65 см.
Видео:Длина окружности. Математика 6 класс.Скачать
Формула длины хорды окружности
Хорда — отрезок соединяющий любые две точки окружности. Диаметр окружности, самая большая хорда.
L — хорда
R — радиус окружности
O — центр окружности
α — центральный угол
Формула длины хорды, ( L ):
Калькулятор для расчета длины хорды окружности :
Дополнительные формулы для окружности:
Видео:ЕГЭ-2022 ||Задание №6 || Найти длину хордыСкачать
Две окружности на плоскости.
Общие касательные к двум окружностям
 Взаимное расположение двух окружностей |
| Общие касательные к двум окружностям |
| Формулы для длин общих касательных и общей хорды |
| Доказательства формул для длин общих касательных и общей хорды |
Видео:Длина окружности. Площадь круга. 6 класс.Скачать
Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |  | |
| Каждая из окружностей лежит вне другой |  | |
| Внешнее касание двух окружностей |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  |  |
| Каждая из окружностей лежит вне другой | ||
| ||
| Внешнее касание двух окружностей | ||
| ||
| Внутреннее касание двух окружностей | ||
| ||
| Окружности пересекаются в двух точках | ||
| ||
| ||
| Каждая из окружностей лежит вне другой | ||
Расстояние между центрами окружностей больше суммы их радиусов | ||
| Внешнее касание двух окружностей | ||
Расстояние между центрами окружностей равно сумме их радиусов | ||
| Внутреннее касание двух окружностей | ||
| Окружности пересекаются в двух точках | ||
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 лежит внутри другой | ||
| Внутренняя касательная к двум окружностям |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  | |
| Внешнее касание двух окружностей |  | |
 | ||
 | ||
| Внешняя касательная к двум окружностям | |
 | |
| Внутренняя касательная к двум окружностям | |
| |
| Внутреннее касание двух окружностей | |
| |
| Окружности пересекаются в двух точках | |
| |
| Внешнее касание двух окружностей | |
| |
| |
| Каждая из окружностей лежит вне другой | |
| |
| Внешняя касательная к двум окружностям | |||||||||||||||||||||
| Внутренняя касательная к двум окружностям | |||||||||||||||||||||
| Внутреннее касание двух окружностей | |||||||||||||||||||||
| Окружности пересекаются в двух точках | |||||||||||||||||||||
| Внешнее касание двух окружностей | |||||||||||||||||||||
| Каждая из окружностей лежит вне другой | |||||||||||||||||||||
| Фигура | Рисунок | Формула | ||||||||||||
| Внешняя касательная к двум окружностям |  | |||||||||||||
| Внутренняя касательная к двум окружностям |  | |||||||||||||
| Общая хорда двух пересекающихся окружностей |  | |||||||||||||
| Внешняя касательная к двум окружностям | ||||
| ||||
| Внутренняя касательная к двум окружностям | ||||
| ||||
| Общая хорда двух пересекающихся окружностей | ||||
| ||||
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Общая хорда двух пересекающихся окружностей |
Длина общей хорды двух окружностей вычисляется по формуле
Видео:Окружнось. Зависимость длины хорды, от длины дуги.Скачать  Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле
Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, 📹 ВидеоРадиус и диаметрСкачать  Общая хорда двух окружностейСкачать  Всё про углы в окружности. Геометрия | МатематикаСкачать  +Как найти длину окружностиСкачать  Длина хорды окружности равна 72 ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать  Окружность. Длина хорды. Теорема синусов.Скачать  Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать  Деление окружности на равные части. Внимание!!! В таблице имеются ошибки. ПОЛЬЗУЙТЕСЬ ФОРМУЛОЙ!!!Скачать  Как измерить радиус детали по длине хорды и высоте сегментаСкачать  Длина окружности. Площадь круга - математика 6 классСкачать  Геометрия Общая хорда двух пересекающихся окружностей видна из их центров под углами 90 и 60. НайтиСкачать  Задача на нахождение длины хорды окружностиСкачать  Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать  |
