Найдите длину разности векторов a и b изображенных на клетчатой бумаге 1х1 см

Геометрия | 5 — 9 классы

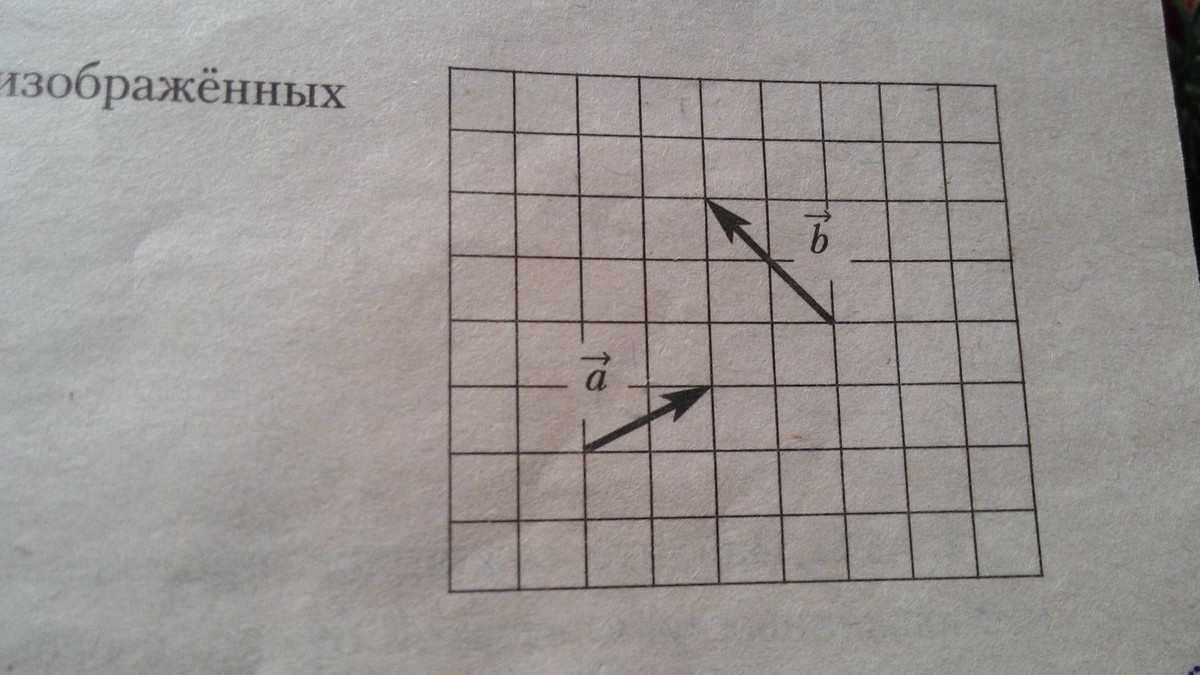
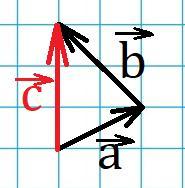
Найдите длину суммы векторов a и b, изображенных на клетчатой бумаге с размером клетки 1 на 1.

Длина $displaystyle vec$ равна 3·1 = 3 т.

К. размер клетки 1 на 1.

Найдите площадь трапеции , изображенной на клетчатой бумаге с размером клетки 1см× 1см Ответ дайте в квадратных см?

Найдите площадь трапеции , изображенной на клетчатой бумаге с размером клетки 1см× 1см Ответ дайте в квадратных см.

Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см х 1 см?

Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см х 1 см.

На клетчатой бумаге с размером клетки 1×1 изоброжена трапеция ?

На клетчатой бумаге с размером клетки 1×1 изоброжена трапеция .

Найдите длину ее средней линии.

На клетчатой бумаге с размером клетки 1х1 изображена трапеция?

На клетчатой бумаге с размером клетки 1х1 изображена трапеция.

Найдите длину её средней линии.

Найдите (в см ^ 2) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см× 1 см?

Найдите (в см ^ 2) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см× 1 см.

Найдите (в см ^ 2) площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1× 1 см?

Найдите (в см ^ 2) площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1× 1 см.

Найдите (в см ^ 22) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см?

Найдите (в см ^ 22) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см.

Найдите (в см ^ 2) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см?

Найдите (в см ^ 2) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см.

Найдите (в см ^ 2) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см?

Найдите (в см ^ 2) площадь многоугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см.

На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник Найдите длину его гипотенузы?

На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник Найдите длину его гипотенузы.

На этой странице вы найдете ответ на вопрос Найдите длину суммы векторов a и b, изображенных на клетчатой бумаге с размером клетки 1 на 1?. Вопрос соответствует категории Геометрия и уровню подготовки учащихся 5 — 9 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.

Векторы на плоскости Работу выполнила Нина Саидзода. — презентация

Презентация была опубликована 8 лет назад пользователемКирилл Самошин

Похожие презентации

Презентация на тему: » Векторы на плоскости Работу выполнила Нина Саидзода.» — Транскрипт:

1 Векторы на плоскости Работу выполнила Нина Саидзода

2 Содержание I.ТеорияТеория II.Задачи на тему: «Векторы на плоскости» Задача 1 Задача 2 Задача 3 III.Проверь себяПроверь себя

3 Теория «Векторы на плоскости» Сложение Правило треугольника Правило параллелограмма Свойство сложения Вычитание Правило трех точек

5 А B C Для любых трех точек А, В и С справедливо равенство:

6 Правило параллелограмма А B C

8 Вычитание векторов Разностью векторов и называется такой вектор, сумма которого с вектором равна вектору

9 Вычитание B A C

10 Правило трех точек Любой вектор можно представить как разность двух векторов, проведенных из одной точки. А B K

11 Задача 1 ОТВЕТ: 3

12 Задача 2 2. Найдите длину суммы векторов и изображенных на клетчатой бумаге с размером клетки 1×1 Ответ: 5

13 Задача 3 3.Найдите длину разности векторов и, изображенных на клетчатой бумаге с размером клетки 1×1 Ответ: 4

14 Упростите выражения: а) б) в) г) Проверь себя показать

Математика ОГЭ-2020. Решение заданий №19 (задания на клетчатой бумаге)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Решение заданий.docx

Решение заданий №19(задания на клетчатой бумаге)

1.Основные типы задач

Определение тангенса угла;

Определение площади фигуры (ромба, трапеции, параллелограмма, треугольника);

Определение расстояния от точки до прямой (отрезка);

Определение длины средней линии треугольника и трапеции;

Определение длины большего катета, большей диагонали;

Определение площади сложных или составных фигур;

Определение градусной меры вписанного угла.

1.Определение тангенса угла

Найдите тангенс угла А треугольника ABC, изображённого на рисунке 1.

Найдите тангенс угла AOB, изображённого
на рисунке 3.

Достроим до прямоугольного треугольника СОВ.

2. Определение площади фигуры

На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм (рис. 7). Найдите его площадь.

На клетчатой бумаге с размером клетки 1×1 изображён ромб (рис. 9). Найдите площадь этого ромба.

1. Проведем диагонали.

2. Найдем площадь

3. Определение расстояния от точки до прямой (отрезка)

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C (рис. 11). Найдите расстояние от точки A до середины отрезка BC.

Построим отрезок ВС и

отметим его середину т.О.

2. Соединим т.А с т.О. Получа-

ем нужное расстояние:

4. Определение длины средней линии треугольника и трапеции

На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC (рис. 14). Найдите длину его средней линии, параллельной стороне AC.

На клетчатой бумаге с размером клетки 1×1 изображена трапеция (рис. 15). Найдите длину её средней линии.

Основания трапеции соответствен-но равны 7 и 1

5. Определение длины большего катета, большей диагонали

На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник (рис. 16). Найдите длину его большего катета.

По рисунку видно, что длина

большего катета = 6.

6. Определение площади сложных или составных фигур

На клетчатой бумаге с размером клетки 1×1 изображена фигура (рис. 18). Найдите её площадь.

Посчитаем количество клеток внутри закрашенной области: их 19

Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке 19.

Решение: 1 способ (рис. 19.1)

Найдём площадь данной фигуры по формуле Пика:

Решение: 2 способ (рис.19.2)

Площадь данной фигуры

равна разности площади

квадрата и двух треугольников:

7. Определение градусной меры вписанного угла

Найдите угол ABC (рис. 20). Ответ дайте в градусах.

Проведём вспомогательное построение. Заметим, что дуга AC составляет ровно четверть окружности, следовательно, она равна 360°/4 = 90°.

Угол ABC — вписанный, поэтому он равен половине дуги, на которую опирается, значит, он равен половине дуги AC: 90°/2 = 45°.

Задачи для самостоятельно решения

Определение тангенса угла

Найдите тангенс угла А треугольника, изображённого на рисунке.

Найдите тангенс угла С треугольника ABC, изображённого на рисунке.

Найдите тангенс угла AOB, изображённого на рисунке.

Найдите тангенс углаAOB, изображённого на рисунке.

Найдите тангенс углаAOB, изображённого на рисунке.

Найдите тангенс угла AOB, изображённого на рисунке.

Найдите тангенс углаAOB.

Найдите тангенс углаAOB.

Найдите тангенс угла AOB.

Найдите тангенс угла, изображённого на рисунке.

Определение площади фигуры (ромба, трапеции, параллелограмма, треугольника)

На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.

На клетчатой бумаге с размером клетки 1х1 изображён треугольник. Найдите его площадь.

На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник.

На клетчатой бумаге с размером клетки 1х1 изображён ромб. Найдите его площадь.

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь.

На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь.

Определение расстояния от точки до прямой (отрезка)

На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.

На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.

На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до середины отрезка ВС. Ответ выразите в сантиметрах.

На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки А, В и С. Найдите расстояние от точки А до середины отрезка ВС. Ответ выразите в сантиметрах.

На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки А, В и С. Найдите расстояние от точки А до прямой BC. Ответ выразите в сантиметрах.

Определение длины средней линии треугольника и трапеции

На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.

На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.

На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.

На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.

На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.

На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.

Определение длины большего катета, большей диагонали

На клетчатой бумаге с размером клетки 1×1 изображен прямоугольный треугольник. Найдите длину его большего катета.

На клетчатой бумаге с размером клетки 1×1 изображен прямоугольный треугольник. Найдите длину его большего катета.

На клетчатой бумаге с размером клетки 1х1 изображён прямоугольный треугольник. Найдите длину его большего катета.

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Определение площади сложных или составных фигур

На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке.

Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке.

Определение площади сложных или составных фигур

Найдите угол ABC . Ответ дайте в градусах.

Найдите угол ABC . Ответ дайте в градусах.

Найдите угол ABC . Ответ дайте в градусах.

Найдите угол ABC . Ответ дайте в градусах.

Найдите угол ABC . Ответ дайте в градусах.

Найдите угол ABC . Ответ дайте в градусах.

I . Определение тангенса угла

II . Определение площади фигуры (ромба, трапеции, параллелограмма, треугольника

III . Определение расстояния от точки до прямой (отрезка)

IV . Определение расстояния от точки до прямой (отрезка)

V . Определение длины большего катета, большей диагонали

VI . Определение площади сложных или составных фигур

VII .Определение площади сложных или составных фигур

Открытый банк заданий ОГЭ http :// oge . fipi . ru

Выбранный для просмотра документ мастер класс.pptx

Описание презентации по отдельным слайдам:

Решение заданий №19 (задания на клетчатой бумаге) Составила учитель математики МБОУ «Виноградовская средняя школа» Безклейная Светлана Александровна

Основные типы задач Определение тангенса угла; Определение площади фигуры (ромба, трапеции, параллелограмма, треугольника); Определение расстояния от точки до прямой (отрезка); Определение длины средней линии треугольника и трапеции; Определение длины большего катета, большей диагонали; Определение площади сложных или составных фигур; Определение градусной меры вписанного угла.

При решении задач с использованием клетчатой бумаги важно помнить, что «клеточки» должны помогать! А значит, нужно подумать как они могут помочь. По «клеточкам» легко построить прямоугольный треугольник. Следовательно, могут помочь все теоретические факты связанные с прямоугольным треугольником.

Определение тангенса угла

Определение тангенса угла

Определение тангенса угла

Определение тангенса угла

Определение тангенса угла

Определение тангенса угла

Определение тангенса угла

Определение площади фигуры

Определение площади фигуры

Определение площади фигуры

Определение площади фигуры

Определение площади фигуры

Определение расстояния от точки до прямой (отрезка) Что нужно вспомнить: Расстояние от точки до пря­мой равно перпендикуляру, опу­щен­но­му из этой точки на прямую.

Определение расстояния от точки до прямой (отрезка)

Определение расстояния от точки до прямой (отрезка)

Определение расстояния от точки до прямой (отрезка)

Определение длины средней линии треугольника и трапеции Что нужно вспомнить: Средняя линия треугольника параллельна третей стороне и равна её половине; Средняя линия трапеции равна полусумме оснований.

Определение длины средней линии треугольника и трапеции

Определение длины средней линии треугольника и трапеции

Определение длины большего катета, большей диагонали Что нужно вспомнить: Стороны прямоугольного треугольника: катеты – образуют прямой угол: гипотенуза – лежит напротив прямого угла. Диагональ – отрезок соединяющий две не соседние вершины.

Задача 1 На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета. Решение: По рисунку видно, что длина большего катета = 6. Ответ: 6. Определение длины большего катета, большей диагонали

Задача 2 На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали. Решение: По рисунку видно, что длина большей диагонали = 6. Ответ: 6. Определение длины большего катета, большей диагонали

Определение площади сложных или составных фигур

Задача 1 На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь. Решение: Посчитаем ко­ли­че­ство кле­ток внут­ри за­кра­шен­ной области: их 19 Ответ: 19. Определение площади сложных или составных фигур

Определение площади сложных или составных фигур

Определение градусной меры вписанного угла Что нужно вспомнить: Вписанный угол – угол, вершина которого лежит на окружности, а стороны её пересекают. Центральный угол – угол, вершина которого совпадает с центром окружности, а стороны её пересекают. Вписанный угол равен половине дуги, на которую опирается.

Задача 1: Найдите угол ABC. Ответ дайте в градусах. Решение: Проведём вспомогательное построение. Заметим, что дуга AC составляет ровно четверть окружности, следовательно, она равна 360°/4 = 90°. Угол ABC — вписанный, поэтому он равен половине дуги, на которую опирается, значит, он равен половине дуги AC: 90°/2 = 45°. Ответ: 45. Определение градусной меры вписанного угла

Определение градусной меры вписанного угла

Определение градусной меры вписанного угла

Определение градусной меры вписанного угла

Использованы источники: Открытый банк заданий ОГЭ http://oge.fipi.ru Решу ОГЭ Математика http://oge.sdamgia.ru

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 945 человек из 79 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 678 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 305 человек из 68 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 511 310 материалов в базе

Материал подходит для УМК

«Алгебра», Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феоктистов И.Е.

Другие материалы

• 21.02.2020
• 108
• 2

• 19.02.2020
• 211
• 5

• 19.02.2020
• 172
• 1

• 19.02.2020
• 260
• 8

• 17.02.2020
• 197
• 1

• 13.02.2020
• 250
• 0

• 12.02.2020
• 491
• 1

• 12.02.2020
• 152
• 1

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 21.02.2020 28197
• RAR 4.2 мбайт
• 266 скачиваний
• Рейтинг: 5 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Безклейная Светлана Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 11 месяцев
• Подписчики: 5
• Всего просмотров: 34172
• Всего материалов: 3

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В России утвердили новые правила аккредитации образовательных учреждений

Время чтения: 1 минута

Учителя и воспитатели детсадов Подмосковья будут получать дополнительно 5 тыс. рублей

Время чтения: 1 минута

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

В Москве отмечается беспрецедентный рост заболеваемости коронавирусом среди детей

Время чтения: 2 минуты

В Петербурге открыли памятник работавшим во время блокады учителям

Время чтения: 1 минута

Большинство российских вузов используют смешанный формат обучения

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.