Нарисуйте две любые геометрические фигуры около которых можно описать окружность (4 видео)

Статья по теме «Геометрические фигуры в начальном курсе математики»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Статья по теме «Геометрические фигуры в начальном курсе математики»

По стандарту примерная образовательная программа по математике включает в себя 6 базовых содержательных линий. Среди них: «Пространственные отношения. Геометрические фигуры».

При изучении этого раздела математики за 4 года обучения учащиеся должны научиться:

— описывать взаимное расположение предметов в пространстве и на плоскости;

— распознавать, называть, представлять геометрические фигуры;

— строить геометрические фигуры с заданными измерениями (отрезок, квадрат, прямоугольник) при помощи линейки, угольника;

— применять свойства прямоугольника и квадрата при решении задач;

— различать и называть геометрические тела: куб, шар;

— сопоставлять настоящие предметы с моделями геометрических фигур;

— распознавать, различать и называть геометрические тела: параллелепипед, пирамиду, цилиндр, конус.

В начальном курсе математики изучается немалое количество геометрических фигур. Перечислю их: куб, шар, параллелепипед, пирамида, цилиндр, конус; прямой угол, многоугольник, треугольник, прямоугольник, квадрат, круг; отрезок, луч, прямая линия, ломаная линия, кривая линия (линии замкнутые, незамкнутые); точка — самая главная геометрическая фигура.

Точка – это самая малая геометрическая фигура, которая служит основой всех остальных построений (фигур) в любом изображении или чертеже; это абстрактный объект, не имеющий измерительных данных: ни длины, ни высоты, ни радиуса. Любая более сложная геометрическая фигура — это множество точек, которые обладают определенным свойством, присущим только для этой фигуры. Евклид определил точку как «объект, не имеющий частей». В нынешней аксиоматике евклидовой геометрии точка является первичным понятием, задаваемым лишь перечнем его свойств — аксиомами.

Точка обозначается цифрой или заглавной латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было отличать.

Линия — это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет. Обозначается строчными латинскими буквами.

· замкнутой, когда её начало и конец располагаются в одной точке;

· разомкнутой, когда её начало и конец не соединены.

Также имеется и такая классификация:

2. ломаная линия;

Прямая линия — это линия, которая не имеет ни начала, ни конца, путь которой равен расстоянию между двумя точками. Даже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороны.

Прямой линии присущи такие характерные особенности:

1. У прямой линии нет ни начала, ни конца, то есть она бесконечна. Есть возможность начертить только ее часть.

2. Через две любые точки можно провести прямую линию, и только одну.

3. Через произвольную точку можно провести не ограниченное количество прямых линий на плоскости.

4.Две несовпадающие прямые на плоскости либо пересекаются в одной точке, либо они параллельны.

Обозначается прямая линия при помощи одной строчной латинской буквы или же двумя заглавными латинскими буквами, обозначенными в двух разных местах этой прямой.

Прямые могут быть:

— пересекающимися, если имеют общую точку. Две прямые могут пересекаться только в одной точке;

— перпендикулярными, если пересекаются под прямым углом (90°);

— параллельными, если не пересекаются, не имеют общей точки.

Ломаная линия — это некоторое количество отрезков, соединенных друг с другом так, что конец первого отрезка является началом второго отрезка, а конец второго отрезка — началом третьего отрезка и т. д., при этом соседние (имеющие одну общую точку) отрезки расположены не на одной прямой. Если конец последнего отрезка не совпадает с началом первого, то такая ломаная линия называется незамкнутой. Если конец последнего отрезка ломаной совпадает с началом первого отрезка, то такая ломаная линия называется замкнутой.

Луч — это направленная полупрямая, которая имеет точку начала и не имеет конца.

Если на прямой поставить точку, то этой точкой прямая разбивается на два луча, противоположно направленных. Такие лучи называются дополнительными.

Луч обозначается строчной латинской буквой или двумя заглавными латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче .

Лучи совпадают, если:

— расположены на одной и той же прямой,

— начинаются в одной точке,

— направлены в одну сторону.

Отрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину. Длина отрезка — это расстояние между его начальной и конечной точками.

Отрезок обозначается двумя заглавными латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, которой заканчивается отрезок.

Квадрат — четырехугольник, у которого все стороны равны, а все углы прямые. Квадраты отличаются только длиной стороны, а все 4 угла прямые и равны 90°. Квадратом может стать параллелограмм, ромб или прямоугольник, когда у них одинаковые длины диагоналей, сторон и равные углы.

Выделим основные свойства квадрата:

— у всех четырех сторон квадрата одинаковая длина, т.е. стороны квадрата равны: AB = BC = CD = AD

— противолежащие стороны квадрата параллельны: AB||CD, BC||AD

— каждый угол квадрата прямой: ∠ ABC = ∠ BCD = ∠ CDA = ∠ DAB = 90°

— сумма углов квадрата равна 360°: ∠ ABC + ∠ BCD + ∠ CDA + ∠ DAB = 360°

— каждая диагональ квадрата имеет такую же длину, как и другая:

— каждая диагональ делит его на 2 одинаковые симметричные фигуры;

— угол пересечения диагоналей квадрата равен 90°, пересекая друг друга, диагонали делятся на две равные части:

AC┴BD;AO = BO = CO = DO = d/2

— точку пересечения диагоналей называют центром квадрата, и она оказывается центром вписанной и описанной окружностей.

— все диагонали делят угол квадрата на две равные части, таким образом, они оказываются биссектрисами углов квадрата:

ΔABC = ΔADC = ΔBAD = ΔBCD

∠ ACB = ∠ ACD = ∠ BDC = ∠ BDA = ∠ CAB = ∠ CAD = ∠ DBC = ∠ DBA = 45°

— диагонали делят квадрат на 4 одинаковых треугольника, кроме того, полученные треугольники в одно время и равнобедренные и прямоугольные:

ΔAOB = ΔBOC = ΔCOD = ΔDOA

Круг – геометрическая фигура, состоящая из всех точек плоскости, находящихся внутри окружности.

Прямоугольник — это четырехугольник, у которого все углы прямые. Квадрат — это частный случай прямоугольника.

У прямоугольника есть две пары равных сторон. Длина более длинных пар сторон называется длиной прямоугольника, а длина более коротких — шириной прямоугольника.

К основным свойствам прямоугольника можно отнести следующие:

1. Прямоугольник – это параллелограмм;

2. Противоположные стороны равны: AB = CD , BC = AD ;

3. Противоположные стороны параллельны: AB ∥ CD , BC ∥ AD ;

4. Прилегающие стороны перпендикулярны друг другу: AB ⊥ BC , BC ⊥ CD , CD ⊥ AD , AD ⊥ AB ;

5. Диагонали прямоугольника равны: AC=BD;

6. Квадрат диагонали равен сумме квадратов двух прилежащих его сторон. Это свойство справедливо в силу теоремы Пифагора: AC 2 =AD 2 +CD 2;

7. Диагональ делит прямоугольник на два одинаковых прямоугольных треугольника: BCD △ ABC = △ ACD , △ ABD = △ BCD ;

8. Точка пересечения диагоналей является центром прямоугольника и описанной окружности;

9. Сумма всех углов равна 360 градусов: ∠ ABC + ∠ BCD + ∠ CDA + ∠ DAB =360

Треугольник — это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки.

В любом треугольнике имеется три угла и три стороны. Сумма углов любого треугольника равна 180 о . Против большего угла треугольника лежит большая сторона.

— остроугольные (когда все его углы острые),

— тупоугольные (когда один из его углов тупой),

— прямоугольные (когда один из его углов прямой).

— равнобедренным, если две его стороны равны.

— равносторонним, если все три стороны равны,

— разносторонним, если все его стороны разные.

Основные линии треугольника:

· Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

· Биссектрисой угла треугольника называется луч, исходящий из вершины треугольника и делящий его пополам.

· Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на противоположную сторону (или ее продолжение).

· Средняя линия треугольника – это отрезок, соединяющий середины двух сторон треугольника и параллельный третьей стороне.

· В любой треугольник можно вписать окружность и около любого треугольника можно описать окружность.

· Два треугольника называются равными, если у них равны соответствующие стороны и соответствующие углы.

Многоугольник — это геометрическая фигура, ограниченная со всех сторон замкнутой ломаной линией, состоящая из трех и более отрезков (звеньев).

Многоугольники характеризуются углами, которые составляет каждая пара отрезков замкнутой ломаной, имеющих одну общую точку, и количеством отрезков ломаной линии. Количество отрезков замкнутой ломаной линии и количество углов в каждом многоугольнике совпадают. Если замкнутая ломаная линия состоит из трех отрезков, то такой многоугольник называется треугольником, из четырех отрезком — четырехугольником, из пяти отрезков — пятиугольником и т. д.

Конус – тело, состоящее из круга – основание конуса, точки, не принадлежащей плоскости этого круга, – вершины конуса и всех отрезков, соединяющих вершину конуса и точки окружности основания. Отрезки, которые соединяют вершину конуса с точками окружности основания, называются образующими конуса. Поверхность конуса состоит из основания и боковой поверхности.

Пирамида — многогранник, в основании которого лежит многоугольник, а остальные грани являются треугольниками, которые имеют общую вершину. Пирамида – это частный случай конуса.

1. апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины;

2. боковые грани — треугольники, которые сходятся в вершине;

3. боковые ребра — общие стороны боковых граней;

4. вершина пирамиды — точка, соединяющая боковые ребра и не лежащая в плоскости основания;

5. высота — отрезок перпендикуляра, который проведен через вершину пирамиды к плоскости ее основания;

6. диагональное сечение пирамиды — сечение пирамиды, которое проходит через вершину и диагональ основания;

7. основание (ABCD) — многоугольник, которому не принадлежит вершина пирамиды.

Цилиндр – тело, состоящее из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей кругов, – образующими цилиндра.

Площадь боковой поверхности цилиндра высчитывается через высоту и радиус: S=2πrh, где π — константа равная (3.14); r — радиус основания; h — высота цилиндра.

Шар – это тело, состоящее из всех точек пространства, которые находятся на расстоянии, не большем данного от исходной точки. Эта точка называется центром шара, а данное расстояние – радиусом шара. Граница шара называется шаровой поверхностью или сферой. Точками сферы являются все точки шара, которые удалены от центра на расстояние, равное радиусу. Проходящий через центр шара отрезок, который соединяет две точки шаровой поверхности, называется диаметром.

Площадь поверхности шара можно найти по формулам:

S = 4 πr2 или S = πd2, где r – радиус шара, d – диаметр шара.

Объём шара находится по формуле: V = 4 / 3 πr3, где r – радиус шара.

Итак, ознакомившись с некоторыми геометрическими фигурами, можно сказать, что младшим школьникам будет полезно знать о конкретных фигурах, их свойствах; к тому же все эти знания пригодятся в повседневной жизни.

Содержание

Плоские геометрические фигуры: свойства и основные формулы
Четырёхугольник
Основные свойства:
Квадрат
Основные формулы:
Свойства:
Прямоугольник
Основные формулы:
Свойства:
Параллелограмм
Определения:
Основные формулы:
Свойства:
Ромб
Основные формулы:
Свойства:
Трапеция
Определения:
Основные формулы:
Свойства:
Треугольник
Определения:
Основные формулы:
Свойства:
Окружность
Определения:
Основные формулы:
Описанная окружность
Доказательство
Доказательство
Доказательство
Доказательство
Доказательство
🎦 Видео

Видео:Здравствуйте. Тема «Геометрические фигуры» от 22.12.20 натюрморт, карандашСкачать

Плоские геометрические фигуры: свойства и основные формулы

В статье описываются геометрические фигуры: определение, основные свойства и формулы.

Плоские геометрические фигуры:

Четырехугольник (общее для всех четырехугольников)

Квадрат

Прямоугольник

Параллелограмм

Трапеция

Треугольник

Окружность

Геометрические фигуры — это любое сочетание точек, линий и поверхностей. Геометрические фигуры разделяются на плоские и объемные.

Плоские геометрические фигуры — это фигуры, все точки которых лежат на одной плоскости. Объемные геометрические фигуры — это фигуры, не все точки которых лежат на одной плоскости.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Четырёхугольник

Четырёхугольник – это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три точки не лежат на одной прямой.

Основные свойства:

Сумма углов четырёхугольника равна 360°
Не существует четырёхугольников, у которых все углы острые или все углы тупые.
Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов.
Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон.

В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны. Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.

Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°.Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.

Видео:Натюрморт из геометрических предметовСкачать

Квадрат

Квадрат – правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.

Основные формулы:

Периметр: P=4a, где P-периметр, a-сторона
Площадь: S=a 2 или S=d 2 /2
Сторона и диагональ связаны соотношениями: a=d/√2, d=a√2
Радиус описанной окружности: R=d или R=a/√(2)
Радиус вписанной окружности: r=a/2

где a-сторона, d-диагональ, P-периметр, S-площадь
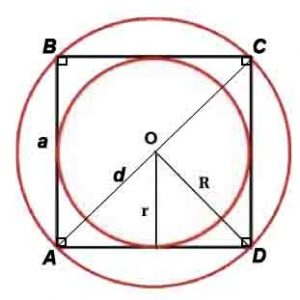
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(2) – корень квадратный из 2.

Свойства:

Все стороны равны, все углы равны и составляют 90°;
Диагонали квадрата равны и перпендикулярны;
У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей;
Квадрат является одновременно частным случаем ромба и прямоугольника.

Видео:Построить описанную окружность (Задача 1)Скачать

Прямоугольник

Прямоугольник – четырехугольник, у которого все углы прямые.

Основные формулы:

Периметр: P=(a+b)*2
Площадь по сторонам: S = a*b
Площадь по диагонали и углу между ними: S = d²* sin γ. / 2
Стороны и диагональ связаны соотношением: d=√(a 2 +b 2 )/2 (теорема Пифагора)
Радиус описанной окружности: R= √(a 2 +b 2 )/2 (теорема Пифагора)

где a, b – длины сторон прямоугольника, d-диагональ, P-периметр, S-площадь
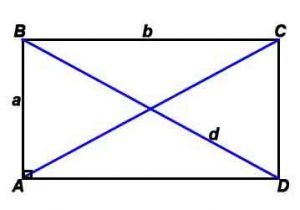
γ – угол между диагоналями
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(a 2 +b 2 ) – корень квадратный из (a 2 +b 2 ).

Свойства:

Диагонали прямоугольника равны и делятся точкой пересечения пополам.
Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали.

Видео:КАК НАРИСОВАТЬ КРУГ В ИЗОМЕТРИИ (ОВАЛ В ИЗОМЕТРИЧЕСКОЙ ПРОЕКЦИИ).Скачать

Параллелограмм

Параллелограмм – четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.

Определения:

Высота параллелограмма – это перпендикуляр, проведённый из вершины параллелограмма к противоположной стороне.

Основные формулы:

Стороны и диагональ связаны соотношением: (d₁) 2 +(d₂) 2 =(a 2 +b 2 )*2
Периметр: P=(a+b)*2
Площадь по стороне и высоте: S = a*h
S (Площадь) по двум сторонам и углу между ними: S=a*b*sin α
S (Площадь) по двум диагоналям и углу между ними: S=(d₁*d₂)/2*sin γ

где a, b – длины сторон, d₁, d₂ –диагонали, P-периметр, S-площадь,
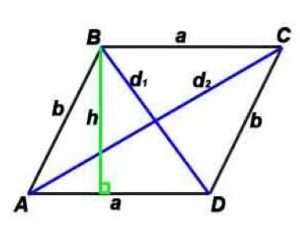
h-высота, проведенная к противоположной стороне
α – угол между сторонами параллелограмма,
γ – угол между диагоналями параллелограмма (острый).

Свойства:

У параллелограмма противоположные стороны равны и противоположные углы равны.
Сумма любых двух соседних углов параллелограмма равна 180°.
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
Каждая диагональ делит параллелограмм на два равных треугольника.
Две диагонали параллелограмма делят его на четыре равновеликих треугольника (равны площади всех 4-х треугольников)
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Ромб

Ромб – это параллелограмм, у которого все стороны равны.

Основные формулы:

Периметр: P=4*a
Площадь по стороне и высоте: S=a*h
Площадь по диагоналям: S = (d₁*d₂)/2
Радиус окружности, вписанной в ромб: r=h/2 или r =(d₁*d₂)/4a
Площадь по стороне и радиусу вписанной окружности: S=2*a*r
Площадь по стороне и углу: S = a 2 · sin α

где a – длина стороны, d₁, d₂ –диагонали, P-периметр, S-площадь,
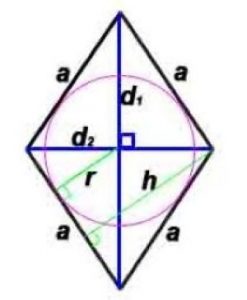
h -высота, проведенная к противоположной стороне
α – угол между сторонами ромба

Свойства:

Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.
В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей. Радиус окружности: r=h/2 или r = d₁*d₂/4a.

Видео:1 2 4 сопряжение окружностейСкачать

Трапеция

Трапеция – четырёхугольник, у которого только две противолежащие стороны параллельны.

Определения:

Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.
Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.
Средняя линия (первая средняя линия) трапеции – отрезок, который соединяет середины боковых сторон данной трапеции.Средняя линия трапеции параллельна её основаниям и равна их полусумме.
Средняя линия (вторая средняя линия) – отрезок, соединяющий середины оснований, проходит через точку пересечения диагоналей.
Равнобокая трапеция – трапеция,у которой боковые стороны равны (c=d). У равнобокой трапеции:диагонали равны, углы при основании равны, сумма противолежащих углов равна 180°.Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая.
Прямоугольная трапеция – трапеция, у которой одна из её боковых сторон перпендикулярна основаниям.

Основные формулы:

Периметр: P=a+b+c+d
Площадь определить: S=h*(a+b)/2
Стороны и диагональ равнобокой трапеции: d² = ab+c²
Радиус вписанной окружности: r = h/2

где a,b – основания, c,d – боковые стороны (с – боковые стороны в случае, если трапеция равнобокая), d₁, d₂ –диагонали,
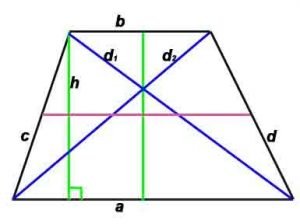
P-периметр, S-площадь, h -высота, проведенная к противоположной стороне

Свойства:

В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон (a+b=c+d). Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Треугольник

Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).

Определения:

Углами (внутренними углами) треугольника называются три угла, каждый из которых образован лучами, выходящими из вершин треугольника и проходящими через две другие вершины.
Высота треугольника – перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны
Медиана треугольника– отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне
Равные треугольники – треугольники, у которых соответствующие стороны равны и соответствующие углы равны
Равнобедренный треугольник– треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
Равносторонний или правильный треугольник – треугольник, у которого все стороны равны.
Прямоугольный треугольник – треугольник, у которого есть прямой угол. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.

Основные формулы:

Периметр: P=a+b+c
Площадь по стороне и высоте: S=(a*h)/2
Площадь: по сторонам и углу между ними: S=(a*b)/2* sin γ
по трем сторонам и радиусу описанной окружности: S=(a*b*c)/4R
по трем сторонам и радиусу вписанной окружности: S=(a+b+c)/2*r
Площадь прямоугольного треугольника: S=(a*b)/2
Стороны прямоугольного треугольника: c 2 =a 2 +b 2 (Теорема Пифагора)

где a,b, c – стороны (a,b –катеты , с – гипотенуза в случае прямоугольного треугольника)
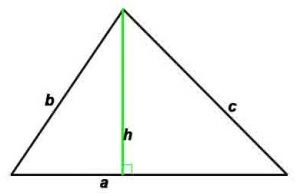
d₁, d₂ –диагонали, h -высота, проведенная к противоположной стороне,
P-периметр, S-площадь, γ – угол между сторонами a и b
r – радиус вписанной окружности, R – радиус описанной окружности

Свойства:

В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.
Сумма углов треугольника равна 180°:
Длина каждой стороны треугольника больше разности и меньше суммы длин двух других сторон: |a-b| 2 =a 2 +b 2 (Теорема Пифагора).В прямоугольном треугольнике гипотенуза всегда больше любого из катетов.

Видео:Урок №7. Рисунок | Рисунок 3-х геометрических тел, контрастных по форме и тону на светлом фонеСкачать

Окружность

Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра окружности), которая лежит в той же плоскости, что и кривая.

Определения:

Радиус – отрезок, который соединяет центр окружности с любой её точкой.
Хорда – отрезок, который соединяет какие-либо две точки окружности (AB).
Диаметр – хорда, проходящая через центр окружности(d). Диаметр – наибольшая хорда окружности. Наименьшей хорды окружности не существует.
Касательная – прямая, которая лежит в одной плоскости с окружностью и имеет с ней только одну общую точку (E)
Секущая – прямая, которая пересекает окружность в двух различных точках.

Основные формулы:

Длина окружности: L = 2πR
Площадь круга: S = π*r 2 или S = π*d 2 /4

где π = 3,14 (3,1415926535) – величина постоянная,
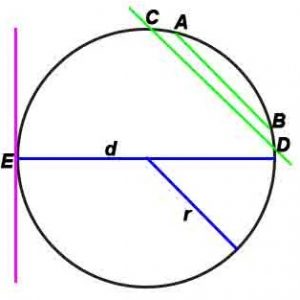
где r-радиус, d –диаметр, L – длина окружности, S-площадь.

Видео:ТЕМА 2. ПОСТРОЕНИЕ КУБА, ЦИЛИНДРА, ШАРАСкачать

Описанная окружность

Окружность описанная около многоугольника — это окружность, на которой лежат все вершины многоугольника. Вписанный в окружность многоугольник — это многоугольник, все вершины которого лежат на окружности. На рисунке 1 четырехугольник АВСD вписан в окружность с центром О, а четырехугольник АЕСD не является вписанным в эту окружность, так как вершина Е не лежит на окружности.

Теорема

Около любого треугольника можно описать окружность.

Доказательство

Дано: произвольный АВС.

Доказать: около АВС можно описать окружность.

Доказательство:

1. Проведем серединные перпендикуляры к сторонам АВС, которые пересекутся в точке О (по свойству серединных перпендикуляров треугольника). Соединим точку О с точками А, В и С (Рис. 2).

Точка О равноудалена от вершин АВС (по теореме о серединном перпендикуляре), поэтому ОА = ОВ = ОС. Следовательно, окружность с центром О радиуса ОА проходит через все три вершины треугольника, значит, является описанной около АВС. Теорема доказана.

Замечание 1

Около треугольника можно описать только одну окружность.

Доказательство

Предположим, что около треугольника можно описать две окружности. Тогда центр каждой из них равноудален от его вершин и поэтому совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки О до вершин треугольника. Следовательно, эти окружности совпадают, т.е. около треугольника можно описать только одну окружность. Что и требовалось доказать.

Замечание 2

Около четырехугольника не всегда можно описать окружность.

Доказательство

Рассмотрим, например, ромб, не являющийся квадратом. Такой ромб можно «поместить» в окружность так, что две его вершины будут лежать на этой окружности (Рис. 3), но нельзя «поместить» ромб в окружность так, чтобы все его вершины лежали на окружности, т.к. диаметр окружности, равный одной из диагоналей ромба, будет больше (меньше) второй диагонали, т.е. нельзя описать окружность. Что и требовалось доказать.

Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:

В любом вписанном четырехугольнике сумма противоположных углов равна 180 0 .

Доказательство

Рассмотрим четырехугольник АВСD, вписанный в окружность (Рис. 4).

Углы В и D — вписанные, тогда по теореме о вписанном угле: В = АDС, D = АВС, откуда следует В + D = АDС + АВС = (АDС + АВС). Дуги АDС и АВС вместе составляют окружность, градусная мера которой равна 360 0 , т.е. АDС + АВС = 360 0 , тогда В + D = 360 0 = 180 0 . Что и требовалось доказать.

Верно и обратное утверждение:

Если сумма противоположных углов четырехугольника равна 180 0 , то около него можно описать окружность.

Доказательство

Дано: четырехугольник АВСD, BАD + BСD = 180 0 .

Доказать: около АВСD можно описать окружность.

Доказательство:

Проведем окружность через три вершины четырехугольника: А, В и D (Рис. 5), — и докажем, что она проходит также через вершину С, т.е. является описанной около четырехугольника АВСD.

Предположим, что это не так. Тогда вершина С лежит либо внутри круга, либо вне его.

Рассмотрим первый случай, когда точка С лежит внутри круга (Рис. 6).

ВСD — внешний угол СFD, следовательно, BСD = ВFD + FDE. (1)

Углы ВFD и FDE — вписанные. По теореме о вписанном угле ВFD = ВАD и FDE = ЕF, тогда, подставляя данные равенства в (1), получим: BСD = ВАD + ЕF = (ВАD + ЕF), следовательно, ВСDВАD.

BАD — вписанный, тогда по теореме о вписанном угле BАD = ВЕD, тогда BАD + BСD(ВЕD + ВАD).

Дуги ВЕD и ВАD вместе составляют окружность, градусная мера которой равна 360 0 , т.е. ВЕD + ВАD = 360 0 , тогда BАD + BСD360 0 = 180 0 .

Итак, мы получили, что BАD + BСD180 0 . Но это противоречит условию BАD + BСD =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность.

Рассмотрим второй случай, когда точка С лежит вне круга (Рис. 7).

По теореме о сумме углов треугольника в ВСF: С + В + F = 180 0 , откуда С = 180 0 — ( В + F). (2)

В — вписанный, тогда по теореме о вписанном угле В = ЕF. (3)

F и ВFD — смежные, поэтому F + ВFD = 180 0 , откуда F = 180 0 — ВFD = 180 0 — ВАD. (4)

Подставим (3) и (4) в (2), получим:

С = 180 0 — (ЕF + 180 0 — ВАD) = 180 0 — ЕF — 180 0 + ВАD = (ВАD — ЕF), следовательно, СВАD.

А — вписанный, тогда по теореме о вписанном угле А = ВЕD, тогда А + С(ВЕD + ВАD). Но это противоречит условию А + С =180 0 , и, значит, наше предположение ошибочно, т.е. точка С лежит на окружности, значит, около четырехугольника АВСD можно описать окружность. Что и требовалось доказать.