Плоскость, проходящая через данную точку М0(х0;у0;z0) и параллельная данным прямым K1 и K2 (при этом прямые K1 и K2 не параллельным между собой), выражается уравнением:
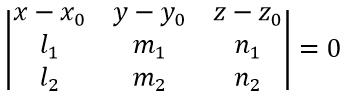
где l 1, m1, n1, l 2, m2, n2 — направляющие коэффициенты данных прямых.
Запись в векторной форме:
Примечание
Если данные прямые K1 и K2 параллельны между собой, то уравнение (1) имеет бесчисленное множество решений (получаем пучок плоскостей с осью, проходящей через точку М0 и параллельно данным прямым).
- Уравнение плоскости, проходящей через данную прямую параллельно другой прямой онлайн
- Предупреждение
- Уравнение плоскости, проходящей через данную прямую параллельно другой прямой − теория, примеры и решения
- Математический портал
- Nav view search
- Navigation
- Search
- Расстояние между двумя скрещивающимися прямыми.
- 📸 Видео
Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Уравнение плоскости, проходящей через данную прямую параллельно другой прямой онлайн
С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через прямую L1 параллельно другой прямой L2 (прямые L1 и L2 не параллельны). Дается подробное решение с пояснениями. Для построения уравнения плоскости задайте вид уравнения прямых (канонический или параметрический) введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Уравнение плоскости, проходящей через данную прямую параллельно другой прямой − теория, примеры и решения
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2, которые не параллельны:
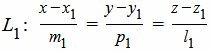 . . | (1) |
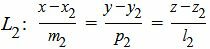 . . | (2) |
Задача заключается в построении уравнения плоскости α, проходящей через прямую L1 параллельно прямой L2(Рис.1).
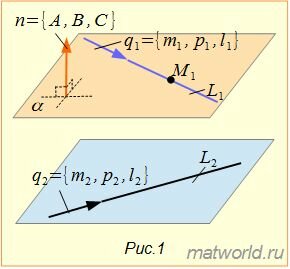 |
Прамая L1 должна лежать на искомой плоскости α, следовательно точка M1 должна нежать на плоскости α.
Уравнение плоскости можно записать формулой
| Ax+By+Cz+D=0. | (3) |
и поскольку M1(x1, y1, z1) принадлежит этой плоскости, то справедливо следующее равенство:
| Ax1+By1+Cz1+D=0. | (4) |
Для того, чтобы плоскость α проходила через прямую L1, нормальный вектор плоскости n=<A, B, C> должен быть ортогональным направляющему вектору q1 прямой L1, т.е. скалярное произведение этих векторов должен быть равным нулю:
| Am1+Bp1+Cl1=0 | (5) |
Для того, чтобы плоскость α была параллельна прямой L2, нормальный вектор плоскости n=<A, B, C> должен быть ортогональным направляющему вектору q2 прямой L2, т.е. скалярное произведение этих векторов должен быть равным нулю:
| Am2+Bp2+Cl2=0 | (6) |
Таким образом мы должны решить систему трех уравнений с четыремя неизвестными (4)−(6). Представим систему линейных уравнений (4)−(6) в матричном виде:
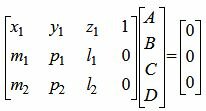 | (7) |
Решив однородную систему линейных уравнений (7) найдем частное решение. (как решить систему линейных уравнений посмотрите на странице метод Гаусса онлайн). Подставляя полученные коэффициенты A, B, C и D в уравнение (3), получим уравнение плоскости, проходящей через прямую L1 параллельно прямой L2.
Пример 1. Найти уравнение плоскости α, проходящей через прямую L1:
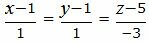 | (8) |
паралленьно другой прямой L2 :
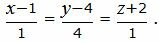 | (9) |
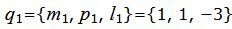 |
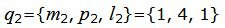 |
Поскольку плоскость проходит через прямую L1 , то она проходит также через точку M1(x1, y1, z1)=M1(1, 1, 5) и нормальный вектор плоскости n=<A, B, C> перпендикулярна направляющему вектору q1=<m1, p1, l1>= прямой L1. Тогда уравнение плоскости должна удовлетворять условию:
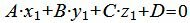 | (10) |
а условие параллельности прямой L1 и искомой плоскости α представляется следующим равенством:
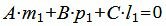 | (11) |
Так как плоскость α должна быть параллельной прямой L2, то должна выполнятся условие:
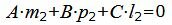 | (12) |
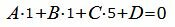 | (13) |
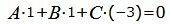 | (14) |
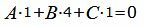 | (15) |
Представим эти уравнения в матричном виде:
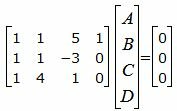 | (16) |
Решим систему линейных уравнений (16) отностительно A, B, C, D:
 | (17) |
Так как искомая плоскость проходит через точку M1 и имеет нормальный вектор n=<A, B, C>= то она может быть представлена формулой:
| Ax+By+Cz+D=0 | (18) |
Подставляя значения A,B,C,D в (17), получим:
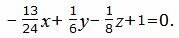 | (18) |
Уравнение плоскости можно представить более упрощенном виде, умножив на число −24:
| 13x−4y+3z−24=0 | (19) |
Ответ: Уравнение плоскости, проходящей через прямую (1) параллельно прямой (2) имеет вид (19).
Пример 2. Найти уравнение плоскости α, проходящей через прямую L1:
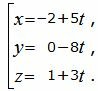 | (20) |
| q1=<m1, p1, l1>= |
| q2=<m2, p2, l2>= |
Поскольку плоскость проходит через прямую L1 , то она проходит также через точку M1(x1, y1, z1)=M1(−2, 0, 1) и нормальный вектор плоскости n=<A, B, C> перпендикулярна направляющему вектору q1=<m1, p1, l1>= прямой L1. Тогда уравнение плоскости должна удовлетворять условию:
| Ax1+By1+Cz1+D=0 | (22) |
а условие параллельности прямой L1 и искомой плоскости α представляется следующим равенством:
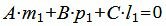 | (23) |
Так как плоскость α должна быть параллельной прямой L2, то должна выполнятся условие:
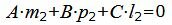 | (24) |
| A(−2)+B·0+C·1+D=0, | (25) |
| A·5+B(−8)+C·3=0, | (26) |
| A·1+B·1+C·1=0, | (27) |
Представим эти уравнения в матричном виде:
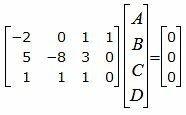 | (28) |
Решим систему линейных уравнений (28) отностительно A, B, C, D:
 | (29) |
Так как искомая плоскость проходит через точку M1 и имеет нормальный вектор n=<A, B, C>= то она может быть представлена формулой:
| Ax+By+Cz+D=0 | (30) |
Подставляя значения A,B,C,D в (30), получим:
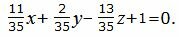 | (31) |
Уравнение плоскости можно представить более упрощенном виде, умножив на число 35:
| 11x+2y−13z+35=0 | (32) |
Ответ: Уравнение плоскости, проходящей через прямую (1) параллельно прямой (2) имеет вид (32).
Видео:Уравнение плоскости через 2 точки параллельно векторуСкачать

Математический портал
Видео:Уравнение плоскости через 2 точки параллельно прямойСкачать

Nav view search
Navigation
Search
- Вы здесь:
- Home
Видео:10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Расстояние между двумя скрещивающимися прямыми.
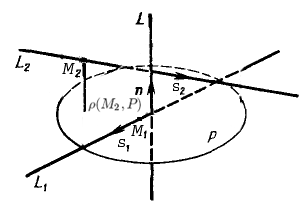
Пусть $L_1: frac=frac=frac$ и $L_2: frac=frac=frac$ — две скрещивающиеся прямые. Расстояние $rho(L_1, L_2)$ между прямыми $L_1$ и $L_2$ можно найти по следующей схеме:
1) Находим уравнение плоскости $P,$ проходящей через прямую $L_1,$ параллельно прямой $L_2:$
Плоскость $P$ проходит через точку $M_1(x_1, y_1, z_1),$ перпендикулярно вектору $overline n=[overline s_1, overline s_2]=(n_x, n_y, n_z),$ где $overline s_1=(m_1, l_1, k_1)$ и $overline s_2=(m_2, l_2, k_2)$ — направляющие вектора прямых $L_1$ и $L_2.$ Следовательно, уравнение плоскости $P: n_x(x-x_1)+n_y(y-y_1)+n_z(z-z_1)=0.$
2) Расстояние между прямыми $L_1$ и $L_2$ равно расстоянию от любой точки прямой $L_2$ до плоскости $P:$
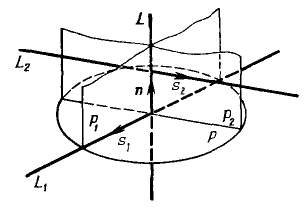
Нахождение общего перпендикуляра скрещивающихся прямых.
Для нахождения общего перпендикуляра прямых $L_1$ и $L_2,$ необходимо найти уравнения
плоскостей $P_1$ и $P_2,$ проходящих, соответственно, через прямые $L_1$ и $L_2,$ перпендикулярно плоскости $P.$
Пусть $P_1: A_1x+B_1y+C_1z+D_1=0;$
Тогда уравнение общего перпендикуляра имеет вид
Пример.
2.214.
а) доказать, что прямые не лежат в одной плоскости, то есть являются скрещивающимися;
б) написать уравнение плоскости, проходящей через прямую $L_2$ параллельно $L_1;$
в) вычислить расстояние между прямыми;
г) написать уравнения общего перпендикуляра к прямым $L_1$ и $L_2.$
Решение.
а) Если прямые $L_1$ и $L_2$ лежат в одной плоскости, то их направляющие вектора $overline(3, 4, -2),$ $overline(6, -4, -1),$ и вектор $overline l,$ соединяющий произвольную точку прямой $L_1$ и произвольную точку прямой $L_2$ компланарны. В качестве такого вектора $overline$ можно выбрать $overline(x_2-x_1, y_2-y_1, z_2-z_1).$ Проверим будут ли эти вектора компланарны.
Следовательно, вектора не компланарны и прямые не лежат в одной плоскости.
б) Запишем уравнение плоскости, проходящей через прямую $L_2$ параллельно $L_1.$ Эта плоскость проходит через точку $M_2(21, -5, 2)$ перпендикулярно вектору $overline n=[overline s_1, overline s_2].$
Таким образом, вектор $overline n$ имеет координаты $overline n(-12, -9, -36).$
Находим уравнение плоскости $$P:,, -12(x-21)-9(y+5)-36(z-2)=0Rightarrow$$ $$Rightarrow-12x-9y-36z+252-45+72=0Rightarrow -12x-9y-36z+279=0Rightarrow$$ $$Rightarrow 4x+3y+12z-93=0.$$
в) Расстояние между прямыми $L_1$ и $L_2$ равно расстоянию от любой точки прямой $L_1$ до плоскости $P:$
Ответ: $frac.$
г) Найдем уравнения плоскостей $P_1$ и $P_2,$ проходящих, соответственно, через прямые $L_1$ и $L_2,$ перпендикулярно плоскости $P.$
Имеем, $M_1=(-7, -4, -3)in P_1,$
Таким образом, $$P_1: 54(x+7)-44(y+4)-7(z+3)=54x-44y-7z+378-176-21=$$ $$=54x-44y-7z+181=0.$$
Аналогично находим $P_2:$
Имеем, $M_2=(21, -5, 2)in P_2,$
Таким образом, $$P_1: -45(x-21)-76(y+5)+34(z-2)=-45x-76y+34z+945-380-68=$$ $$=-45x-76y+34z+497=0.$$
Ответ: $left<begin54x-44y-7z+181=0;\ -45x-76y+34z+497=0.endright. $
2.215.
а) доказать, что прямые не лежат в одной плоскости, то есть являются скрещивающимися;
б) написать уравнение плоскости, проходящей через прямую $L_2$ параллельно $L_1;$
в) вычислить расстояние между прямыми;
г) написать уравнения общего перпендикуляра к прямым $L_1$ и $L_2.$
Ответ: б) $4x+12y+12z+76=0;$
г) $left<begin53x-7y-44z-429=0;\ 105x-23y-48z+136=0.endright. $
📸 Видео
Задача 8. Написать уравнение плоскости, проходящей через точку перпендикулярно вектору.Скачать

2. Уравнение плоскости примеры решения задач #1Скачать

Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

12. Уравнения прямой в пространстве Решение задачСкачать

3. Частные случаи общего уравнения плоскости Неполные уравнения плоскостиСкачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Найти уравнение плоскости проходящей через прямую и перпендикулярно плоскостиСкачать

Видеоурок "Уравнение плоскости по трем точкам"Скачать

Написать канонические и параметрические уравнения прямой в пространствеСкачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать