Представлена самостоятельная работа в двух вариантах по геометрии для учащихся 10 класса на тему «Взаимное расположение прямых в пространстве. Скрещивающиеся прямые».
- Просмотр содержимого документа «Самостоятельная работа по теме «Взаимное расположение прямых в пространстве. Скрещивающиеся прямые».»
- Практическая работа №5 по теме «Параллельность прямых и плоскостей» для студентов 1 курса
- «Календарь счастливой жизни: инструменты и механизм работы для достижения своих целей»
- 5.2.1 Пересекающиеся, параллельные и скрещивающиеся прямые; перпендикулярность прямых
- 🔥 Видео
Просмотр содержимого документа
«Самостоятельная работа по теме «Взаимное расположение прямых в пространстве. Скрещивающиеся прямые».»
Взаимное расположение прямых в пространстве. Скрещивающиеся прямые.
1.Сформулировать определение скрещивающихся прямых
а) пересекающихся прямых б) параллельных прямых в) скрещивающихся прямых.
3 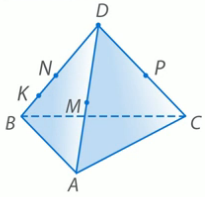
4. Точка D не лежит в плоскости треугольника АВС, точки M, N, P – середины отрезков DA, DB и DC соответственно, точка K лежит на отрезке BN . Выясните взаимное расположение прямых. 1) ND и AB
1. Перечислить все возможные случаи расположения двух прямых в пространстве
2. Начертите прямоугольный параллелепипед MKСDM 1K1C 1D1. Запишите по две пары: а) пересекающихся прямых б) параллельных прямых в) скрещивающихся прямых.
3. Прямая МА проходит через вершину квадрата АВСD и не лежит в плоскости квадрата. Докажите, что МА и ВС скрещивающиеся .
4 
Взаимное расположение прямых в пространстве. Скрещивающиеся прямые.
1.Сформулировать определение скрещивающихся прямых
а) пересекающихся прямых б) параллельных прямых в) скрещивающихся прямых.
3 
4. Точка D не лежит в плоскости треугольника АВС, точки M, N, P – середины отрезков DA, DB и DC соответственно, точка K лежит на отрезке BN . Выясните взаимное расположение прямых. 1) ND и AB
1. Перечислить все возможные случаи расположения двух прямых в пространстве
2. Начертите прямоугольный параллелепипед MKСDM 1K1C 1D1. Запишите по две пары: а) пересекающихся прямых б) параллельных прямых в) скрещивающихся прямых.
3. Прямая МА проходит через вершину квадрата АВСD и не лежит в плоскости квадрата. Докажите, что МА и ВС скрещивающиеся .
4 
Видео:Перпендикулярные прямыеСкачать

Практическая работа №5 по теме «Параллельность прямых и плоскостей» для студентов 1 курса
Видео:10 класс, 7 урок, Скрещивающиеся прямыеСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»
Сертификат и скидка на обучение каждому участнику


Тема: «Параллельность прямых и плоскостей».
— формирование логического мышления, пространственного воображения через решение задач;
— развить умение составлять наглядные рисунки для задач;
— воспитывать самостоятельные навыки.
1. Ответить на контрольные вопросы:
1). Записать признак параллельности прямой и плоскости (с рисунком).
2). Записать признак скрещивающихся прямых (с рисунком).
3). Записать признак параллельности плоскостей (с рисунком).
2. Выполнить контрольное задание.
Образец выполнения заданий.
1) параллельные прямые к АВ; 2) скрещивающиеся прямые к ВС.
Решение:
2. Точка М лежит на середине ребра AD тетраэдра DABC . Построить сечение тетраэдра плоскостью, проходящей через точку М параллельно основанию АВС.
Решение:
Т.к. секущая плоскость проходит параллельно основанию => отрезки параллельных плоскостей будут параллельны по свойству параллельности плоскостей ( 1°. Если 2-е параллельные плоскости пересечены третьей, то линии их пересечения будут параллельны).
1. Построим через т. М, MN ǁАВ.
2. Построим через т. N , NK ǁВС.
3. Соединим МК по 2*.
4. MNK — искомое сечение.
3. Средняя линия трапеции лежит в плоскости α. Докажите, что основания трапеции параллельны плоскости α.
MN — средняя линия трапеции, MN ⊂ α.
Доказать: ВСǁα, AD ǁα.
Доказательство:
Т.к. MN — средняя линия трапеции, то по свойству средней линии MN ǁ AD , MN ǁВС =>
ВСǁα, AD ǁα по признаку параллельности прямой и плоскости ( Признак ( 
4. Прямая m параллельна диагонали BD ромба ABCD и не лежит в плоскости ромба. Докажите, что m и АС — скрещивающиеся прямые.
Доказательство:
Т.к. прямая m ǁ BD => m ǁ ABCD по признаку параллельности прямой и плоскости. По определению параллельных прямых m и BD лежат в одной плоскости, а т.к. АС 
S ABC — тетраэдр
Точки M , N и K — середины ребер DA , DB и DC .
Доказать: MNK ǁ ABCD .
Т.к. точки M , N и K — середины ребер DA , DB и DC => MN , NK и MK — средние линии Δ DAB , Δ DBC и Δ ADC соответственно. По свойству средней линии треугольника MN ǁ AB , NK ǁ BC и MK ǁ AC . По признаку параллельности плоскостей, MNK ǁ ABCD ( Признак (ǁ — ти плоскостей) : Если две пересекающиеся прямые одной плоскости, соответственно параллельны двум пересекающимся другой плоскости, то эти плоскости параллельны).
1. Построить параллелепипед ABCDA 1 B 1 C 1 D 1 и найти пары:
1) параллельные прямые к А D ;
2) скрещивающиеся прямые к A В.
1. Построить параллелепипед ABCDA 1 B 1 C 1 D 1 и найти пары:
1) параллельные прямые к C 1 D 1 ;
2) скрещивающиеся прямые к A 1 D 1 .
2. Точка М лежит на середине ребра AD тетраэдра DABC . Построить сечение тетраэдра плоскостью, проходящей через точку М параллельно плоскости В D С.
2. Точка М лежит на середине ребра D С тетраэдра DABC . Построить сечение тетраэдра плоскостью, проходящей через точку М параллельно плоскости А D В.
3. Точка М 

3. т. A 



4. Даны параллелограмм ABCD и трапеция ABEK с основанием EK , не лежащие в одной плоскости. Докажите, что AD ∸ EK .
4. Дан параллелограмм ABCD м точка S ∉ ABCD . Точки M и N — середины SB и SC . Доказать, что MN ∸ CD .
5. Дан параллелепипед ABCDA 1 B 1 C 1 D 1 . Точки K , L , M и N середины сторон AD , BC , B 1 C 1 и A 1 D 1 соответственно. Докажите плоскость KLMNǁABB 1 A 1 .
5. Дана четырехугольная пирамида S ABCD .
Точки K , L , M и N — середины ребер SA , SB , SC и SD соответственно. Доказать, что плоскость KLMN ǁ ABCD .
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

5.2.1 Пересекающиеся, параллельные и скрещивающиеся прямые; перпендикулярность прямых
Видеоурок: Параллельные прямые, перпендикулярные к плоскости
Лекция: Пересекающиеся, параллельные и скрещивающиеся прямые; перпендикулярность прямых

Если на плоскости имеются несколько прямых, то они либо рано или поздно пересекутся произвольно, либо под прямым углом, или же будут параллельными. Давайте же разберемся с каждым случаем.
Пересекающимися можно назвать те прямые, у которых будет хотя бы одна точка пересечения.
Вы спросите, почему хотя бы одна, не может же прямая пересечь другую прямую две или три раза. Вы правы! Но прямые могут полностью совпасть друг с другом. В таком случае общих точек будет бесконечное множество.

Параллельными можно назвать те прямые, которые никогда не пересекутся, даже на бесконечности.

Примеры параллельных прямых в жизни: два противоположных края экрана монитора, линии в тетрадях, а также многие другие части вещей, имеющих квадратную, прямоугольную и другие формы.
Когда хотят показать на письме, что одна прямая параллельная второй, то используют следующее обозначение a||b. Данная запись говорит, что прямая а параллельна прямой b.
При изучении данной темы важно понять еще одно утверждение: через некоторую точку на плоскости, которая не принадлежит данной прямой, можно провести единственную параллельную прямую. Но обратите внимание, снова поправка – на плоскости. Если рассматривать трехмерное пространство, то можно провести бесконечное множество прямых, которые не будут пересекаться, но будут скрещивающимися.
Утверждение, которое было описано выше, называется аксиомой о параллельности прямых.

Прямые можно назвать только в том случае перпендикулярными, если они пересекаются под углом, равным 90 градусов.
В пространстве через некоторую точку на прямой можно провести бесконечное множество перпендикулярных прямых. Однако, если речь идет о плоскости, то через одну точку на прямой можно провести единственную перпендикулярную прямую.

У любых скрещивающихся прямых есть вертикальные углы и смежные.
Если у углов, которые образованы двумя скрещивающимися прямыми, одна сторона общая, то они называются смежными:
Смежные углы в сумме дают 180 градусов.
Если же углы, образованные двумя скрещивающимися прямыми, не имеют общей стороны, то они называются вертикальными:
Вертикальные углы всегда равны.
Если же некоторая прямая пересекает две других прямых, то она называется секущей.
Частным случаем является секущая двух параллельных прямых:
🔥 Видео
Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Взаимное расположение прямых в пространстве. 10 класс.Скачать

Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

10 класс, 10 урок, Параллельные плоскостиСкачать

Перпендикулярные прямые. 6 класс.Скачать

Геометрия 10 класс (Урок№7 - Тетраэдр и параллелепипед.)Скачать

10 класс, 13 урок, ПараллелепипедСкачать

СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Стереометрия 10 класс. Часть 2 | Математика | TutorOnlineСкачать

10 класс, 24 урок, Прямоугольный параллелепипедСкачать

5 класс, 20 урок, Прямоугольный параллелепипедСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Сопряжение двух пересекающихся прямых. Урок 9. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Параллелепипед. 11 класс.Скачать

Как строить сечения параллелепипедаСкачать

10 класс, 14 урок, Задачи на построение сеченийСкачать












