На рисунке ef средняя линия треугольника kmn укажите вектор равный 2ef

Видео:8 класс, 25 урок, Средняя линия треугольникаСкачать

СРОЧНО . 70 баллов.
Точка D не лежит в плоскости ABC, точки E, F, G, K – середины отрезков AD, DC, BC и AB.
а) Докажите, что точки E, F, G, K лежат в одной плоскости.
б) Найдите периметр четырехугольника EFGK, если AC = 18 см, BD = 24 см.

Решение. а) EF – средняя линия треугольника __________, поэтому EF∥ _____ и EF = ______; KG – средняя _________________________ и потому _______________.
Следовательно, EF∥ _____, т.е. точки E, F, G, K лежат на параллельных прямых, а значит, лежат в одной __________________.
б) Четырехугольник EFGK – параллелограмм, так как ________________________, причем EF = ____________, EK = _______________, а потому P_EFGK=____________________________.
Ответ. б) ____________

Видео:Геометрия 8. Средняя линия трапеции. Средняя линия треугольника. Задачи.Скачать

Решение треугольников онлайн

С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.

Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:

1. Три стороны треугольника.
2. Две стороны треугольника и угол между ними.
3. Две стороны и угол противостоящий к одному из этих сторон треугольника.
4. Одна сторона и любые два угла.

Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.

Видео:№126. На рисунке 74 ∠DAB = ∠CBA, ∠CAB = ∠DBA, AC = 13 см. Найдите BD.Скачать

Решение треугольника по трем сторонам

Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем .

(1)

(2)

Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения

.

Пример 1. Известны стороны треугольника ABC: Найти (Рис.1).

Решение. Из формул (1) и (2) находим:

.

.

, .

И, наконец, находим угол C:

Видео:Геометрия 8. Урок 7 - Средняя линия треугольника и трапецииСкачать

Решение треугольника по двум сторонам и углу между ними

Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.

Найдем сторону c используя теорему косинусов:

.

.

Далее, из формулы

.

.

(3)

Далее из (3) с помощью калькулятора находим угол A.

Поскольку уже нам известны два угла то находим третий:

.

Пример 2. Известны две стороны треугольника ABC: и (Рис.2). Найти сторону c и углы A и B.

Решение. Иcпользуя теорму косинусов найдем сторону c:

,

.

Из формулы (3) найдем cosA:

.

Поскольку уже нам известны два угла то находим третий:

.

Видео:Треугольник, свойства треугольника, линии в треугольникеСкачать

Решение треугольника по стороне и любым двум углам

Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.

Так как, уже известны два угла, то можно найти третий:

.

Далее, для находждения сторон b и c воспользуемся тероемой синусов:

, .

, .

Пример 3. Известна одна сторона треугольника ABC: и углы (Рис.3). Найти стороны b и c и угол С.

Решение. Поскольку известны два угла, то легко можно найти третий угол С:

Найдем сторону b. Из теоремы синусов имеем:

Найдем сторону с. Из теоремы синусов имеем:

🎬 Видео

ОГЭ/База Все прототипы задач с треугольникамиСкачать

Средняя линия треугольника | Задачи 11-20 | Решение задач | Волчкевич | Уроки геометрии 7-8 классСкачать

Задание 5 ОГЭ по математикеСкачать

№194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертежногоСкачать

7 задание егэ математика проф На рисунке изображен график производной функцииСкачать

№786. Отрезки AA1, ВВ1 и СС1 — медианы треугольника ABC. Выразите векторы AA1, BB1, СС1Скачать

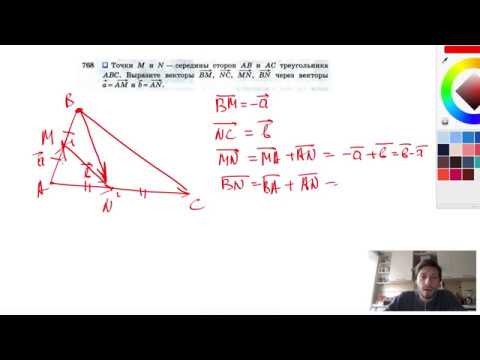
№768. Точки М и N — середины сторон АВ и АС треугольника ABC. Выразите векторыСкачать

8246Скачать

A2. Информационные модели ЕГЭ по информатикеСкачать

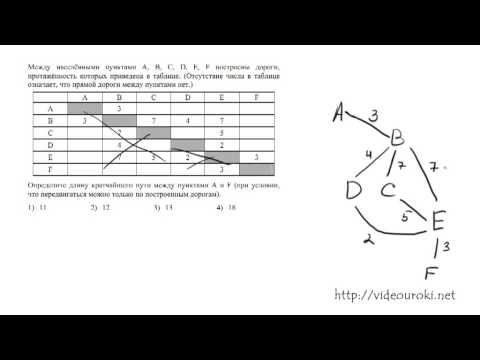
Задача 7 ЕГЭ по математике. Урок 15.Скачать

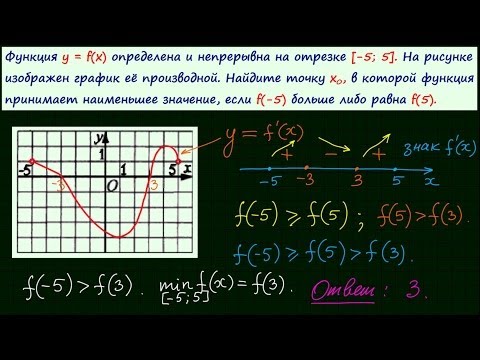
№17. На рисунке 17 точки М, N, Q и Р — середины отрезков DB, DC, АС и АВ.Скачать

Задание 3 ЕГЭ по математике. Урок 11Скачать

Задача №255 [НЕДЕТСКАЯ ГЕОМЕТРИЯ #1]Скачать

№94. На рисунке 52 AB=АС, ∠1=∠2. а) Докажите, что треугольники ABD и ACD равны;Скачать