На рисунке 2 прямые м и н параллельны точки а и б соответственно принадлежат

Геометрия | 10 — 11 классы

На рисунке 2 прямые m и n пересекаются в точке М, А € m ; В € n ; b лежит в плоскости α , а b.

Каково взаимное положение прямых b и с?

В задаче ничего не сказано про прямую с, пожэтому две возможности.

Если с принадлежит плоскостям МАВ и альфа, то она является линией пересечения плоскостей и однозначно параллельна прямой в, так как если прямая

параллельна плоскости и содержится в другой плоскости, пересекающей

первую, то она параллельна линии пересечения этих плоскостей.

Если прямая с не является линией пересечения плоскостей, то она может быть параллельна в, но может и пересекаться с ней.

Единственное, чего она не может, быть скрещивающейся с прямой в, так как лежит с ней в одной плоскости.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Если прямая и плоскость имеют только одну общую точку, то прямая а)пересекает плоскость ; б)лежит в плоскости ; в)параллельна плоскости?

Если прямая и плоскость имеют только одну общую точку, то прямая а)пересекает плоскость ; б)лежит в плоскости ; в)параллельна плоскости.

Видео:Прямые m и n параллельны. Найдите ∠3, если ∠1=24°, ∠2=90° | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

Прямая а параллельна плоскости альфа , точка М и прямая с лежит в плоскости альфа (м не принадлежит с) Через точку М проведена прямая в, параллельная а?

Прямая а параллельна плоскости альфа , точка М и прямая с лежит в плоскости альфа (м не принадлежит с) Через точку М проведена прямая в, параллельная а.

Каково взаимное положение в и с?

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

10 КЛАСС?

На рисунке 2 прямые m и n пересекаются в точке М, А € m ; В € n ; b лежит в плоскости α ,

Каково взаимное положение прямых b и с?

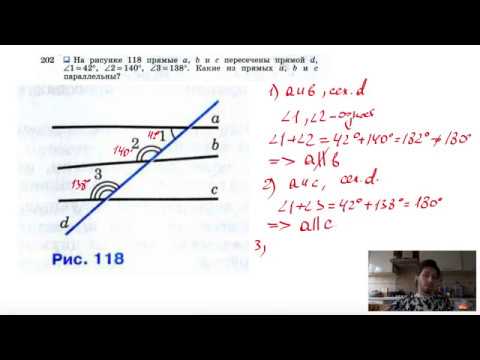
Видео:№202. На рисунке 116 прямые а, b и с пересечены прямой d, ∠1=42°, ∠2=140°, ∠3=138°. Какие из прямыхСкачать

Плоскости «альфа» и «бета»пересекаются по прямой а?

Плоскости «альфа» и «бета»пересекаются по прямой а.

Прямая b, лежащая в плоскости «бета», пересекает плоскость «альфа»в точке А.

Где лежит точка А?

Видео:Принадлежность прямой плоскостиСкачать

В каком случае 3 точки в пространстве не определяют положение плоскости, проходящей через эти точки?

В каком случае 3 точки в пространстве не определяют положение плоскости, проходящей через эти точки?

Могут ли 2 различные плоскости иметь только одну общую точку?

Точка М не лежит на прямой а.

Через точку М проводят прямые , пересекающие прямую а.

Лежат ли эти прямые в одной плоскости?

Видео:Взаимное расположение прямых в пространстве. 10 класс.Скачать

Прямая а лежит в плоскости альфа?

Прямая а лежит в плоскости альфа.

Плоскость бета пересекает плоскость альфа по прямой б.

Известно, что прямая а пересекает плоскость бета в точке Б.

Где лежит точка Б?

Видео:Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

Плоскости альфа и бета параллельны прямая m пересекает плоскость бета?

Плоскости альфа и бета параллельны прямая m пересекает плоскость бета.

Каково взаимное положение m и плоскости альфа.

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Плоскость альфа и бетта пересекаются по прямой m?

Плоскость альфа и бетта пересекаются по прямой m.

Прямая а лежит в плоскостях альфа, а b в плоскотях бетта.

Какие возможны взаимные положения прямых a и b.

Сделайте рисунок пожалуйста и поясните.

Видео:Точка, прямая и отрезок. 1 часть. 7 класс.Скачать

Даны пересекающиеся плоскости альфа и бета?

Даны пересекающиеся плоскости альфа и бета.

Прямая с лежит в плоскости бета и пересекает плоскость альфа в точке С.

Прямая d лежит в плоскости альфа и пересекает плоскость бета в точке D.

По какой прямой пересекаются плоскости альфа и бета?

Помогите пж — та с задачей.

Видео:Параллельные прямые. 6 класс.Скачать

Прямые a и b пересекаются?

Прямые a и b пересекаются.

Прямая a пересекает плоскость альфа.

Каково взаимное расположение прямой b и плоскости альфа.

На этой странице находится вопрос На рисунке 2 прямые m и n пересекаются в точке М, А € m ; В € n ; b лежит в плоскости α , а b?. Здесь же – ответы на него, и похожие вопросы в категории Геометрия, которые можно найти с помощью простой в использовании поисковой системы. Уровень сложности вопроса соответствует уровню подготовки учащихся 10 — 11 классов. В комментариях, оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С ними можно обсудить тему вопроса в режиме on-line. Если ни один из предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой строке, расположенной вверху, и нажмите кнопку.

Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Контрольные и самостоятельные работы для обучающихся 10-11 классов. Некоторые работы составлены на основе или с элементами заданий Открытого банка ЕГЭ.

Видео:№40. На скрещивающихся прямых а и b отмечены соответственно точки М и N.Скачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Выбранный для просмотра документ 10 Ср Определение тригонометрических функций.docx

10 класс. Самостоятельная работа. « Определение тригонометрических функций».

Выбранный для просмотра документ 10 кл Кр Аксиомы стереометрии и их следствия.docx

Контрольная работа № 1. Аксиомы стереометрии и их следствия.

Точка М лежит вне плоскости α , а точки А, В, С принадлежат этой плоскости.

Принадлежит ли точка Е плоскости α ?

Укажите прямую пересечения плоскостей α и АВМ.

Принадлежит ли прямая АС плоскости МВС?

Точка М лежит вне плоскости α , а точки А, В, С принадлежат этой плоскости.

Принадлежит ли точка F плоскости α ?

Укажите прямую пересечения плоскостей ABM и ВМ C .

Принадлежит ли прямая А B плоскости МВС?

Выбери верный ответ.

Плоскость, притом только одна, проходит через а) любые три точки; б) любые три точки , лежащие на одной прямой; в) любые три точки , не лежащие на одной прямой.

Выбери верный ответ.

Если две точки прямой принадлежат плоскости, то прямая

а) пересекает плоскость; б) лежит в плоскости; в) параллельна плоскости.

Лучи МА, МВ и МС лежат в одной плоскости и пересекают плоскость α в точках А, В, С. Докажите, что точки А, В, С лежат на одной прямой.

Плоскости α и β пересекаются по прямой l . Прямая m лежит в плоскости α. Постройте точку пересечения прямой m и плоскости β. Обоснуйте построение.

Прямые m и n пересекаются в точке М. А Є m , В Є n , прямая b лежит в плоскости α, a || b . Каково взаимное расположение прямых b и с? Ответ обоснуйте.

Прямые m и n параллельны. Точки А и В co ответственно принадлежат прямым m и n , прямая b лежит в плоскости α, α|| b . Каково взаимное расположеение прямых b и c ? Ответ обоснуйте

Прямые Е N и КМ не лежат в одной плоскости. Могут ли прямые Е N и KM пересекаться? Ответ обоснуйте.

Точки К, М, Р, Т не лежат в одной плоскости. Могут ли прямые КМ и РТ пересекаться? Ответ обоснуйте.

Могут ли две различные плоскости иметь только две общие точки? Ответ обоснуйте.

Могут ли две различные плоскости иметь только одну общую точку? Ответ обоснуйте.

Каково взаимное расположение прямых: а) AD ₁ и MN ; б) AD ₁ и BC _1; в) MN и DC ?

Каково взаимное расположение прямых: а) A ₁ D и MN ; б) A ₁ D и B ₁ C _; в) MN и А ₁ В ₁ ?

Выбранный для просмотра документ 10 кл Кр Параллельность прямых и плоскостей.docx

Контрольная работа по теме «Параллельность прямых и плоскостей».

Через концы отрезка АВ и его середину М проведены параллельные прямые, пересекающие некоторую плоскость в точках А ₁ , М ₁ , В ₁ . Найдите длину отрезка ММ ₁ , если отрезок АВ не пересекает плоскость и АА ₁ =15,2 см,

Через концы отрезка АВ и его середину М проведены параллельные прямые, пересекающие некоторую плоскость в точках А ₁ , М ₁ , В ₁ . Найдите длину отрезка ММ ₁ , если отрезок АВ не пересекает плоскость и АА ₁ =17,4 см, ВВ ₁ = 9,8 см.

Через концы отрезка АВ и его середину М проведены параллельные прямые, пересекающие некоторую плоскость в точках А ₁ , М ₁ , В ₁ . Найдите длину отрезка ММ ₁ , если отрезок АВ пересекает плоскость и АА ₁ =8,4 см,

Через концы отрезка АВ и его середину М проведены параллельные прямые, пересекающие некоторую плоскость в точках А ₁ , М ₁ , В ₁ . Найдите длину отрезка ММ ₁ , если отрезок АВ пересекает плоскость и АА ₁ =9,8 см, ВВ ₁ = 17,4 см.

Через конец А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые, пресекающие плоскость в точках В ₁ и С ₁ . Найдите длину отрезка ВВ ₁ , если СС ₁ = 25 см, АС : ВС = 2 : 3.

Через конец А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые, пресекающие плоскость в точках В ₁ и С ₁ . Найдите длину отрезка ВВ ₁ , если АВ=14 см, АС : ВС = 2 : 5.

Дан треугольник АВС. Плоскость, параллельная прямой АВ, пересекает сторону АС этого треугольника в точке А ₁ , а сторону ВС – в точке В ₁ . Найдите длину отрезка А ₁ В ₁ , если АВ = 16, АА ₁ : А ₁ С = 5 : 3.

Дан треугольник АВС. Плоскость, параллельная прямой АВ, пересекает сторону АС этого треугольника в точке А ₁ , а сторону ВС – в точке В ₁ . Найдите длину отрезка А ₁ В ₁ , если АВ = 30, АА ₁ : АС = 2 : 3

Контрольная работа по теме «Параллельность прямых и плоскостей».

Через концы отрезка АВ и его середину М проведены параллельные прямые, пересекающие некоторую плоскость в точках А ₁ , М ₁ , В ₁ . Найдите длину отрезка ММ ₁ , если отрезок АВ не пересекает плоскость и АА ₁ =15,2 см,

Через концы отрезка АВ и его середину М проведены параллельные прямые, пересекающие некоторую плоскость в точках А ₁ , М ₁ , В ₁ . Найдите длину отрезка ММ ₁ , если отрезок АВ не пересекает плоскость и АА ₁ =17,4 см, ВВ ₁ = 9,8 см.

Через концы отрезка АВ и его середину М проведены параллельные прямые, пересекающие некоторую плоскость в точках А ₁ , М ₁ , В ₁ . Найдите длину отрезка ММ ₁ , если отрезок АВ пересекает плоскость и АА ₁ =8,4 см,

Через концы отрезка АВ и его середину М проведены параллельные прямые, пересекающие некоторую плоскость в точках А ₁ , М ₁ , В ₁ . Найдите длину отрезка ММ ₁ , если отрезок АВ пересекает плоскость и АА ₁ =9,8 см, ВВ ₁ = 17,4 см.

Через конец А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые, пресекающие плоскость в точках В ₁ и С ₁ . Найдите длину отрезка ВВ ₁ , если СС ₁ = 25 см, АС : ВС = 2 : 3.

Через конец А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые, пресекающие плоскость в точках В ₁ и С ₁ . Найдите длину отрезка ВВ ₁ , если АВ=14 см, АС : ВС = 2 : 5.

Дан треугольник АВС. Плоскость, параллельная прямой АВ, пересекает сторону АС этого треугольника в точке А ₁ , а сторону ВС – в точке В ₁ . Найдите длину отрезка А ₁ В ₁ , если АВ = 16, АА ₁ : А ₁ С = 5 : 3.

Дан треугольник АВС. Плоскость, параллельная прямой АВ, пересекает сторону АС этого треугольника в точке А ₁ , а сторону ВС – в точке В ₁ . Найдите длину отрезка А ₁ В ₁ , если АВ = 30, АА ₁ : АС = 2 : 3

Выбранный для просмотра документ 11 Кр 1 Многоганники с эл-тами ЕГЭ 5 вар .docx

Контрольная работа по теме «Многогранники» с элементами ЕГЭ. Вариант 5

№ 1 (B9). В правильной треугольной пирамиде медианы основания пересекаются в точке . Площадь треугольника равна 4; объем пирамиды равен 6. Найдите длину отрезка .

№ 2 (B9). В правильный четырехугольной пирамиде точка – центр основания, – вершина, =12, =18. Найдите боковое ребро

№ 3 (В9). В правильной треугольной пирамиде – середина ребра , – вершина. Известно, что =7, а площадь боковой поверхности пирамиды равна 42. Найдите длину отрезка .

№ 4 (B9). В правильной четырехугольной пирамиде точка — центр основания, вершина, , . Найдите длину отрезка .

№ 5 (В9). Найдите квадрат расстояния между вершинами C и A ₁ прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA ₁ =3.

№ 6 (B9). Найдите квадрат расстояния между вершинами и многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

№ 7 (B11). Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.

№ 8 (B11). Объем параллелепипеда равен 12. Найдите объем треугольной пирамиды .

Выбранный для просмотра документ 11 Кр 1 Многоганники с эл-тами ЕГЭ 1 вар .docx

Контрольная работа по теме «Многогранники»

(с элементами Открытого банка ЕГЭ). Вариант 1.

№ 1 (B9). В правильной треугольной пирамиде медианы основания пересекаются в точке . Площадь треугольника равна 9; объем пирамиды равен 6. Найдите длину отрезка .

№ 2 (B9). В правильный четырехугольной пирамиде точка – центр основания, – вершина, , . Найдите боковое ребро .

№ 3 (В9). В правильной треугольной пирамиде точка – середина ребра , – вершина. Известно, что =3, а площадь боковой поверхности пирамиды равна 45. Найдите длину отрезка .

№ 4 (B9). В правильной четырехугольной пирамиде точка — центр основания, вершина, , Найдите боковое ребро .

№ 5 (В9). В прямоугольном параллелепипеде известно, что Найдите длину ребра .

№ 6 (B9). Найдите тангенс угла многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

№ 7 (B11). Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.

№ 8 (B11). Найдите объем параллелепипеда , если объем треугольной пирамиды равен 3.

Видео:Пересекающиеся и параллельные прямые, лучи, отрезки. Задачи. Геометрия. Математика 2 класс.Скачать

Г10(I)-3. Параллельность плоскостей. Тесты

Геометрия 10 класс. Глава I. Тест 3.

Вариант 1.

1. Выбрать верные утверждения.

1) Две плоскости называются параллельными, если они не имеют ни одной общей точки.

2) Если две плоскости пересечены третьей, то линии их пересечения параллельны.

3) Отрезки параллельных прямых, заключённые между параллельными плоскостями, равны.

A) 1; 2; 3; B) 1; 2; C) 1; 3; D) 2; 3.

2. На рисунке 1 точки: Е-середина АМ, К-середина ВМ, Р-середина СМ. Площадь треугольника ЕКР равна 24 см 2 . Найти площадь треугольника АВС.

A) 96 см 2 ; B) 64 см 2 ; C) 72 см 2 ; D) 48 см 2 .

3. Параллельные плоскости α и β пересекают стороны угла РМК в точках А, В, Е и С, как показано на рисунке 2. Известно, что МВ=2,5АМ, АЕ=18 см. Найти ВС.

A) 40 см; B) 45 см; C) 36 см; D) 42 см.

4. На рисунке 3 точки А, В и С лежат в плоскости α, точки М, Р и К в плоскости β. Отрезки АК=СМ и ВР имеют общую середину О. Величина угла АОС составляет 60°, МК=9 см. Найти АК.

A) 20 см; B) 18 см; C) 16 см; D) 12 см.

Вариант 2.

1. Выбрать верные утверждения.

1) Возможны два случая взаимного расположения плоскостей: а) две плоскости пересекаются по прямой; б) две плоскости параллельны.

2) Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

3) Две плоскости называются параллельными, если они не пересекаются.

A) 1; 2; 3; B) 1; 2; C) 1; 3; D) 2; 3.

2. На рисунке 1 точки: Е-середина АМ, К-середина ВМ, Р-середина СМ. Площадь треугольника АВС равна 120 см 2 . Найти площадь треугольника ЕКР.

A) 60 см 2 ; B) 40 см 2 ; C) 30 см 2 ; D) 24 см 2 .

3. Параллельные плоскости α и β пересекают стороны угла РМК в точках А, В, Е и С, как показано на рисунке 2. Известно, что МС=3,5МЕ, ВС=21 см. Найти АЕ.

A) 9 см; B) 6 см; C) 7 см; D) 12 см.

4. На рисунке 3 точки А, В и С лежат в плоскости α, точки М, Р и К в плоскости β. Отрезки АК=СМ и ВР имеют общую середину О. Величина угла МОК составляет 60°, МС=24 см. Найти АС.

A) 20 см; B) 18 см; C) 16 см; D) 12 см.

Вариант 3.

1. Выбрать верные утверждения.

1) Если прямая а пересекает плоскость α, то она пересекает также любую плоскость, отличную от плоскости α.

2) Если две пересекающиеся прямые а и с плоскости α параллельны плоскости β, то плоскости α и β пересекаются.

3) Если плоскости α и β параллельны, а прямая с лежит в плоскости α, то прямая с параллельна плоскости β.

4) Через точку А, не лежащую в плоскости α можно провести плоскости, параллельные плоскости α.

A) 1; B) 2; C) 3; D) 4.

2. На рисунке 1 плоскости АВС и МКР параллельны, АМ:МО=2:5, площадь треугольника МРК равна 50 см 2 . Найти плоскость треугольника АВС.

A) 75 см 2 ; B) 100 см 2 ; C) 96 см 2 ; D) 98 см 2 .

3. Параллельные плоскости α и β пересекают стороны угла АВС в точках М, К, Р и Е как показано на рисунке 2. Известно, что ВР=3,5МР, ВМ=12,5 см, МК=25 см. Найти РЕ.

A) 35 см; B) 36 см; C) 42 см; D) 34 см.

4. На рисунке 3 точки А, В и С лежат в плоскости α, точки М, Р и К в плоскости β. Отрезки АК=СМ и ВР имеют общую середину О, АК=17 см, МК=8 см. Найти СК.

A) 25 см; B) 15 см; C) 20 см; D) 35 см.

Вариант 4.

1. Выбрать верные утверждения.

1) Если плоскости α и β параллельны, а прямая с лежит в плоскости α, то прямая с пересечёт плоскость β.

2) Если плоскости α и β параллельны плоскости γ, то плоскости α и β параллельны.

3) Если точка А не лежит в плоскости пересекающихся прямых m и n, то через неё нельзя провести плоскость, параллельную прямым m и n.

4) Если прямая а параллельна одной из двух параллельных плоскостей, то она лежит в другой плоскости.

A) 1; B) 2; C) 3; D) 4.

2. На рисунке 1 плоскости АВС и МКР параллельны, ОК:СК=7:3, площадь треугольника АВС равна 100 см 2 . Найти плоскость треугольника МРК.

A) 50 см 2 ; B) 25 см 2 ; C) 48 см 2 ; D) 49 см 2 .

3. Параллельные плоскости α и β пересекают стороны угла АВС в точках М, К, Р и Е как показано на рисунке 2. Известно, что ВЕ=2,5КЕ, ВК=4,5 см, РЕ=15 см. Найти МК.

A) 5 см; B) 6 см; C) 9 см; D) 8 см.

4. На рисунке 3 точки А, В и С лежат в плоскости α, точки М, Р и К в плоскости β. Отрезки АК=СМ и ВР имеют общую середину О. АС=7 см, АМ=24 см. Найти АК.

A) 25 см; B) 15 см; C) 20 см; D) 35 см.

1) Возможны два случая взаимного расположения плоскостей: а) две плоскости пересекаются по прямой; б) две плоскости не имеют ни одной общей точки.

2) Две плоскости называются параллельными, если они не пересекаются.

3) Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

4) Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.

5) Отрезки параллельных прямых, заключённые между параллельными плоскостями, равны.

📺 Видео

Геометрия 7 класс (Урок№33 - Повторение. Параллельные и перпендикулярные прямые.)Скачать

7 класс, 30 урок, Углы с соответственно параллельными или перпендикулярными сторонамиСкачать

Параллельные прямые (задачи).Скачать

ГДЗ по геометрии | Номер 555 Геометрия 8 класс Атанасян Л.С. | Подробный разборСкачать

Как строить сечения параллелепипедаСкачать

№86. Даны две пересекающиеся прямые а и b и точка А, не лежащая на этих прямых.Скачать