На плоскости проведены 5 прямых никакие две из которых не параллельны

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Комбинаторная задача о числе точек пересечения прямых

Известная комбинаторная задача 1) Виленкин Н.Я., Виленкин А.Н., Виленкин П.А. Комбинаторика. – М.: МЦНМО, 2006. 2) Смирнова И.М., Смирнов В.А. Комбинаторные задачи по геометрии (Библиотечка «Первого сентября». Математика. Вып. 5 (11)). – М.: Чистые пруды, 2006.

Задача о количестве точек пересечения n прямых На плоскости проведены n прямых, среди которых нет ни одной пары параллельных прямых и ни одной тройки прямых, пересекающихся в одной точке. Найти число точек пересечения таких прямых. Пример. n=5, 10 точек пересечения

Цели работы 1) обобщить одну из известных комбинаторных задач по геометрии и получить полное решение новых задач; 2) показать возможность применения метода рекуррентных соотношений для решения комбинаторных задач по геометрии.

Задача 1. Наличие параллельных прямых На плоскости провели n прямых, среди которых k параллельных прямых и никакие три прямые не проходят через одну точку. Сколько точек пересечения прямых получилось? Пример 1. n=8, k=3 25 точек пересечения Пример 2. n=8, k=4 22 точки пересечения

О методе рекуррентных соотношений Метод сведения комбинаторной задачи к аналогичной задаче для меньшего числа предметов с помощью некоторого соотношения называется методом рекуррентных соотношений. Пользуясь рекуррентным соотношением, задачу с n предметами можно свести к задаче с n–1 предметом, потом к задаче с n–2 предметами и т.д. Во многих случаях из рекуррентного соотношения удается получить явную формулу для решения комбинаторной задачи.

Решение задачи №1 1) Наглядное нахождение закономерностей 2) Нахождение формулы, позволяющей найти количество точек пересечения по любым значениям n и k

Нахождение числа точек пересечения

Таблица и рекуррентные соотношения k m Параллельные прямые 2 3 4 5 Прямые общего положения 1 2 3 4 5 2 5 7 9 11 3 9 12 15 18 4 14 18 22 26 5 20 25 30 35

Задача 2. Наличие пар параллельных прямых На плоскости провели n прямых, среди которых k пар параллельных прямых (прямые в разных парах непараллельные) и никакие три прямые не проходят через одну точку. Сколько точек пересечения прямых получилось? Пример 1. n=5, k=2 19 точек пересечения Пример 2. n=6, k=3 33 точки пересечения

Решение задачи №2 1) Наглядное нахождение закономерностей 2) Нахождение формулы, позволяющей найти количество точек пересечения по любым значениям n и k

Нахождение числа точек пересечения

Таблица и рекуррентные соотношения k m Пары параллельных прямых 2 3 4 5 Прямые общего положения 1 2 8 18 32 2 5 13 25 41 3 9 19 33 51 4 14 26 42 62 5 20 34 52 74

СПАСИБО ЗА ВНИМАНИЕ!

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 967 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 342 человека из 71 региона

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 690 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

Именно учебная деятельность как универсальный способ учения определяет особую деятельностную образовательную технологию: переход от «ситуации успеха» к «ситуации разрыва» через рефлексивную оценку (постановку учебной задачи); моделирование и конструирование (этап решения учебной задачи); продвижение от диагностической работы на «входе» через коррекцию к диагностической работе на «выходе» (этап решения частных задач); проверочная работа как переход от одной учебной задачи к другой (констатирующая оценка); перенос способов действий и средств в квазиреальные ситуации (этап решения проектных задач).

Основной принцип построения деятельностной технологии — цикличность (ритмичность) разворачивания образовательного процесса, в котором выделяются три цикла: пятилетний, годовой и тематический.

В рамках реализации деятельностной технологии необходимо особое внимание уделять контрольно-оценочной деятельности. Целесообразно развести контроль и оценку как учебные действия младших школьников и контроль и оценку как педагогические действия.

При деятельностной технологии педагогом создаются разные образовательные пространства:

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

На плоскости проведены 5 прямых никакие две из которых не параллельны

Задача 1: 1995-значное число заканчивается на 1, и всякое двузначное число, образованное его соседними цифрами, идущими в том же порядке, делится либо на 17, либо на 23. Какова первая цифра этого числа? Делится ли оно на 3? На 9?

Решение:

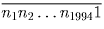
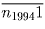
Пусть данное число имеет вид: . Выпишем все двузначные числа, делящиеся на 17 или на 23 – 51,92,23,34,85,46,17, 68,69, и заметим, что последняя цифра этих чисел однозначно определяет само число. Тогда так как делится либо на 17, либо на 23 n ₁₉₉₄ = 5. Аналогично, n ₁₉₉₃ = 8, n ₁₉₉₂ = 6, и.т.д. Таким образом, данное число имеет вид: 4692346 92346851, а его первая цифра – 4. Подсчитаем сумму цифр числа: 10 + 24*399 + 14 = 9600. Следовательно, оно делится на 3, и не делится на 9.

Задача 2: Для всех значений a, b и c решить систему:

Решение:

Сложив первое уравнение со вторым и вычтя третье, получаем: (x + y – z)² = a + b – c. Если a + b – c 0, то .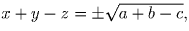

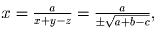
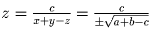
Ответ: если a + b – c 0, то решений два: , , .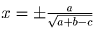

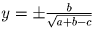
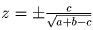
Задача 3: На плоскости дан выпуклый многоугольник. Из середины каждой его стороны перпендикулярно к ней выходит вектор, направленный наружу многоугольника и равный по длине половине стороны из которой он выходит. Докажите, что сумма всех таких векторов равна нулю.

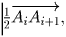
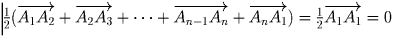
Решение: Пусть дан многоугольник A ₁ A ₂ A _n . Повернем все векторы на 90° по часовой стрелке. Тогда вектор их суммы также окажется повернут на 90° по часовой стрелке. С другой стороны, вектор, выходящий из стороны A _i A _{i + 1} многоугольника, перейдет в вектор а сумма всех таких векторов равна .

Задача 4: На плоскости проведено семь прямых, никакие две из которых не параллельны. Докажите, что из них можно выбрать две, угол между которыми не превосходит 26°.

Решение:

Без ограничения общности полагаем, что все прямые проходят через одну точку. Эти прямые разбивают плоскость на 14 углов. Так как 360:14

Видео:Параллельные прямые. 6 класс.Скачать

Максим проводит на плоскости прямые так , что никакие 2 из них не параллельны и никакие 3 не проходят через одну точку ?

Математика | 5 — 9 классы

Максим проводит на плоскости прямые так , что никакие 2 из них не параллельны и никакие 3 не проходят через одну точку .

Он хочет чтобы все треугольники образованные этими прямыми были тупоугольными .

Какое наибольшее число прямых он сможет провести?

Видео:Параллельность прямых. 10 класс.Скачать

Через каждые 2 точки проводиться прямая?

Через каждые 2 точки проводиться прямая.

Сколько получиться прямых, если даны : 4 точки, никакие 3 из которых не лежат на 1 прямой?

Видео:10 класс, 5 урок, Параллельность трех прямыхСкачать

На плоскости через точку А проведено 5 прямых?

На плоскости через точку А проведено 5 прямых.

Какое наибольшее кол — во прямых углов может при этом образоваться?

Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Какие из нижеприведённых утверждений верные , а какие нет ?

Какие из нижеприведённых утверждений верные , а какие нет ?

1 Через точку лежащую вне прямой , можно провести несколько прямых , параллельных этой прямой .

2 Если две прямые на плоскости не перпеендикулярны третьей прямой то они пересекаются.

3 Через точку , лежащую вне прямой , можно провести только одну прямую , параллельную этой прямой .

4 Если две прямые на плоскости перпендикулярны третьей прямой , то они паралельны.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Через каждые две точки проводится прямая?

Через каждые две точки проводится прямая.

Сколько получится прямых , если даны : 1) 3 точки, не лежащие на одной прямой.

2) 4 точки, никакие три из которых не лежат на одной прямой?

Видео:10 класс, 10 урок, Параллельные плоскостиСкачать

Через каждые 2 точки проводится прямая?

Через каждые 2 точки проводится прямая.

Сколько получится прямых если даны : 1)3 точки не лежащие на одной прямой ; 2)4 точки никакие три из которых не лежат на одной прямой.

Видео:ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ перпендикулярные к плоскости 10 классСкачать

Вася проводит на плоскости прямые так, что никакие две из них не параллельны и никакие три не проходят через одну точку?

Вася проводит на плоскости прямые так, что никакие две из них не параллельны и никакие три не проходят через одну точку.

Он хочет, чтобы все треугольники, образованные этими прямыми, были треугольными.

Какое наибольшее число прямых он сможет провести?

А) 7 б) 6 в) 5 г) 4 д) сколько угодно.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Через точку одной из параллельных плоскостей проведена прямая параллельная второй плоскости?

Через точку одной из параллельных плоскостей проведена прямая параллельная второй плоскости.

Верно ли, что это прямая лежит в первой плоскости?

Видео:Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

Через заданную точку плоскости можно провести не более одной прямой?

Через заданную точку плоскости можно провести не более одной прямой?

Видео:7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

Какие из следующих утверждений верны?

Какие из следующих утверждений верны?

1) Любая биссектриса равнобедренного треугольника является его медианой 2)Через точку, не лежащую на данной прямой.

Можно провести прямую, параллельную этой прямой.

3)В любом тупоугольном треугольнике есть острый угол.

Видео:Точка, прямая и отрезок. 1 часть. 7 класс.Скачать

Какое наибольшее число плоскостей можно провести через различные пары из четырёх параллельных прямых ?

Какое наибольшее число плоскостей можно провести через различные пары из четырёх параллельных прямых ?

Вы перешли к вопросу Максим проводит на плоскости прямые так , что никакие 2 из них не параллельны и никакие 3 не проходят через одну точку ?. Он относится к категории Математика, для 5 — 9 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Математика. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.

I день х кг II день 2х кг III день (2, 5 * 2х ) кг Всего 323, 2 кг Уравнение. Х + 2х + 2, 5 * 2х = 323, 2 х + 2х + 5х = 323, 2 (1 + 2 + 5) * х = 323, 2 8х = 323, 2 х = 323, 2 : 8 х = 40, 4 (кг) I день 40, 4 * 2 = 80, 8 (кг) II день 80, 8 * 2, 5 = 20..

45 мин — 2700 27600 в 6 часах 10810 в 3 часах и 10 минутах.

45 мин = 2700 с 6 ч = 360 мин = 21600 с 3 ч 10 мин = 190 мин = 11400.

Там только на 2 можно умножить. Так что вот 35× 2_ + 70 140_ 210.

1)100 — 20 = 80 2)600•0. 8 = 480 Ответ : 480человек.

1 : 45 = 1 / 45 делает 1 бригада за 1 дн 1 : 90 = 1 / 90 делает 2 бригада за 1 дн 1 / 45 + 1 / 90 = 1 / 30 делают 2 бригады за 1 дн 1 / 30 : 1 = 30 дн делают.

600 / 10 * 2 = 120 600 — 120 = 480.

1 : 45 = 1 / 45 делает 1 бригада за 1 дн 1 : 90 = 1 / 90 делает 2 бригада за 1 дн 1 / 45 + 1 / 90 = 1 / 30 делают 2 бригады за 1 дн 1 / 30 : 1 = 30 дн делают.

1) 34 × 2 = 68 см 2) 122 — 68 = 54 см 3) 54 : 2 = 27 см Ответ : 27 см.

📸 Видео

Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Плоскость. Пересекающиеся прямые. 6 класс.Скачать

10 класс, 16 урок, Параллельные прямые, перпендикулярные к плоскостиСкачать

10 класс, 6 урок, Параллельность прямой и плоскостиСкачать

Параллельные и скрещивающиеся прямые. СтереометрияСкачать

10 класс, 4 урок, Параллельные прямые в пространствеСкачать