Могут ли прямые быть параллельными если они не лежат в одной плоскости

Две прямые в пространстве называются параллельными , если они лежат в одной плоскости и не пересекаются. Прямые, которые не пересекаются и не лежат в одной плоскости называются скрещивающимися. Прямая и плоскость в пространстве называются параллельными, если они не пересекаются.

Прямая параллельна плоскости, если она параллельна какой-нибудь прямой, лежащей в этой плоскости.

Две плоскости называются параллельными, если они не пересекаются.

Если две параллельные плоскости пересекаются третьей плоскостью, то прямые пересечения плоскостей параллельны. Через точку, не лежащую в данной плоскости, можно провести параллельную плоскость, и притом только одну.

, так как

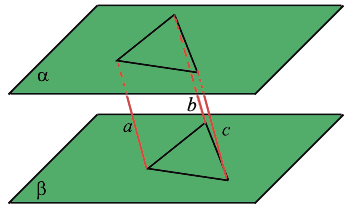
Отрезки параллельных прямых между параллельными плоскостями равны.

= =

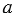
Прямые в пространстве называются перпендикулярными, если они пересекаются под прямым углом. Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой в плоскости, проходящей через точку их пересечения.

Прямая, пересекающая плоскость, перпендикулярна плоскости, если она перпендикулярна двум прямым в плоскости, проходящим через точку их пересечения.

.

Через каждую точку плоскости можно провести перпендикулярную ей прямую, и только одну. Все прямые, перпендикулярные данной плоскости, параллельны.

Перпендикуляр, опущенный из данной точки на данную плоскость, — это отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, которая перпендикулярна плоскости. Основание перпендикуляра — это его конец, лежащий в плоскости.

Расстояние от точки до плоскости — это длина перпендикуляра, опущенного от этой точки на плоскость.

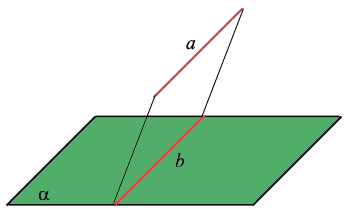
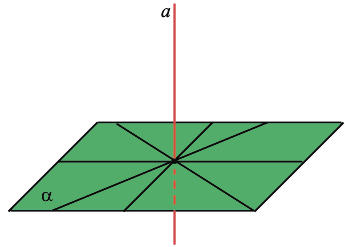
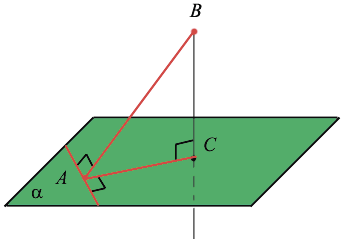
Наклонная, проведенная из данной точки к данной плоскости, — это любой отрезок, соединяющий данную точку с точкой плоскости, который не является перпендикуляром к плоскости. Конец отрезка, который лежит в плоскости, — это основание наклонной. Проекция наклонной — это отрезок, который соединяет основания перпендикуляра (точку С) и наклонной (точку А).

Если прямая, проведённая на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и наклонной. И обратно, если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

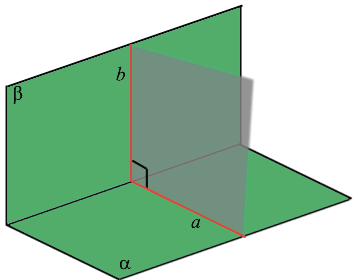
Две пересекающиеся плоскости называются перпендикулярными, если плоскость, перпендикулярная прямой их пересечения, пересекает данные плоскости по перпендикулярным прямым.

Так как , то .

Поделись с друзьями в социальных сетях:

Видео:№4. Точки А, В, С и D не лежат в одной плоскости, а) Могут ли какие-то три изСкачать

Параллельные прямые, признаки и условия параллельности прямых

В этой статье мы расскажем о параллельных прямых, дадим определения, обозначим признаки и условия параллельности. Для наглядности теоретического материала будем использовать иллюстрации и решение типовых примеров.

Видео:№12. Точки А, В, С, D не лежат в одной плоскости. Пересекаются ли плоскости, проходящие через точкиСкачать

Параллельные прямые: основные сведения

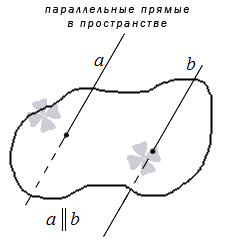
Параллельные прямые на плоскости – две прямые на плоскости, не имеющие общих точек.

Параллельные прямые в трехмерном пространстве – две прямые в трехмерном пространстве, лежащие в одной плоскости и не имеющие общих точек.

Необходимо обратить внимание, что для определения параллельных прямых в пространстве крайне важно уточнение «лежащие в одной плоскости»: две прямые в трехмерном пространстве, не имеющие общих точек и не лежащие в одной плоскости, являются не параллельными, а скрещивающимися.

Чтобы обозначить параллельность прямых, общепринято использовать символ ∥ . Т.е., если заданные прямые a и b параллельны, кратко записать это условие нужно так: a ‖ b . Словесно параллельность прямых обозначается следующим образом: прямые a и b параллельны, или прямая а параллельна прямой b , или прямая b параллельна прямой а .

Сформулируем утверждение, играющее важную роль в изучаемой теме.

Через точку, не принадлежащую заданной прямой проходит единственная прямая, параллельная заданной. Это утверждение невозможно доказать на базе известных аксиом планиметрии.

В случае, когда речь идет о пространстве, верна теорема:

Через любую точку пространства, не принадлежащую заданной прямой, будет проходить единственная прямая, параллельная заданной.

Эту теорему просто доказать на базе вышеуказанной аксиомы (программа геометрии 10 — 11 классов).

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Параллельность прямых: признаки и условия параллельности

Признак параллельности есть достаточное условие, при выполнении которого гарантирована параллельность прямых. Иначе говоря, выполнения этого условия достаточно, чтобы подтвердить факт параллельности.

В том числе, имеют место необходимые и достаточные условия параллельности прямых на плоскости и в пространстве. Поясним: необходимое – значит то условие, выполнение которого необходимо для параллельности прямых; если оно не выполнено – прямые не являются параллельными.

Резюмируя, необходимое и достаточное условие параллельности прямых – такое условие, соблюдение которого необходимо и достаточно, чтобы прямые были параллельны между собой. С одной стороны, это признак параллельности, с другой – свойство, присущее параллельным прямым.

Перед тем, как дать точную формулировку необходимого и достаточного условия, напомним еще несколько дополнительных понятий.

Секущая прямая – прямая, пересекающая каждую из двух заданных несовпадающих прямых.

Пересекая две прямые, секущая образует восемь неразвернутых углов. Чтобы сформулировать необходимое и достаточное условие, будем использовать такие типы углов, как накрест лежащие, соответственные и односторонние. Продемонстрируем их на иллюстрации:

Если две прямые на плоскости пересекаются секущей, то для параллельности заданных прямых необходимо и достаточно, чтобы накрест лежащие углы были равными, либо были равными соответственные углы, либо сумма односторонних углов была равна 180 градусам.

Проиллюстрируем графически необходимое и достаточное условие параллельности прямых на плоскости:

Доказательство указанных условий присутствует в программе геометрии за 7 — 9 классы.

В общем, эти условия применимы и для трехмерного пространства при том, что две прямые и секущая принадлежат одной плоскости.

Укажем еще несколько теорем, часто используемых при доказательстве факта параллельности прямых.

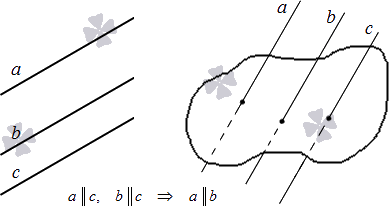
На плоскости две прямые, параллельные третьей, параллельны между собой. Этот признак доказывается на основе аксиомы параллельности, указанной выше.

В трехмерном пространстве две прямые, параллельные третьей, параллельны между собой.

Доказательство признака изучается в программе геометрии 10 класса.

Дадим иллюстрацию указанных теорем:

Укажем еще одну пару теорем, являющихся доказательством параллельности прямых.

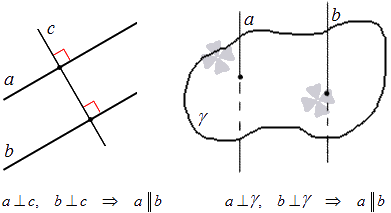
На плоскости две прямые, перпендикулярные третьей, параллельны между собой.

Сформулируем аналогичное для трехмерного пространства.

В трехмерном пространстве две прямые, перпендикулярные третьей, параллельны между собой.

Все указанные выше теоремы, признаки и условия позволяют удобно доказать параллельность прямых методами геометрии. Т.е., чтобы привести доказательство параллельности прямых, можно показать, что равны соответственные углы, или продемонстрировать факт, что две заданные прямые перпендикулярны третьей и т.д. Но отметим, что зачастую для доказательства параллельности прямых на плоскости или в трехмерном пространстве удобнее использовать метод координат.

Видео:№15. Три прямые попарно пересекаются. Докажите, что они либо лежат в одной плоскостиСкачать

Параллельность прямых в прямоугольной системе координат

В заданной прямоугольной системе координат прямая определяется уравнением прямой на плоскости одного из возможных видов. Так и прямой линии, заданной в прямоугольной системе координат в трехмерном пространстве, соответствуют некоторые уравнения прямой в пространстве.

Запишем необходимые и достаточные условия параллельности прямых в прямоугольной системе координат в зависимости от типа уравнения, описывающего заданные прямые.

Начнем с условия параллельности прямых на плоскости. Оно базируется на определениях направляющего вектора прямой и нормального вектора прямой на плоскости.

Чтобы на плоскости две несовпадающие прямые были параллельны, необходимо и достаточно, чтобы направляющие векторы заданных прямых были коллинеарными, или были коллинеарными нормальные векторы заданных прямых, или направляющий вектор одной прямой был перпендикулярен нормальному вектору другой прямой.

Становится очевидно, что условие параллельности прямых на плоскости базируется на условии коллинеарности векторов или условию перпендикулярности двух векторов. Т.е., если a → = ( a x , a y ) и b → = ( b x , b y ) являются направляющими векторами прямых a и b ;

и n b → = ( n b x , n b y ) являются нормальными векторами прямых a и b , то указанное выше необходимое и достаточное условие запишем так: a → = t · b → ⇔ a x = t · b x a y = t · b y или n a → = t · n b → ⇔ n a x = t · n b x n a y = t · n b y или a → , n b → = 0 ⇔ a x · n b x + a y · n b y = 0 , где t – некоторое действительное число. Координаты направляющих или прямых векторов определяются по заданным уравнениям прямых. Рассмотрим основные примеры.

1. Прямая a в прямоугольной системе координат определяется общим уравнением прямой: A 1 x + B 1 y + C 1 = 0 ; прямая b — A 2 x + B 2 y + C 2 = 0 . Тогда нормальные векторы заданных прямых будут иметь координаты ( А 1 , В 1 ) и ( А 2 , В 2 ) соответственно. Условие параллельности запишем так:

A 1 = t · A 2 B 1 = t · B 2

1. Прямая a описывается уравнением прямой с угловым коэффициентом вида y = k 1 x + b 1 . Прямая b — y = k 2 x + b 2 . Тогда нормальные векторы заданных прямых будут иметь координаты ( k 1 , — 1 ) и ( k 2 , — 1 ) соответственно, а условие параллельности запишем так:

k 1 = t · k 2 — 1 = t · ( — 1 ) ⇔ k 1 = t · k 2 t = 1 ⇔ k 1 = k 2

Таким образом, если параллельные прямые на плоскости в прямоугольной системе координат задаются уравнениями с угловыми коэффициентами, то угловые коэффициенты заданных прямых будут равны. И верно обратное утверждение: если несовпадающие прямые на плоскости в прямоугольной системе координат определяются уравнениями прямой с одинаковыми угловыми коэффициентами, то эти заданные прямые параллельны.

1. Прямые a и b в прямоугольной системе координат заданы каноническими уравнениями прямой на плоскости: x — x 1 a x = y — y 1 a y и x — x 2 b x = y — y 2 b y или параметрическими уравнениями прямой на плоскости: x = x 1 + λ · a x y = y 1 + λ · a y и x = x 2 + λ · b x y = y 2 + λ · b y .

Тогда направляющие векторы заданных прямых будут: a x , a y и b x , b y соответственно, а условие параллельности запишем так:

a x = t · b x a y = t · b y

Заданы две прямые: 2 x — 3 y + 1 = 0 и x 1 2 + y 5 = 1 . Необходимо определить, параллельны ли они.

Решение

Запишем уравнение прямой в отрезках в виде общего уравнения:

x 1 2 + y 5 = 1 ⇔ 2 x + 1 5 y — 1 = 0

Мы видим, что n a → = ( 2 , — 3 ) — нормальный вектор прямой 2 x — 3 y + 1 = 0 , а n b → = 2 , 1 5 — нормальный вектор прямой x 1 2 + y 5 = 1 .

Полученные векторы не являются коллинеарными, т.к. не существует такого значения t , при котором будет верно равенство:

2 = t · 2 — 3 = t · 1 5 ⇔ t = 1 — 3 = t · 1 5 ⇔ t = 1 — 3 = 1 5

Таким образом, не выполняется необходимое и достаточное условие параллельности прямых на плоскости, а значит заданные прямые не параллельны.

Ответ: заданные прямые не параллельны.

Заданы прямые y = 2 x + 1 и x 1 = y — 4 2 . Параллельны ли они?

Решение

Преобразуем каноническое уравнение прямой x 1 = y — 4 2 к уравнению прямой с угловым коэффициентом:

x 1 = y — 4 2 ⇔ 1 · ( y — 4 ) = 2 x ⇔ y = 2 x + 4

Мы видим, что уравнения прямых y = 2 x + 1 и y = 2 x + 4 не являются одинаковыми (если бы было иначе, прямые были бы совпадающими) и угловые коэффициенты прямых равны, а значит заданные прямые являются параллельными.

Попробуем решить задачу иначе. Сначала проверим, совпадают ли заданные прямые. Используем любую точку прямой y = 2 x + 1 , например, ( 0 , 1 ) , координаты этой точки не отвечают уравнению прямой x 1 = y — 4 2 , а значит прямые не совпадают.

Следующим шагом определим выполнение условия параллельности заданных прямых.

Нормальный вектор прямой y = 2 x + 1 это вектор n a → = ( 2 , — 1 ) , а направляющий вектором второй заданной прямой является b → = ( 1 , 2 ) . Скалярное произведение этих векторов равно нулю:

n a → , b → = 2 · 1 + ( — 1 ) · 2 = 0

Таким образом, векторы перпендикулярны: это демонстрирует нам выполнение необходимого и достаточного условия параллельности исходных прямых. Т.е. заданные прямые параллельны.

Ответ: данные прямые параллельны.

Для доказательства параллельности прямых в прямоугольной системе координат трехмерного пространства используется следующее необходимое и достаточное условие.

Чтобы две несовпадающие прямые в трехмерном пространстве были параллельны, необходимо и достаточно, чтобы направляюще векторы этих прямых были коллинеарными.

Т.е. при заданных уравнениях прямых в трехмерном пространстве ответ на вопрос: параллельны они или нет, находится при помощи определения координат направляющих векторов заданных прямых, а также проверки условия их коллинеарности. Иначе говоря, если a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) являются направляющими векторами прямых a и b соответственно, то для того, чтобы они были параллельны, необходимо существование такого действительного числа t , чтобы выполнялось равенство:

a → = t · b → ⇔ a x = t · b x a y = t · b y a z = t · b z

Заданы прямые x 1 = y — 2 0 = z + 1 — 3 и x = 2 + 2 λ y = 1 z = — 3 — 6 λ . Необходимо доказать параллельность этих прямых.

Решение

Условиями задачи заданы канонические уравнения одной прямой в пространстве и параметрические уравнения другой прямой в пространстве. Направляющие векторы a → и b → заданных прямых имеют координаты: ( 1 , 0 , — 3 ) и ( 2 , 0 , — 6 ) .

1 = t · 2 0 = t · 0 — 3 = t · — 6 ⇔ t = 1 2 , то a → = 1 2 · b → .

Следовательно, необходимое и достаточное условие параллельности прямых в пространстве выполнено.

Ответ: параллельность заданных прямых доказана.

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Введение в стереометрию. Параллельность

Важные аксиомы стереометрии

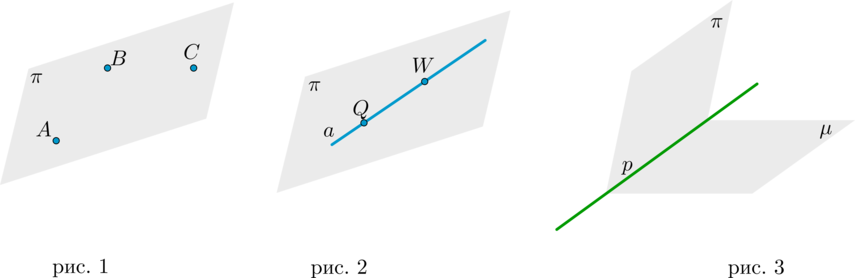
1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Таким образом, любая плоскость однозначно задается тремя точками, не лежащими на одной прямой: (pi=(ABC)) (рис. 1).

2. Если две точки прямой лежат в некоторой плоскости, то и вся прямая лежит в этой плоскости: (ain pi) .
Говорят также, что плоскость содержит прямую: (pisubset a) (рис. 2).

3. Если две плоскости имеют общую точку, то они имеют и общую прямую, на которой лежат все общие точки этих плоскостей.
Таким образом, если плоскости пересекаются, то они пересекаются по прямой: (picap mu=p) .
Данная прямая (p) называется линией пересечения плоскостей (рис. 3).

Заметим, что плоскость обычно изображают в виде внутренности параллелограмма. Почему? Посмотрите, например, сбоку на стол. В виде какой фигуры выглядит столешница?

Следствия из аксиом

1. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна (рис. 4).

2. Через две пересекающиеся прямые проходит плоскость, и притом только одна (рис. 5).

Доказательство

1. Действительно, отметим на прямой (a) некоторые две точки (A) и (B) . Тогда мы получим три точки (A, B, C) , не лежащие на одной прямой. Через них можно провести единственную плоскость (pi) . А т.к. две выбранные точки (A) и (B) прямой лежат в этой плоскости, то и вся прямая лежит в этой плоскости.

2. Действительно, пусть (O) – точка пересечения данных прямых (p) и (q) . Отметим еще по одной точке (P) и (Q) на каждой прямой (отличающиеся от точки (O) ). Получили три точки (P, Q, O) , не лежащие на одной прямой. Через них проходит единственная плоскость (pi) . А т.к. две точки каждой прямой лежат в этой плоскости, то и все точки каждой прямой будут лежать в этой плоскости.

Определения

Две прямые в пространстве параллельны, если они лежат в одной плоскости и не пересекаются.

Следствие 1

Через две параллельные прямые проходит плоскость, и притом только одна.

Теорема 1

Через любую точку (A) в пространстве, не лежащую на данной прямой (b) , проходит прямая (a) , параллельная данной, и притом только одна.

Доказательство

Через точку (A) и прямую (b) можно провести единственную плоскость (по аксиоме); пусть эта плоскость называется (pi) . Прямая (a) , параллельная прямой (b) , должна лежать с ней в одной плоскости, а также должна проходить через точку (A) , следовательно, должна лежать в плоскости (pi) . Но в плоскости через точку, не лежащую на прямой, можно провести ровно одну прямую, параллельную данной (теорема планиметрии), чтд.

Теорема 2

Если одна из двух параллельных прямых пересекает плоскость, то и другая прямая пересекает эту плоскость.

Доказательство

Пусть (aparallel b) и (acap pi=A) . Докажем, что и (b) пересечет плоскость (pi) (назовем их точку пересечения (B) ).

Проведем через прямые (a) и (b) плоскость (mu) (это возможно в силу определения параллельных прямых). Тогда плоскости (pi) и (mu) имеют общую точку (A) , следовательно, имеют и общую прямую (p) , на которой лежат все их общие точки. Но т.к. (bparallel a) и (acap p=A) , то прямая (b) тоже пересекает прямую (p) . Значит, прямая (b) пересекает и плоскость (mu) (это и есть точка (B) ).

Теорема 3: о параллельности трех прямых

Если прямая (a) параллельна прямой (b) , а та в свою очередь параллельна прямой (c) , то (aparallel c) .

Доказательство

1) Отметим некоторую точку (C) на прямой (c) и проведем плоскость (pi) через прямую (a) и точку (C) . Прямая (c) будет лежать в этой плоскости. Действительно, т.к. прямая (c) и плоскость (pi) имеют общую точку (C) , то в противном случае прямая (c) будет пересекать эту плоскость. Но т.к. (bparallel c) , то и прямая (b) будет пересекать (pi) ; а т.к. (aparallel b) , то и прямая (a) будет пересекать эту плоскость. А это противоречит нашему построению.

2) Теперь прямые (a) и (c) лежат в одной плоскости, значит, они могут либо пересекаться, либо быть параллельны. Предположим, что (c) пересекает (a) в точке (A) . Тогда получается, что через точку (A) проведены две прямые, параллельные прямой (b) , что противоречит теореме 1.

Определение

Существует три вида взаимного расположения прямой и плоскости:

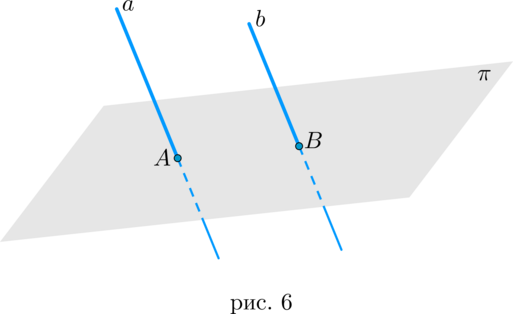
1. прямая имеет с плоскостью две общие точки (то есть лежит в плоскости) — рис. 4;

2. прямая имеет с плоскостью ровно одну общую точку (то есть пересекает плоскость) — рис. 6;

3. прямая не имеет с плоскостью общих точек (то есть параллельна плоскости).

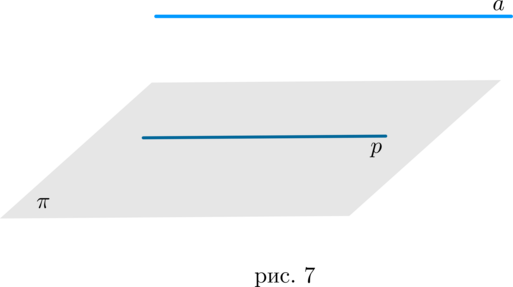
Теорема 4: признак параллельности прямой и плоскости

Если прямая (a) , не лежащая в плоскости (pi) , параллельна некоторой прямой (p) , лежащей в плоскости (pi) , то она параллельна данной плоскости (рис. 7).

Доказательство

Докажем, что прямая (a) не может пересекать плоскость (pi) (случай, что прямая лежит в плоскости, невозможен по условию). Предположим, что это не так. Во-первых, проведем плоскость (mu) через прямые (a) и (p) (значит, плоскости (pi) и (mu) пересекаются по прямой (p) ). Во-вторых, пусть (acappi=A) . Т.к. (aparallel p) , то точка (A) не может лежать на прямой (p) . Значит, плоскости (pi) и (mu) имеют еще одну общую точку (A) , не лежащую на их линии пересечения, что противоречит аксиоме 3. Чтд.

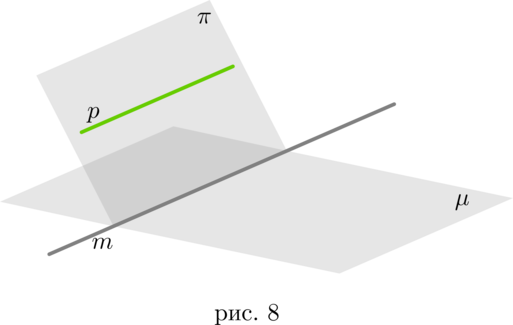
Следствие 2

Пусть прямая (p) параллельна плоскости (mu) . Если плоскость (pi) проходит через прямую (p) и пересекает плоскость (mu) , то линия пересечения плоскостей (pi) и (mu) — прямая (m) — параллельна прямой (p) (рис. 8).

Доказательство

Т.к. прямые (m) и (p) лежат в одной плоскости (pi) , то они могут быть либо параллельны, либо пересекаться, либо совпадать. Совпадать они не могут, потому что тогда (pin mu) , а это противоречит условию. Если (mcap p=O) , то (p) пересекает плоскость (mu) в точке (O) , что опять же противоречит условию. Значит, (mparallel p) .

Следствие 3

Если прямые (a) и (b) параллельны и прямая (a) также параллельна плоскости (alpha) , то и прямая (b) либо параллельна, либо лежит в плоскости (alpha) .

Определение

Существует три типа взаимного расположения плоскостей в пространстве: совпадают (имеют три общие точки, не лежащие на одной прямой), пересекаются (имеют общие точки, лежащие строго на одной прямой), и не имеют общих точек.

Если две плоскости не имеют общих точек, то они называются параллельными плоскостями.

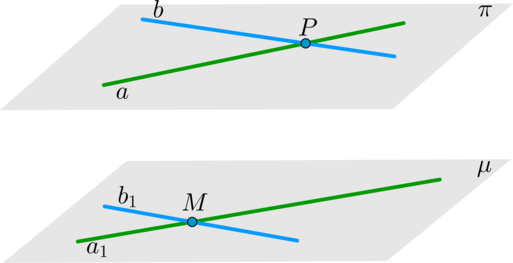
Теорема 5: признак параллельности плоскостей

Если две пересекающиеся прямых из одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости будут параллельны.

Доказательство

Рассмотрим две плоскости (pi) и (mu) и в них пересекающиеся прямые (a, b) и (a_1, b_1) соответственно, такие что (aparallel a_1, bparallel b_1) . Докажем, что плоскости не имеют общих точек.

Предположим, что это не так. Пусть плоскости имеют общую точку, значит они имеют и общую прямую (y) : (picap mu=y) . Данная прямая не может быть параллельна обеим прямым (a) и (b) (т.к. они все лежат в одной плоскости (pi) ), значит, хотя бы одну из этих прямых она пересекает. Пусть это будет прямая (a) , то есть (acap y=Y) . Т.к. прямая (y) лежит и в плоскости (mu) , то (Yin mu) , то есть прямая (a) имеет с плоскостью (mu) общую точку (Y) . Но это невозможно, т.к. по признаку параллельности прямой и плоскости прямая (a) параллельна плоскости (mu) . Чтд.

Следствие 4

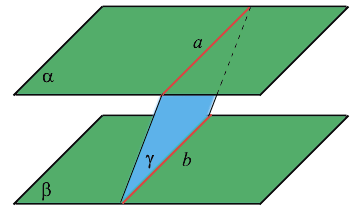
Если две параллельные плоскости (alpha) и (beta) пересечены третьей плоскостью (gamma) , то линии пересечения плоскостей также параллельны:

[alphaparallel beta, alphacap gamma=a, betacapgamma=b Longrightarrow aparallel b]

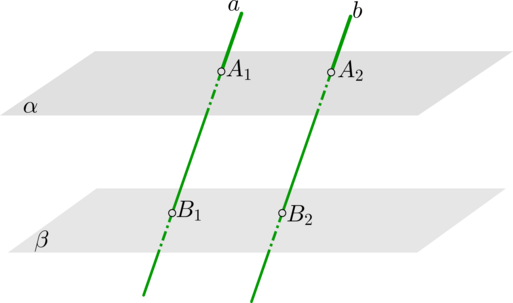
Следствие 5

Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны:

[alphaparallel beta, aparallel b Longrightarrow A_1B_1=A_2B_2]

📺 Видео

Параллельные прямые | Математика | TutorOnlineСкачать

№16. Параллельные прямые a и b лежат в плоскости α. Докажите,Скачать

№3. Верно ли, что: а) любые три точки лежат в одной плоскости;Скачать

Как проверить лежат ли 4 точки в одной плоскости Аналитическая геометрияСкачать

10 класс, 7 урок, Скрещивающиеся прямыеСкачать

№7. Две прямые пересекаются в точке М. Докажите, что все прямые, не проходящие через точкуСкачать

№64. Три прямые, проходящие через одну точку и не лежащие в одной плоскости, пересекают однСкачать

№11. Даны прямая и точка, не лежащая на этой прямой. Докажите, что все прямые, проходящие черезСкачать

№41. Может ли каждая из двух скрещивающихся прямых быть параллельна третьей прямойСкачать

Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Параллельность прямых. 10 класс.Скачать

Параллельность прямых. Практическая часть. 10 класс.Скачать

10 класс, 3 урок, Некоторые следствия из аксиомСкачать

10.2 Параллельность прямых, прямой и плоскостиСкачать