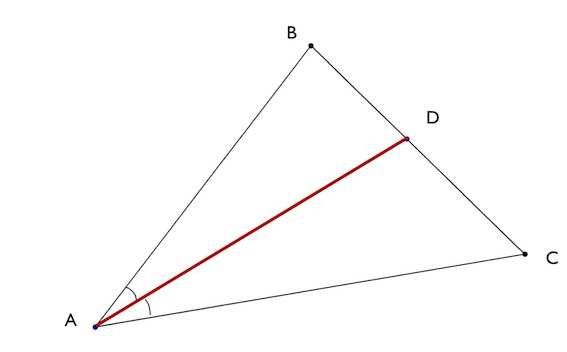
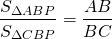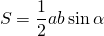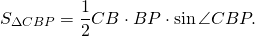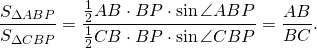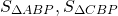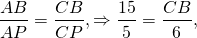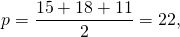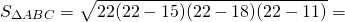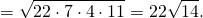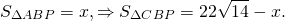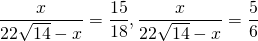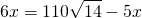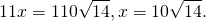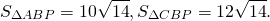Биссектриса и площадь треугольника

Биссектриса треугольника – отрезок биссектрисы угла треугольника, заключенный между вершиной треугольника и противолежащей ей стороной.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Свойства биссектрисы

1. Биссектриса треугольника делит угол пополам.

2. Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон ()

3. Точки биссектрисы угла треугольника равноудалены от сторон этого угла.

4. Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности.

Видео:Биссектриса и площадь треугольника.Скачать

Некоторые формулы, связанные с биссектрисой треугольника

(доказательство формулы – здесь)
, где
— длина биссектрисы, проведённой к стороне ,
— стороны треугольника против вершин соответственно,
— длины отрезков, на которые биссектриса делит сторону ,

Приглашаю посмотреть видеоурок, в котором демонстрируется применение всех указанных выше свойств биссектрисы.

Задачи, рассматриваемые в видеоролике:
1.В треугольнике АВС со сторонами АВ=2 см, ВС=3 см, АС=3 см проведена биссектриса ВМ. Найти длины отрезков АМ и МС
2. Биссектриса внутреннего угла при вершине А и биссектриса внешнего угла при вершине С треугольника АВС пересекаются в точке М. Найдите угол BMC, если угол В равен 40, угол С – 80 градусов
3. Найти радиус окружности, вписанной в треугольник, считая стороны квадратных клеток равными 1

Возможно, вам будет интересен и этот небольшой видеоурок, где применяется одно из свойств биссектрисы

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Видео:Свойство биссектрисы треугольника с доказательствомСкачать

Биссектриса делит площадь

Биссектриса делит площадь треугольника пропорционально прилежащим сторонам.

Дано : ∆ABC,

Площадь треугольника равна половине произведения сторон на синус угла между ними

Так как BP — биссектриса треугольника ABC, то ∠ABP=∠CBP, отсуда sin∠ABP=sin∠CBP.

Что и требовалось доказать .

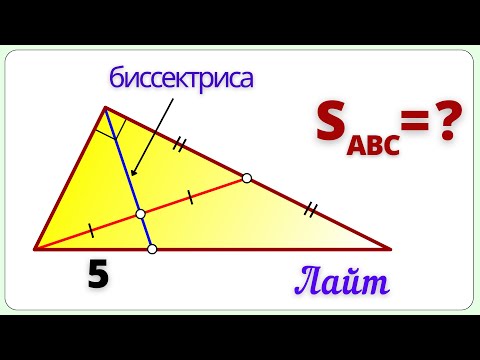
Биссектриса треугольника делит противоположную сторону на части 5 и 6. Меньшая из двух других сторон равна 15. Найти площади частей, на которые биссектриса делит исходный треугольник.

Дано : ∆ABC,

BP — биссектриса, AP=5, CP=6, AB=15

откуда BC=18. AC=AP+CP=11.

Площадь треугольника ABC найдём по формуле Герона.

Так как биссектриса делит площадь треугольника на части, пропорциональные прилежащим сторонам,

Ответ: 10√14 и 12√14.

Видео:Секретные формулы биссектрисы треугольника!😉❤️‍🔥#математика #егэСкачать

3 Comments

Биссектриса угла треугольника делит его сторону наотрезки, разность которых 3см, две другие стороны 14см и 21см. Вычислить площадь треугольника.

Пусть один из отрезков равен x см, тогда другой — (x+3) см. По свойству биссектрисы треугольника 14:21=x:(x+3). Отсюда x=6, x+3=9, то есть длина третьей стороны треугольника 6+9=15 см. Зная все три стороны треугольника, площадь можем найти по формуле Герона.

Видео:Биссектриса прямого угла делит медиану пополам! Найти площадь треугольника.Скачать

Геометрия. Урок 3. Треугольники

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

• Определение треугольника

• Виды треугольников

• Отрезки в треугольнике

Видео:Формула для биссектрисы треугольникаСкачать

Определение треугольника

Треугольник – многоугольник с тремя сторонами и тремя углами.

Угол ∠ A – угол, образованный сторонами A B и A C и противолежащий стороне B C .

Угол ∠ B – угол, образованный сторонами B A и B C и противолежащий стороне A C .

Угол ∠ C – угол, образованный сторонами C B и C A и противолежащий стороне A B .

Видео:Как найти длину биссектрисы, медианы и высоты? | Ботай со мной #031 | Борис ТрушинСкачать

Виды треугольников

Треугольник остроугольный , если все три угла в треугольнике острые.

Треугольник прямоугольный , если у него один из углов прямой ( = 90 ° ) .

Треугольник тупоугольный , если у него один из углов тупой.

Основные свойства треугольника:

• Против большей стороны лежит больший угол.
• Против равных сторон лежат равные углы.
• Сумма углов в треугольнике равна 180 ° .
• Если продолжить одну из сторон треугольника, например, A C , и взять на продолжении стороны точку D , образуется внешний угол ∠ B C D к исходному углу ∠ A C B .

Видео:Длины биссектрис и площадь треугольникаСкачать

Отрезки в треугольнике

Биссектриса угла – луч, выходящий из вершины угла и делящий его пополам.

Биссектриса треугольника – отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне.

Свойства биссектрис треугольника:

• Биссектриса угла – геометрическое место точек, равноудаленных от сторон угла.
• Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам:

Замечание: биссектриса угла – это луч, а биссектриса треугольника – отрезок.

Медиана треугольника – отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.

Свойства медиан треугольника:

• Медиана разбивает треугольник на два равновеликих треугольника (два треугольника, имеющих одинаковую площадь).
• Медианы треугольника пересекаются в одной точке. Точка пересечения медиан делит их в отношении 2:1, считая от вершины.

Высота треугольника – это перпендикуляр, проведенный из вершины угла треугольника к прямой, содержащей противолежащую сторону этого треугольника.

Если треугольник остроугольный, то все три высоты будут лежать внутри треугольника. Если треугольник тупоугольный, то высоты, проведенные из вершин острых углов будут лежать вне треугольника, а высота, проведенная из вершины тупого угла будет лежать внутри треугольника.

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Свойство средней линии треугольника: средняя линия параллельна одной из его сторон и равна половине этой стороны.

Всего в треугольнике можно провести три средние линии. Три средние линии разбивают исходный треугольник на четыре равных треугольника. Площадь каждого маленького треугольника будет равна четверти площади большого треугольника.

Видео:№535. Докажите, что биссектриса треугольника делит противоположную сторону на отрезки,Скачать

Площадь треугольника

Площадь произвольного треугольника можно найти следующими способами:

Полупроизведение стороны на высоту, проведенную к этой стороне.

Видео:ВЫСОТА ТРЕУГОЛЬНИКА 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Равнобедренный треугольник

Равнобедренным называется треугольник, у которого две стороны равны.

Равнобедренный треугольник может быть остроугольным, прямоугольным и тупоугольным.

Свойства равноберенного треугольника:

• В равнобедренном треугольнике углы при основании равны.
• В равнобедренном треугольнике медиана, высота и биссектриса, проведенные к основанию, совпадают.

Видео:Как найти биссектрису в треугольнике? 2 формулы биссектрисыСкачать

Равносторонний треугольник

Равносторонним называется треугольник, у которого все стороны и все углы равны.

Площадь равностороннего треугольника находится по формуле S = a 2 3 4

Высота равностороннего треугольника находится по формуле h = a 3 2

Видео:Запомни: все формулы для площади треугольникаСкачать

Прямоугольный треугольник

Треугольник называется прямоугольным, если у него один из углов равен 90 ° .

Свойства прямоугольного треугольника:

• Сумма двух острых углов треугольника равна 90 ° .
• Катет, лежащий напротив угла в 30 ° , равен половине гипотенузы.
• Если катет равен половине гипотенузы, он лежит напротив угла в 30 ° .

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Теорема Пифагора

Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.

У прямоугольного треугольника катеты перпендикулярны друг другу, следовательно, площадь можно найти по формуле:

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с треугольниками

🔥 Видео

ЕГЭ 2024 по математике. №1,17 Медиана, биссектриса, высота, серединный перпендикулярСкачать

Длина биссектрисы треугольникаСкачать

Формулы равностороннего треугольника #shortsСкачать

Геометрия Площадь треугольника ABC равна 80. Биссектриса AD пересекает медиану BK в точке E, приСкачать

Свойства биссектрисыСкачать

Свойство биссектрисы треугольникаСкачать