Основные метрические сооьтношения в прямоугольном треугольнике
§1. Прямоугольный треугольник. Метрические соотношения.
Основные метрические сооьтношения в прямоугольном треугольнике
Пусть `ABC` прямоугольный треугольник с прямым углом `C` и острым углом при вершине `A`, равным `alpha` (рис. 1).
Используем обычные обозначения:
`c` — гипотенуза `AB`;
`a` и `b` – катеты `BC` и `AC` (по-гречески «kathetos — катет» означает отвес, поэтому такое изображение прямоугольного треугольника нам представляется естественным);
`a_c` и `b_c` – проекции `BD` и `AD` катетов на гипотенузу;
`h` – высота `CD`, опущенная на гипотенузу;
`m_c` – медиана `CM`, проведённая к гипотенузе;
`R` – радиус описанной окружности;
`r` – радиус вписанной окружности.
Напомним, что если `alpha` — величина острого угла `A` прямоугольного треугольника `ABC` (см. рис. 1), то
`sin alpha = a/c`, `cos alpha = b/c` и `»tg»alpha = a/b`.
Значения синуса, косинуса и тангенса острого угла прямоугольного треугольника зависят только от меры угла и не зависят от размеров и расположения треугольника.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
`c^2 = a^2 + b^2`
Доказательство теоремы повторите по учебнику.
Выведем ряд соотношений между элементами прямоугольного треугольника.
Квадрат катета равен произведению гипотенузы и его проекции на гипотенузу
Если `/_ A = alpha` (см. рис. 1), то `/_ CBD = 90^@ — alpha` и `/_ BCD = alpha`. Из треугольника `ABC` `sin alpha = (BC)/(AB)`, а из треугольника `BCD` `sin alpha = (BD)/(BC)`.
Значит, `(BC)/(AB) = (BD)/(BC)`, откуда `BC^2 = AB * BD`, т. е. `a^2 = c * a_c` . Аналогично доказывается второе равенство.
Квадрат высоты, опущенной на гипотенузу, равен произведению проекции катетов на гипотенузу
Из треугольника `ACD` (рис. 1) имеем `»tg»alpha = (CD)/(AD)`, а из треугольника `BCD` `»tg»alpha = (BD)/(CD)`.
Значит `(BD)/(CD) = (CD)/(AD)`, откуда `CD^2 = AD * BD`, т. е. `h^2 = a_c * b_c`.
Произведение катетов равно произведению гипотенузы и высоты, опущенной на гипотенузу
Из треугольника `ABC` имеем `sin alpha = (BC)/(AB)`, а из треуольника `ACD` `sin alpha = (CD)/(AC)`.
Таким образом, `(BC)/(AB) = (CD)/(AC)`, откуда `BC * AC = AB * CD`, т. е. `a * b = c * h`.
Медиана, проведённая к гипотенузе, равна половине гипотенузы, т. е.
Пусть `AM = BM`. Проведём $$ MKVert BC$$ (рис. 2), тогда по теореме Фалеса `AK = CK`
.
Кроме того, из того, что `BC _|_ AC` и $$ MKVert BC$$ следует `MK _|_ AC`. В прямоугольных треугольниках `CMK` и `AMK` катет `MK` общий, катеты `CK` и `AK` равны. Эти треугольники равны и `CM = AM`, т. е. `CM = 1/2 AB`.
Полезно также запомнить, что медиана к гипотенузе разбивает треугольник на два равнобедренных треугольника.
Радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы
Это следует из Свойства 4, действительно, `MA = MB = MC`, следовательно, окружность с центром в точке `M` и радиуса `c/2` проходит через три вершины.
Сумма катетов равна удвоенной сумме радиусов описанной и вписанной окружностей
`a + b = 2(R + r)` или `a + b = c + 2r`
Пусть `O` — центр вписанной окружности и `F`, `N` и `S` — точки касания сторон треугольника `ABC` (рис. 3), тогда `OF_|_ BC`, `ON _|_ AC`, `OS _|_ AB` и `OF = ON = OS = r`. Далее, `OFCN` — квадрат со стороной `r`, поэтому `BF = BC — FC`, `AN = AC — CN`, т. е. `BF = a — r` и `AN = b — r`.
Прямоугольные треугольники `AON` и `AOS` равны (гипотенуза `AO` — общая, катеты `ON` и `OS` равны), следовательно, `AS = AN`, т. е. `AS = b — r`.
Аналогично доказывается, что `BS = a — r`, поэтому из `AB = AS + BS` следует `c = (b — r) + (a — r)`, т. е. `a + b = c + 2r`. Зная, что `c = 2R`, окончательно получаем `a + b = 2(R + r)`.
Равенства, доказанные в Свойствах 1 и 2, записываются также как:
Видео:Математика | Метрические соотношения в прямоугольном треугольникеСкачать

Метрические соотношения в треугольника
§ 16. Теорема Пифагора.
§ 17. Тригонометрические функции острого угла прямоугольного треугольника.
§ 18. Решение прямоугольных треугольников.
ИТОГИ ГЛАВЫ 3
Метрические соотношения в прямоугольном треугольнике
Квадрат высоты прямоугольного треугольника, проведённой к гипотенузе, равен произведению проекций катетов на гипотенузу. Квадрат катета равен произведению гипотенузы и проекции этого катета на гипотенузу.
Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Синус острого угла прямоугольного треугольника
Синусом острого угла прямоугольного треугольника называют отношение противолежащего катета к гипотенузе.
Косинус острого угла прямоугольного треугольника
Косинусом острого угла прямоугольного треугольника называют отношение прилежащего катета к гипотенузе.
Тангенс острого угла прямоугольного треугольника
Тангенсом острого угла прямоугольного треугольника называют отношение противолежащего катета к прилежащему.
Котангенс острого угла прямоугольного треугольника
Котангенсом острого угла прямоугольного треугольника называют отношение прилежащего катета к противолежащему.
Тригонометрические формулы
Соотношения между сторонами и значениями тригонометрических функций углов в прямоугольном треугольнике
- Катет прямоугольного треугольника равен произведению гипотенузы на синус угла, противолежащего этому катету.
- Катет прямоугольного треугольника равен произведению гипотенузы на косинус угла, прилежащего к этому катету.
- Катет прямоугольного треугольника равен произведению второго катета на тангенс угла, противолежащего первому катету.
- Катет прямоугольного треугольника равен произведению второго катета на котангенс угла, прилежащего к первому катету.
- Гипотенуза прямоугольного треугольника равна частному от деления катета на синус противолежащего ему угла.
- Гипотенуза прямоугольного треугольника равна частному от деления катета на косинус прилежащего к нему угла.
«Мерзляк Геометрия 8 Глава 3» СОДЕРЖАНИЕ: § 15. Метрические соотношения в прямоугольном треугольнике. § 16. Теорема Пифагора. § 17. Тригонометрические функции острого угла прямоугольного треугольника. § 18. Решение прямоугольных треугольников.
Это конспект по теме «Мерзляк Геометрия 8 Глава 3». Выберите дальнейшие действия: Вернуться к Списку конспектов по геометрии.
Видео:МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ . §15 геометрия 8 классСкачать

Метрические соотношения в треугольнике.
Соотношения между сторонами и углами треугольника.
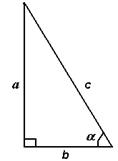 | 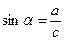 | В прямоугольном треугольнике синус угла равен отношению противолежащего катета к гипотенузе. |
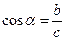 | В прямоугольном треугольнике косинус угла равен отношению прилежащего катета к гипотенузе. | |
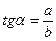 | В прямоугольном треугольнике тангенс угла равен отношению противолежащего катета к прилежащему. | |
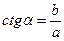 | В прямоугольном треугольнике котангенс угла равен отношению прилежащего катета к противолежащему. |
Теорема 24. (Пифагора) В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Теорема 25. (Теорема, обратная теореме Пифагора) Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
С помощью теоремы, обратной к теореме Пифагора, можно по длинам сторон определить, является он прямоугольным или нет.
Наиболее интересны прямоугольные треугольники с целочисленными длинами сторон. Так, например, треугольники
3, 4, 5 и далее им подобные 6, 8, 10, далее 9, 12, 15 и т.д.
5, 12, 13 и далее им подобные 10, 24, 26 и т.д.
8, 15, 17 и далее им подобные.
7, 24, 25 и далее им подобные.
Скорее всего таких независимых серий прямоугольных треугольников с целочисленными длинами сторон бесконечно много.
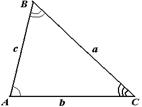 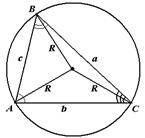 | Теорема 26. (синусов) Стороны треугольника пропорциональны синусам противолежащих углов. 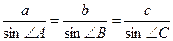 . Следствием к теореме синусов можно считать следующую теорему. Теорема 27. Стороны треугольника пропорциональны синусам противолежащих углов и их отношения равны двум радиусам описанной окружности около данного треугольника.. . Следствием к теореме синусов можно считать следующую теорему. Теорема 27. Стороны треугольника пропорциональны синусам противолежащих углов и их отношения равны двум радиусам описанной окружности около данного треугольника.. 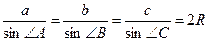 . . |
 | Теорема 28. (косинусов) Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними. 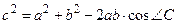 . . |
Дата добавления: 2014-12-22 ; просмотров: 7327 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
🔥 Видео
Метрические соотношения в прямоугольном треугольнике. 1 часть. 9 класс.Скачать

Метрические соотношения в прямоугольном треугольнике - геометрия 8 классСкачать

Метрические соотношения в треугольнике. ГеометрияСкачать

Метрические соотношения в прямоугольном треугольнике. 2 часть. 9 класс.Скачать

8 класс Геометрия. Метрические соотношения в прямоугольном треугольнике. Высота к гипотенузе Урок #7Скачать

Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

29. Метрические соотношения в прямоугольном треугольникеСкачать

Прикладная задача по геометрии. Метрические соотношения в треугольнике.Скачать

Математика, 10-й класс, Метрические соотношения в треугольнике. Теорема синусовСкачать

2017-02-13 Геометрия 8 класс. Метрические соотношения в прямоугольном треугольникеСкачать

Соотношения между сторонами и углами треугольника. 7 класс.Скачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Метрические соотношения в треугольнике. Диафильм по математике для 8-го классаСкачать

Метрические соотношения в прямоугольном треугольнике. Соотношение 2.Скачать

Метрические соотношения в прямоугольном треугольникеСкачать

Прямоугольный треугольник. Метрические соотношения.Скачать

Геометрия, 9 класс | Метрические соотношения в окружностиСкачать















