Найдите радиус окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно
Это задание ещё не решено, приводим решение прототипа.
Найдите радиус окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (−2; −2), (6; −2), (6; 4), (−2; 4).
Диагональ прямоугольника образует два прямоугольных треугольника. Диагональ равна диаметру окружности, описанной около треугольника. По формуле вычисления длины отрезка, заданного координатами концов, находим:
По теореме Пифагора находим, что Поэтому
- Прямоугольник. Онлайн калькулятор
- Свойства прямоугольника
- Диагональ прямоугольника
- Окружность, описанная около прямоугольника
- Формула радиуса окружности описанной около прямоугольника
- Периметр прямоугольника
- Формулы сторон прямоугольника через его диагональ и периметр
- Признаки прямоугольника
- «решение заданий В-3» егэ
- Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
- Описание презентации по отдельным слайдам:
- Охрана труда
- Библиотечно-библиографические и информационные знания в педагогическом процессе
- Охрана труда
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- 🔥 Видео
Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

Прямоугольник. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ прямоугольника, радиус описанной вокруг прямоугольника окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Определение 1. Прямоугольник − это параллелограмм, у которого все углы прямые (Рис.1).
 |
Можно дать и другое определение прямоугольника.
Определение 2. Прямоугольник − это четырехугольник, у которого все углы прямые.
Видео:Задание 3 ЕГЭ по математике. Урок 70Скачать

Свойства прямоугольника
Так как прямоугольник является параллелограммом, то все свойства параллелограмма верны и для прямоугольника.
- 1. Стороны прямоугольника являются его высотами.
- 2. Все углы прямоугольника прямые.
- 3. Квадрат диагонали прямоугольника равен сумме квадратов его соседних двух сторон.
- 4. Диагонали прямоугольника равны.
- 5. Около любого прямоугольника можно описать окружность, при этом диаметр описанной окружности равна диагонали прямоугольника.
Длиной прямоугольника называется более длинная пара его сторон.
Шириной прямоугольника называется более короткая пара его сторон.
Видео:2047 радиус окружности описанной около правильного треугольника равна 36 корней из 3Скачать

Диагональ прямоугольника
Определение 3. Диагональ прямоугольника − это отрезок, соединяющий две несмежные вершины прямоугольника.
 |
На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. Прямоугольник имеет две диагонали.
Для вычисления длины диагонали воспользуемся теоремой Пифагора:
 |
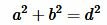 . . | (1) |
Из равенства (1) найдем d:
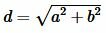 . . | (2) |
Пример 1. Стороны прямоугольника равны 
Решение. Для нахождения диаметра прямоугольника воспользуемся формулой (2). Подставляя 
 |
Ответ:
Видео:Геометрия Радиус окружности описанной около треугольника ABC равен 6 см Найдите радиус окружностиСкачать

Окружность, описанная около прямоугольника
Определение 4. Окружность называется описанной около прямоугольника, если все вершины прямоугольника находятся на этой окружности (Рис.3):
 |
Видео:Геометрия Найти радиус окружности, описанной около прямоугольного треугольника, если радиусСкачать

Формула радиуса окружности описанной около прямоугольника
Выведем формулу вычисления радиуса окружности, описанной около прямоугольника через стороны прямоугольника.
Нетрудно заметить, что радиус описанной около прямоугольника окружности равна половине диагонали (Рис.3). То есть
| ( small R=frac ) | (3) |
Подставляя (3) в (2), получим:
| ( small R=frac<large sqrt> ) | (4) |
Пример 2. Стороны прямоугольника равны 
Решение. Для нахождения радиуса окружности описанной вокруг прямоугольника воспользуемся формулой (4). Подставляя 
 |
 |
Ответ:
Видео:Задание 16 ОГЭ по математике. Окружность описана около квадратаСкачать

Периметр прямоугольника
Определение 5. Периметр прямоугольника − это сумма всех его сторон. Обозначается периметр латинской буквой P.
Периметр прямоугольника вычисляется формулой:
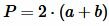 | (5) |
где ( small a ) и ( small b ) − стороны прямоугольника.
Пример 3. Стороны прямоугольника равны 
Решение. Для нахождения периметра прямоугольника воспользуемся формулой (5). Подставляя 
 |
Ответ:
Видео:Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать

Формулы сторон прямоугольника через его диагональ и периметр
Выведем формулу вычисления сторон прямоугольника, если известны диагональ ( small d ) и периметр ( small P ) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие ( small frac P2>d ) (это следует из неравенства треугольника).
Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:
 | (6) |
 | (7) |
Из формулы (7) найдем ( small b ) и подставим в (6):
 | (8) |
 | (9) |
Упростив (4), получим квадратное уравнение относительно неизвестной ( small a ):
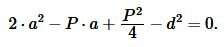 | (10) |
Вычислим дискриминант квадратного уравнения (10):
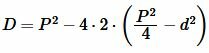 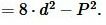 | (11) |
Сторона прямоугольника вычисляется из следующих формул:
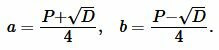 | (12) |
После вычисления ( small a ), сторона ( small b ) вычисляется или из формулы (12), или из (8).
Примечание. Легко можно доказать, что
| ( frac >d ; ⇒ ; P>2cdot d ; ⇒ ) ( small P^2>4 cdot d^2 ; ⇒ ; 4d^2-P^2 2d .) Следовательно выполняется неравенство (*). |
Пример 4. Диагональ прямоугольника равна 

Решение. Для нахождения сторон прямоугольника воспользуемся формулами (11), (12) и (8). Найдем сначала дискриминант ( small D ) из формулы (11). Для этого подставим 

 |
Подставляя значения 

 |
Найдем другую сторону ( small b ) из формулы (8). Подставляя значения 

 |
Ответ: 
Видео:ЕГЭ 2017 | Задание 3 | Найдите радиус окружности ... ✘ Школа ПифагораСкачать

Признаки прямоугольника
Признак 1. Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.
Признак 2. Если квадрат диагонали параллелограмма равен сумме квадратов его смежных сторон, то этот параллелограмм является прямоугольником.
Признак 3. Если углы параллелограмма равны, то этот параллелограмм является прямоугольником.
Видео:Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать

«решение заданий В-3» егэ
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Видео:Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
Сертификат и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Подготовка к ЕГЭ В 3
Уметь выполнять действия с геометрическими фигурами, координатами и векторами Решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей) Решать простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов); использовать при решении стереометрических задач планиметрические факты и методы Определять координаты точки; проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами
Повторение: а b а
Площадь треугольника a ha a b c a b g
Площадь трапеции h a b Площадь параллелограмма h a
Площадь круга r Площадь кругового сектора r α
Длина окружности r Длина дуги окружности r α
Сложение векторов Правило треугольника: А В С Для любых трех точек A,B,C имеет место равенство
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см x 1 см. Ответ дайте в квадратных сантиметрах.
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
2. Найдите (в см2) площадь фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.).
4. Найдите площадь треугольника, вершины которого имеют координаты (0;0), (10;8), (8;10).
5. Найдите площадь параллелограмма, вершины которого имеют координаты (1;7), (4;1), (4;4), (1;10).
6. Найдите (в см2) площадь фигуры, изображенной на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). В ответе запишите S/π.
7. Найдите площадь сектора круга радиуса , центральный угол которого равен 90˚ .
8. Периметр треугольника равен 88, а радиус вписанной окружности равен 10. Найдите площадь этого треугольника.
9. Площадь сектора круга радиуса 15 равна 105. Найдите длину его дуги.
10. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150. Боковая сторона треугольника равна 19. Найдите площадь этого треугольника. 150 19
11. Найдите угловой коэффициент прямой, проходящей через точки с координатами (-2;0)и (0;11). Общее уравнение прямой: y = kx + b 12. Найдите площадь прямоугольника, если его периметр равен 116, а отношение соседних сторон равно 4:25. a b a=4k b= 25k P=2(4k+25k)=58k 58k=116 k=2 a=8 b= 50 S=8·50= 400
13. Площадь параллелограмма равна 36, две его стороны равны 12 и 24. Найдите большую высоту этого параллелограмма. 12 24 S=ha 36=h· 12 h=3
14. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30 градусов. Найдите боковую сторону треугольника, если его площадь равна 1521. 30˚ h a a
15. Найдите ординату точки пересечения прямой, заданной уравнением 21х-20у=60 , с осью Oy. 18. Две стороны прямоугольника ABCD равны 9 и 40. Найдите длину суммы векторов АВ и AD .
19. Найдите абсциссу центра окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (5; 10) , (5;2) , (-1;2) , (-1;10) .
Диагонали ромба ABCD равны 48 и 55. Найдите длину вектора . А В С D
Найдите площадь трапеции, вершины которой имеют координаты (2;1), (10;1), (9;9), (6;9). Реши самостоятельно:
Средняя линия и высота трапеции равны соответственно 36 и 4. Найдите площадь трапеции. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен . Найдите боковую сторону треугольника, если его площадь равна 289. Площадь сектора круга радиуса 41 равна 123. Найдите длину его дуги. 4. Найдите угловой коэффициент прямой, проходящей через точки с координатами и .
5. Точки O(0,0), , , являются вершинами четырехугольника. Найдите ординату точки P пересечения его диагоналей. 6. Найдите абсциссу центра окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно , , , . 7. Диагонали ромба ABCD равны 42 и 56. Найдите длину вектора . 8. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
9. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Курс повышения квалификации
Охрана труда
- Сейчас обучается 95 человек из 44 регионов
Курс профессиональной переподготовки
Библиотечно-библиографические и информационные знания в педагогическом процессе
- Сейчас обучается 348 человек из 64 регионов
Курс профессиональной переподготовки
Охрана труда
- Сейчас обучается 215 человек из 50 регионов
Ищем педагогов в команду «Инфоурок»
Видео:Задание 16 ОГЭ по математике. Две окружности одна описана около квадрата, другая вписана в него.Скачать

Дистанционные курсы для педагогов
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 523 175 материалов в базе
Другие материалы
- 08.01.2017
- 5238
- 5
- 08.01.2017
- 548
- 0
- 08.01.2017
- 564
- 1
- 08.01.2017
- 465
- 5
- 08.01.2017
- 1472
- 3
- 08.01.2017
- 744
- 0
- 08.01.2017
- 336
- 0
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 08.01.2017 1945
- PPTX 1.9 мбайт
- 2 скачивания
- Оцените материал:
Настоящий материал опубликован пользователем Гончарова Ирина Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 6 лет и 7 месяцев
- Подписчики: 1
- Всего просмотров: 37500
- Всего материалов: 27
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Задание 3 ЕГЭ по математике. Урок 73Скачать
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В России планируют создадут сеть центров для подростков «группы риска»
Время чтения: 1 минута
Петербургских школьников с 7 по 11 классы перевели на дистанционное обучение
Время чтения: 1 минута
Проверки показали невыполнение в ряде регионов санитарных правил в школах
Время чтения: 1 минута
В Петербурге открыли памятник работавшим во время блокады учителям
Время чтения: 1 минута
Ставропольских школьников с 1 по 8 класс перевели на дистанционное обучение
Время чтения: 2 минуты
Полный перевод школ на дистанционное обучение не планируется
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
🔥 Видео
Радиус описанной окружностиСкачать

Геометрия В прямоугольнике ABCD известно, что AB = 12 см, угол CAD = 30. Найдите радиус окружностиСкачать

Радиус окружности описанной около равностороннего треугольникаСкачать
ЕГЭ профиль #3 / Радиус описанной окружности / Равносторонний треугольник / решу егэСкачать

ЕГЭ 2017 | Задание 3 | Найдите радиус ... ✘ Школа ПифагораСкачать

Задание 3 ЕГЭ по математике. Урок 72Скачать

Задание 24 ОГЭ по математике #7Скачать

Задание 26 Нахождение радиуса окружности описанной около треугольникаСкачать










