В кубе abcda1b1c1d1 в плоскости abcd найдите прямые параллельные а1б1

Вопрос по геометрии:

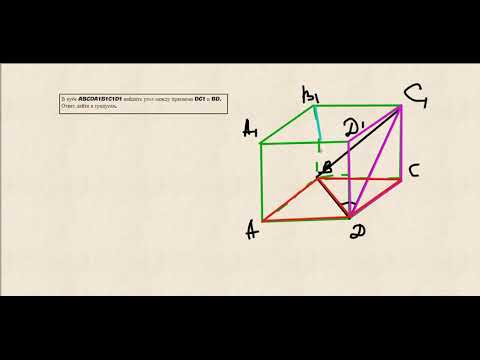
В кубе ABCDA1B1C1D1 в плоскости ABCD найдите прямые параллельные прямой B1C1

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

В кубе в плоскости ABCD B1C1||BC||AD

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:Геометрия Диагонали грани ABCD куба ABCDA1B1C1D1 пересекаются в точке O Найдите угол между прямымиСкачать

В кубе ABCDA1B1C1D1 укажите плоскость, параллельную плоскости A1BC1 и проходящую через три вершины куба.

Ответ:

Объяснение:

AA₁ = BB₁ и AA₁║BB₁, a BB₁ = CC₁ и BB₁║CC₁ как противоположные стороны квадратов, значит

AA₁║CC₁ и АА₁ = СС₁, значит

АС ║ А₁С₁

Аналогично, A₁D₁ = BC и A₁D₁║BC, значит

A₁B║D₁C

Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны.

Видео:№190. Дан куб ABCDA1B1C1D1. Найдите следующие двугранные углы: а) АВВ1ССкачать

Проверочная работа «13 задание ПРОФИЛЬ ЕГЭ математика»

Видео:В кубе ABCDA1B1C1D1 найдите угол между прямыми AD1 и В1D1. Ответ дайте в градусах.Скачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

ПРОФИЛЬ ЕГЭ математика

1. Дана правильная четырехугольная пирамида SABCD. Плоскость α параллельна прямой АС, проходит через точку В и середину высоты пирамиды.

а) Докажите, что плоскость α делит ребро SD в отношении 2 : 1, считая от точки D.

б) Найдите синус угла между плоскостью α и плоскостью ASC, если угол SAC равен 30°.

2. Боковое ребро правильной треугольной пирамиды SABC равно 6, а косинус угла ASB при вершине боковой грани равен Точка M — середина ребра SC, точка — середина ребра AC.

а) Докажите, что угол между прямыми BM и SA равен углу BMN.

б) Найдите косинус угла между прямыми BM и SA.

3. В основании правильной пирамиды PABCD лежит квадрат ABCD со стороной 9. Сечение пирамиды проходит через вершину В и середину ребра PD перпендикулярно этому ребру.

а) Докажите, что угол наклона бокового ребра пирамиды к её основанию равен 60°.

б) Найдите площадь сечения пирамиды.

4. В основании пирамиды SABCD лежит прямоугольник ABCD со стороной AB = 4 и диагональю BD = 7. Все боковые рёбра пирамиды равны 4. На диагонали BD основания ABCD отмечена точка E, а на ребре AS — точка F так, что SF = BE = 3.

а) Докажите, что плоскость CEF параллельна ребру SB .

б) Плоскость CEF пересекает ребро SD в точке Q. Найдите расстояние от точки Q до плоскости ABC.

5. В конус, радиус основания которого равен 6, вписан шар радиуса 3.

а) Изобразите осевое сечение комбинации этих тел.

б) Найдите отношение площади полной поверхности конуса к площади поверхности шара.

6. В пирамиде SABC в основании лежит правильный треугольник ABC со стороной Точка O — основание высоты пирамиды, проведённой из вершины S.

а) Докажите, что точка O лежит вне треугольника ABC.

б) Найдите объём четырёхугольной пирамиды SABCO.

7. Точка M середина ребра AB правильного тетраэдра DABC.

а) Докажите, что ортогональная проекция точки M на плоскость ACD лежит на медиане AP грани ACD.

б) Найдите угол между прямой DM и плоскостью ACD.

8. Основанием прямой треугольной призмы ABCA₁B₁C₁ является прямоугольный треугольник ABC с прямым углом C. Грань ACC₁A₁ является квадратом.

а) Докажите, что прямые CA₁ и AB₁ перпендикулярны.

б) Найдите расстояние между прямыми CA₁ и AB₁, если AC = 4, BC = 7.

9. Длины всех ребер правильной четырёхугольной пирамиды PABCD с вершиной P равны между собой. Точка M — середина бокового ребра пирамиды AP.

а) Докажите, что плоскость, проходящая через точки B и M и перпендикулярная плоскости BDP, делит высоту пирамиды пополам.

б) Найдите угол между прямой BM и плоскостью BDP.

а) Докажите, что B₁KLM — правильная пирамида.

ПРОФИЛЬ ЕГЭ математика

1. Точки A, B и C лежат на окружности основания конуса с вершиной S, причём A и C диаметрально противоположны. Точка M — середина BC.

а) Докажите, что прямая SM образует с плоскостью ABC такой же угол, как и прямая AB с плоскостью SBC.

б) Найдите угол между прямой SA и плоскостью SBC, если AB = 4, BC = 6 и

2. В кубе ABCDA₁B₁C₁D₁ все рёбра равны 4. На его ребре BB₁ отмечена точка K так, что KB = 3. Через точки K и C₁ построена плоскость α, параллельная прямой BD₁.

б) Найдите угол наклона плоскости α к плоскости грани BB₁C₁C.

3. В основании четырехугольной пирамиды SАВСD лежит параллелограмм АВСD c центром О. Точка N — середина ребра SC, точка L — середина ребра SA.

а) Докажите, что плоскость BNL делит ребро SD в отношении 1 : 2, считая от вершины S.

б) Найдите угол между плоскостями BNL и АВС, если пирамида правильная, SA = 8, а тангенс угла между боковым ребром и плоскостью основания пирамиды равен

4. Основание ABCD призмы — трапеция с основаниями AB = 2CD.

а) Докажите проходит через середину бокового ребра

б) Найдите угол между боковым ребром и этой плоскостью, если призма прямая, трапеция ABCD прямоугольная с прямым углом при вершине B, а BC = CD и

5. В правильной треугольной пирамиде SABC сторона основания AB равна 9, а боковое ребро SA = 6. На рёбрах AB и SC отмечены точки K и M соответственно, причём AK : KB = SM : MC = 2 : 7. Плоскость α содержит прямую KM и параллельна прямой SA.

а) Докажите, что плоскость α делит ребро SB в отношении 2 : 7, считая от вершины S.

б) Найдите расстояние между прямыми SA и KM.

6. Сторона правильной треугольной призмы ABCA₁B₁C₁ равна 8. Высота этой призмы равна 6.

а) Докажите, что плоскость, содержащая прямую и параллельная прямой делит пополам ребро

7. Дана треугольная пирамида DABC, точки M, N, P и Q лежат на рёбрах AB, BC, AD, CD, причём AM : MB = CN : NB = 3 : 1. Точки P и Q — середины рёбер DA и DC соответственно.

а) Докажите, что точки P, Q, M и N лежат в одной плоскости.

б) Найдите отношение многоугольников на которые делит плоскость PQM пирамиду.

8. ABCA ₁ B ₁ C ₁ — правильная призма, сторона AB равна 16. Через точки M и P, лежащие на рёбрах AC и BB1 соответственно, проведена плоскость α, параллельная прямой AB. Сечение призмы этой плоскостью — четырёхугольник, одна сторона которого равна 16, а три другие равны между собой.

а) Докажите что периметр сечения призмы плоскостью α больше 40.

б) Найдите расстояние от точки A до плоскости α, если упомянутый периметр равен 46.

9. В правильной треугольной призме ABCA₁B₁C₁ сторона основания а боковое ребро AA₁ = 5.

а) Найдите длину отрезка A₁K, где K — середина ребра BC.

10. В основании пирамиды SABCD лежит прямоугольник ABCD со стороной AB = 4 и диагональю BD = 7. Все боковые рёбра пирамиды равны 4. На диагонали BD основания ABCD отмечена точка E, а на ребре AS — точка F так, что SF = BE = 3.

а) Докажите, что плоскость CEF параллельна ребру SB .

б) Плоскость CEF пересекает ребро SD в точке Q. Найдите расстояние от точки Q до плоскости ABC.

ПРОФИЛЬ ЕГЭ математика

б) Найдите угол между плоскостью α и плоскостью ADD₁.

2. В правильном тетраэдре MNPQ через биссектрисы NA и QB граней MNP и QNP проведены параллельные плоскости.

а) Найдите отношение суммы объемов отсекаемых от MNPQ тетраэдров к объему MNPQ

б) Найдите расстояние между NA и QB, если ребро тетраэдра равно 1.

а) Докажите, что прямые B₁P и QB перпендикулярны.

б) Найдите площадь сечения куба плоскостью, проходящей через точку P и перпендикулярной прямой BQ, если ребро куба равно 10.

4. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки В₁ и С₁, причем ВВ₁ — образующая цилиндра, а отрезок АС₁ пересекает ось цилиндра.

а) Докажите, что угол АВС₁ прямой.

б) Найдите площадь боковой поверхности цилиндра, если AB = 20, BB₁ = 15, B₁C₁ = 21.

5. Дана треугольная пирамида DABC, точки M, N, P и Q лежат на рёбрах AB, BC, AD, CD, причём AM : MB = CN : NB = 3 : 1. Точки P и Q — середины рёбер DA и DC соответственно.

а) Докажите, что точки P, Q, M и N лежат в одной плоскости.

б) Найдите отношение многоугольников на которые делит плоскость PQM пирамиду.

6. В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB = 12 и Длины боковых рёбер пирамиды SA = 5, SB = 13, SD = 10.

а) Докажите, что SA — высота пирамиды.

б) Найдите расстояние от вершины A до плоскости SBC.

7. а) Дан прямоугольный параллелепипед Докажите, что все грани тетраэдра — равные треугольники (тетраэдр, обладающий таким свойством, называют равногранным).

8. В правильной треугольной призме ABCA₁B₁C₁ все рёбра равны 1.

а) Докажите, что прямая AB₁ параллельна прямой, проходящей через середины отрезков AC и BC₁.

б) Найдите косинус угла между прямыми AB₁ и BC₁.

9. Прямоугольник ABCD и цилиндр расположены таким образом, что AB — диаметр верхнего основания цилиндра, а CD лежит в плоскости нижнего основания и касается его окружности, при этом плоскость прямоугольника наклонена к плоскости основания цилиндра под углом 60°.

а) Докажите, что ABCD — квадрат.

б) Найдите длину той части отрезка BD, которая находится снаружи цилиндра, если радиус цилиндра равен

а) Докажите, что плоскость EFT проходит через вершину D₁.

б) Найдите угол между плоскостью EFT и плоскостью BB₁C₁.

ПРОФИЛЬ ЕГЭ математика

а) В каком отношении плоскость ETD₁ делит ребро BB₁?

б) Найдите угол между плоскостью ETD₁ и плоскостью AA₁B₁.

2. В основании прямой треугольной призмы ABCA₁B₁C₁ лежит равнобедренный треугольник ABC с основанием AC. Точка K — середина ребра A₁B₁, а точка M делит ребро AC в отношении AM : MC = 1 : 3.

а) Докажите, что KM перпендикулярно AC.

б) Найдите угол между прямой KM и плоскостью ABC, если AB = 12, AC = 16 и AA₁ = 6.

3. В треугольной пирамиде SABC известны боковые рёбра: Основанием высоты этой пирамиды является середина медианы CM треугольника ABC. Эта высота равна 4.

а) Докажите, что треугольник ABC равнобедренный.

б) Найдите объём пирамиды SABC.

4. В основании правильной треугольной призмы ABCA₁B₁C₁лежит треугольник со стороной 6. Высота призмы равна 4. Точка N — середина ребра A₁C₁.

а) Постройте сечение призмы плоскостью BAN.

б) Найдите периметр этого сечения.

5. В основании MABCD лежит прямоугольник ABCD со сторонами AB = 4 и BC = все боковые ребра пирамиды равны 4. На диагонали BD основания ABCD отмечена точка Е, а на ребрах AM и AB — точка F и G соответственно так, что MF = BE = BG = 3.

а) Докажите, что плоскость GEF проходит через точку C.

б) Найдите длину отрезка, по которому плоскость GEF пересекает грань CMD пирамиды.

6. Длина ребра правильного тетраэдра ABCD равна 1. M — середина ребра BC, L — середина ребра AB.

а) Докажите, что плоскость, параллельная прямой CL и содержащая прямую DM, делит ребро AB в отношении 3 : 1, считая от вершины A.

б) Найдите угол между прямыми DM и CL.

7. Дана пирамида SABC, в которой

а) Докажите, что ребро SA перпендикулярно ребру BC.

б) Найдите расстояние между ребрами BC и SA.

8. Радиус основания конуса равен 12, а высота конуса равна 5.

а) Постройте сечение конуса плоскостью, проходящей через вершину конуса и взаимно перпендикулярные образующие.

б) Найдите расстояние от плоскости сечения до центра основания конуса.

9. В правильной четырёхугольной призме ABCDA₁B₁C₁D₁ сторона основания AB = 6, а боковое ребро На рёбрах AB, A₁D₁ и C₁D₁ отмечены точки M, N и K соответственно, причём AM = A₁N = C₁K = 1.

а) Пусть L — точка пересечения плоскости MNK с ребром BC. Докажите, что MNKL — квадрат.

б) Найдите площадь сечения призмы плоскостью MNK.

10. В правильной треугольной пирамиде SABC с вершиной S, все рёбра которой равны 4, точка N — середина ребра AC, точка O центр основания пирамиды, точка P делит отрезок SO в отношении 3 : 1, считая от вершины пирамиды.

а) Докажите, что прямая NP перпендикулярна прямой BS.

б) Найдите расстояние от точки B до прямой NP.

💡 Видео

№110. Докажите, что в параллелепипеде ABCDA1B1C1D1 плоскость A1DB параллельна плоскости D1CB1.Скачать

Параллельность прямой и плоскости. 10 класс.Скачать

№344. Диагонали куба ABCDA1B1C1D1 пересекаются в точке О. Найдите число k такое,Скачать

№191. Дан куб ABCDA1B1C1D1. Докажите, что плоскостиСкачать

№81. Изобразите параллелепипед ABCDA1B1C1D1 и отметьте точки М и N соответственноСкачать

Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Угол между прямыми в пространстве. Практическая часть. 10 класс.Скачать

Решение задач (находим угол в кубе)Скачать

№194. Ребро куба равно а. Найдите расстояние между скрещивающимися прямыми, содержащимиСкачать

Готовимся к ЕГЭ. Стереометрия. Базовые задачи. Угол между прямыми. КубСкачать

№83. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей черезСкачать

№116. Дан параллелепипед ABCDA1B1C1D1. Докажите, что: а) DC⊥B1C1, и AB⊥A1DСкачать

Найти в кубе угол между двумя прямымиСкачать

Угол между прямыми в пространстве. 10 класс.Скачать

№19. Стороны АВ и ВС параллелограмма ABCD пересекают плоскость αСкачать