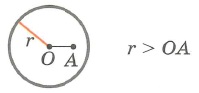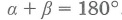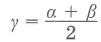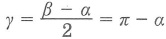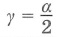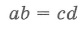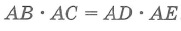Метрические отношения в окружности

Свойства окружностей. Прямые, отрезки и углы, связанные с окружностью.
Взаимное расположение окружности и прямой, окружности и точки, двух окружностей.
Свойства углов, связанных с окружностью. Метрические соотношения в окружности.

Прямые, отрезки и углы, связанные с окружностью:

Центральный угол измеряется дугой, на которую он опирается. Если отнести длину этой дуги к радиусу окружности то получится радианная мера угла.

Взаимное расположение окружности и прямой:

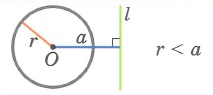
1. Окружность и прямая не имеют общих точек

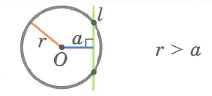
2. Окружность и прямая имеют 2 общие точки (l — секущая)

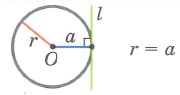
3. Окружность и прямая имеют 1 общую точку (l — касательная)

Взаимное расположение окружности и точки:

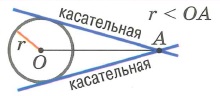
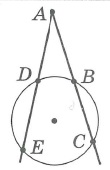
1. Точка лежит вне окружности (2 касательные через точку А)

2. Точка лежит внутри окружности (нет касательных через точку А)

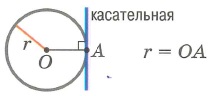
3. Точка лежит на окружности (1 касательная через точку А)

Взаимное расположение двух окружностей:

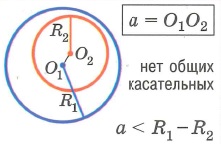
1. Одна окружность лежит внутри другой.

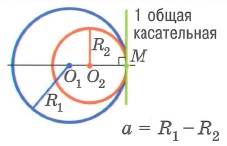
2. Одна окружность касается другой изнутри.

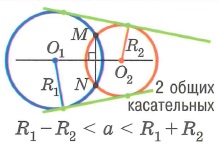
3. Окружности пересекаются.

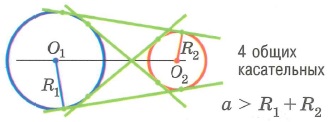
4. Одна окружность касается другой снаружи или одна окружность лежит вне другой.

Свойства углов, связанных с окружностью:

Вписанный угол равен половине центрального, опирающегося на ту же дугу:

Все вписанные углы, опирающиеся на одну и ту же дугу равны:Все вписанные углы, опирающиеся на одну и ту же хорду, вершины которых лежат по одну сторону от этой хорды, равны:

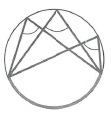
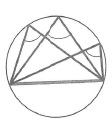
Любые два вписанных угла, опирающиеся на одну и ту же хорду, вершины которых лежат по разные стороны хорды, составляют в сумме 180°=π

Все вписанные углы, опирающиеся на диаметр, прямые:

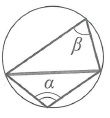
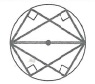
Угол между пересекающимися хордами:

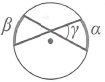
Угол между секущими, пересекающимися вне окружности:

Угол между касательной и секущей:

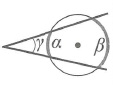
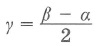
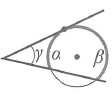
Угол между касательными:

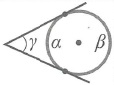
Угол между касательной и хордой:

Метрические соотношения в окружности (длины отрезков):

Отрезки пересекающихся хорд связаны соотношением:

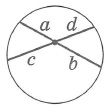
Отрезки касательных, проведенных из общей точки, равны:

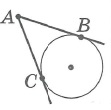
Квадрат длины отрезка касательной равен произведению длин отрезков секущей, проведенной из той же точки:

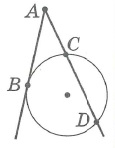
Произведения длин отрезков секущих, проведенных из общей точки, равны:

Консультации и техническая
поддержка сайта: Zavarka Team

Отрезки и прямые, связанные с окружностью. Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Свойства хорд и дуг окружности

Теоремы о длинах хорд, касательных и секущих

Доказательства теорем о длинах хорд, касательных и секущих

Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках

Фигура	Рисунок	Определение и свойства
Окружность
Круг
Радиус
Хорда
Диаметр
Касательная
Секущая

Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Радиус

Отрезок, соединяющий центр окружности с любой точкой окружности

Хорда

Отрезок, соединяющий две любые точки окружности

Диаметр

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Касательная

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Секущая

Прямая, пересекающая окружность в двух точках

Свойства хорд и дуг окружности

Фигура	Рисунок	Свойство
Диаметр, перпендикулярный к хорде		Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды		Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Равные хорды		Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
Хорды, равноудалённые от центра окружности		Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
Две хорды разной длины		Большая из двух хорд расположена ближе к центру окружности.
Равные дуги		У равных дуг равны и хорды.
Параллельные хорды		Дуги, заключённые между параллельными хордами, равны.

Диаметр, перпендикулярный к хорде

Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Равные хорды

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Хорды, равноудалённые от центра окружности

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Две хорды разной длины

Большая из двух хорд расположена ближе к центру окружности.

Равные дуги

У равных дуг равны и хорды.

Параллельные хорды

Дуги, заключённые между параллельными хордами, равны.

Теоремы о длинах хорд, касательных и секущих

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Фигура	Рисунок	Теорема
Пересекающиеся хорды
Касательные, проведённые к окружности из одной точки
Касательная и секущая, проведённые к окружности из одной точки
Секущие, проведённые из одной точки вне круга

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Пересекающиеся хорды

Касательные, проведённые к окружности из одной точки

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Пересекающиеся хорды

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Касательные, проведённые к окружности из одной точки

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Доказательства теорем о длинах хорд, касательных и секущих

Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).

Тогда справедливо равенство

Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).

Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство

Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).

Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство

Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).

Точка B – точка касания. В силу теоремы 2 справедливы равенства

откуда и вытекает требуемое утверждение.

Теорема о бабочке

Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.

Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:

Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим

Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим

Воспользовавшись теоремой 1, получим

Воспользовавшись равенствами (1) и (2), получим

Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство

откуда вытекает равенство

что и завершает доказательство теоремы о бабочке.

Методическая система работы по теме «Метрические отношения в окружности»

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Методическая система по теме

«Метрические соотношения в круге»

Методическая система обучения — это упорядоченная совокупность взаимосвязанных и взаимообусловленных методов, форм и средств планирования и проведения, контроля, анализа, корректирования учебного процесса, направленных на повышение эффективности обучения учащихся.
Обучение только тогда эффективно, когда оно строится как методическая система.
Характерными чертами современной методической системы обучения являются:
• научно обоснованное планирование процесса обучения;
• единство и взаимопроникновение теоретической и практической подготовки школьников;
• высокий уровень трудностей и быстрый темп изучения учебного материала;
• максимальная активность и достаточная самостоятельность обучения;
• сочетание индивидуальной и коллективной работы школьников;
• насыщенность учебного процесса техническими средствами обучения;
• комплексирование различных предметов обучения.
Методическая система только тогда функционирует, если она определяется целями, задачами и содержанием обучения, если она включает планирование, контроль, анализ и корректировку учебного процесса.

Целью моей работы по данной теме является развитие УУД на уроках геометрии при подготовке к успешной сдаче экзаменов.

Проблема: Задания «Модуль Геометрия 2 часть» из ОГЭ по математике предназначены для желающих расширить и углубить свои знания по геометрии. Решению таких геометрических задач в школе уделяется мало времени, более того, задачи такого типа вообще не рассматриваются в учебниках. По статистике наименьшее число верных ответов приходится именно на геометрические задачи из 1 части, а ко второй части большинство выпускников даже не приступает.

Изменения, прошедшие в обществе за последнее время, наложили отпечаток на отечественную систему образования. Каждый учитель сегодня хотел бы видеть своего ученика-выпускника личностью самостоятельной, самоопределяющейся, самокритичной. Поэтому каждому учителю необходимо создать такую систему обучения, которая обеспечивала бы образовательные потребности каждого ученика в соответствии с его склонностями, интересами и возможностями. Технологии развивающего обучения отвечают запросам сегодняшнего дня, они и сегодня востребованы, а потому и современны. В отечественной педагогике обучение определяется как развивающее, если оно обеспечивает общее развитие личности — общие умственные способности, которые проявляются не только в успешном усвоении знаний, но и в оперировании ими; волю, проявляющуюся в умении поставить цели и мобилизовать себя на их реализацию; эстетические, нравственные и интеллектуальные чувства; познавательные и духовные потребности. Доминирующее значение в этом подходе придается развитию познавательных способностей учащихся. Развивающее обучение сегодня — обучение которое обеспечивает развитие целостной личности как индивидуальности, умеющей принимать собственные решения и брать ответственность на себя, испытывающей потребность самореализации своих способностей, склонностей, в творческой деятельности, включив их в содержание обучения (Занков Л.В., Кабанова — Меллер Е.Я., Якиманская И.С.) Из учения Выготского Л.С. о «зоне ближайшего развития» следует, что развитие умственных способностей возможно при предъявлении ученику специальных заданий, которые вызывают у ученика затруднение, при этом задания должны быть оптимальной трудности. Но это только предпосылка развития.

Основное условие и механизм развития учащихся – включение их в активную деятельность. Но чтобы активная деятельность действительно стимулировала развитие ученика, она должна направлять учащегося на решение поисковых, проблемных, творческих задач; быть хорошо описана и осознана учениками; быть мотивационной и разнообразной.

В рамках концепции развивающего обучения разработан ряд технологий, отличающихся целевыми ориентирами, особенностями содержания и методиками:

— Проблемно-поисковые технологии обучения

— Технологии исследовательской направленности

— Технологии моделирующего обучения

Основные черты обобщенной модели развивающего обучения:

— Процесс обучения представляется как творческий поиск решения познавательных задач

— Познавательная рефлексия над результатом и процессом познания

— Активная позиция учащегося в учебном процессе

— Позиция педагога – «партнер по учебному исследованию»

— Процессуальная целевая ориентация.

В практике преподавания ту или иную технологию в «чистом виде» увидишь редко. Потому что, как сказал Д. Пойа: «Хороших методов существует ровно столько, сколько существует хороших учителей».

Обоснование выбора темы: Научиться решать геометрические задачи из второй части можно и даже нужно. Для этого необходимо ознакомиться с различными методами решения, приемами и подходами. Решение таких задач позволит понять и расширить знания, углубить навык решения геометрических задач повышенного и высокого уровня сложности.

🎬 Видео