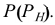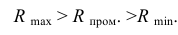Метод вспомогательных окружностей начертательная геометрия (5 видео)

Способ вспомогательных сфер в начертательной геометрии с примером

Способ вспомогательных сфер:

Этот способ широко используется при решении задач на построение линий пересечения поверхностей вращения с пересекающимися осями.

Прежде чем перейти к рассмотрению этого способа, рассмотрим частный случай пересечения поверхностей вращения, у которых оси совпадают. Такие поверхности называются соосными поверхностями вращения.

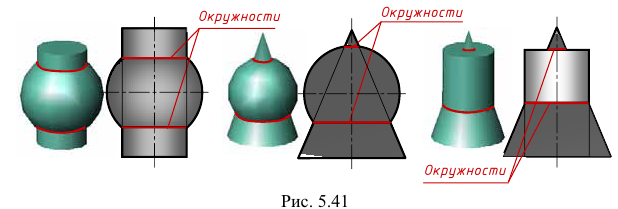
Линия пересечения соосных поверхностей — окружность, плоскость которой перпендикулярна оси поверхностей вращения. При этом, если ось поверхностей вращения параллельна плоскости проекций, то линия пересечения на эту плоскость проецируется в отрезок прямой линии (рис. 5.41).

Это свойство используют для построения линии взаимного пересечения двух поверхностей вращения с помощью вспомогательных сфер. При этом могут быть использованы концентрические (построенные из одного центра) и эксцентрические (проведенные из разных центров) сферы. Рассмотрим применение вспомогательных концентрических сфер — сфер с постоянным центром.

Следует отметить, что если плоскость осей поверхностей вращения не параллельна плоскости проекций, то окружности, по которым пересекаются поверхности, будут проецироваться в эллипсы, а это усложняет решение задачи. Поэтому способ вспомогательных сфер следует применять при следующих условиях:

а) пересекающиеся поверхности должны быть поверхностями вращения;
б) оси этих поверхностей должны пересекаться, точку пересечения принимают за центр вспомогательных сфер;
в) плоскость, образованная осями поверхностей (плоскость симметрии), должна быть параллельна одной из плоскостей проекций.

Используя этот способ, можно построить линию пересечения поверхностей на одной проекции.

Рассмотрим пример построения линии пересечения цилиндра и конуса вращения (рис. 5.42).

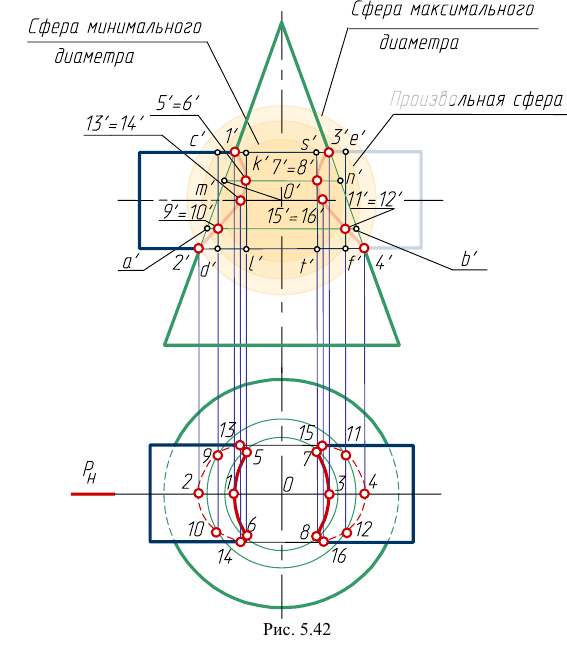
Точки 1, 2, 3, 4 определяются как точки пересечения контурных образующих поверхностей, принадлежащие плоскости пересечения осей (плоскости симметрии

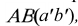
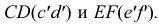
Из точки пересечения осей данных поверхностей (точки О’) построим вспомогательную сферу произвольного радиуса. Эта сфера будет одновременно соосна конусу и цилиндру и пересечет их по окружностям. Плоскости этих окружностей перпендикулярны соответствующим осям вращения. Фронтальные проекции этих окружностей — отрезки прямых. Проведенная сфера пересекает конус по окружности диаметра а цилиндр — по окружностям В пересечении окружности АВ с окружностями CD и EF получаем соответственно точки 9-10 и 1 1-12, принадлежащие линии пересечения.

Таким образом, можно построить достаточное количество точек искомой линии пересечения. При этом нужно иметь ввиду, что не все сферы могут быть использованы для решения задачи. Рассмотрим предельные границы вспомогательных сфер.

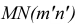
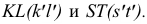
Радиус максимальной секущей сферы будет равен расстоянию от центра о’ до самой удаленной точки пересечения контурных образующих (от точки о’ до точек 2′ и 4′)- Минимальной секущей сферой должна быть такая сфера, которая касалась бы одной поверхности (большей) и пересекала вторую (меньшую). В данном примере минимальная сфера касается поверхности конуса по окружности и пересекает цилиндр по окружностям Пересекаясь между собой, окружности MN и KL дают точки линии пересечения 5 (5′) и 6 (6′), а окружности MN и ST — точки Это самые глубокие точки линии пересечения.

Для точности решения между максимальной и минимальной сферами необходимо построить дополнительные (промежуточные) сферы:

Если дополнительная сфера пересекает только одну данную поверхность, то такая сфера для решения задачи непригодна.

Для построения второй проекции линии пересечения можно использовать окружности, полученные от сечения конуса вспомогательными сферами.

Можно также построить дополнительные сечения поверхности, Точки 13-14 и 15-16, лежащие на контурных образующих цилиндра, являются точками границы видимости линии пересечения на горизонтальной проекции.

Рекомендую подробно изучить предметы:

Инженерная графика
Начертательная геометрия
Компас
Автокад
Черчение
Проекционное черчение
Аксонометрическое черчение
Строительное черчение
Техническое черчение
Геометрическое черчение

Ещё лекции с примерами решения и объяснением:

Выполнение и оформление чертежей по ГОСТ и ЕСКД
Виды в инженерной графике
Разрезы в инженерной графике
Сечения в инженерной графике
Развертка поверхности конуса
Шаровая поверхность
Винтовые поверхности
Способ вспомогательных секущих плоскостей

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Содержание

Построение линии пересечения конусов методом концентрических сфер
Алгоритм построения линии пересечения
Определение характерных точек
Определение промежуточных точек
Метод вспомогательных сфер
Способ концентрических сфер
💡 Видео

Видео:Метод эксцентрических сферСкачать

Построение линии пересечения конусов методом концентрических сфер

На рисунке ниже изображены два конуса вращения. Их оси i₁ и i₂, пересекаясь в точке O, образуют плоскость α(i₁∩i₂), которая параллельна фронтальной плоскости проекций π₂.

Для построения линии пересечения конусов, показанных на рисунке, целесообразно использовать метод концентрических сфер. Применение данного метода возможно в результате выполнения следующих условий:

пересекаются поверхности вращения (в частности, конус с конусом, конус с тором или цилиндром и т.д.);
оси поверхностей, пересекаясь между собой, образуют плоскость, которая параллельна одной из плоскостей проекций (в рассматриваемом примере пл. α(i₁∩i₂)∥π₂).

Видео:Метод концентрических сферСкачать

Алгоритм построения линии пересечения

Построение линии пересечения начинают с нахождения характерных точек, которые определяют ее границы и видимость относительно плоскостей проекций.

Определение характерных точек

Плоскость α, образованная пересекающимися осями i₁ и i₂, является общей плоскостью симметрии двух конусов. На рисунке показан ее горизонтальный след h_0α. Пересечение пл. α с конусами происходит по образующим S₂A, S₂B и S₁C, S₁D. Данные образующие ещё называют очерковыми, так как они очерчивают границы поверхностей (на фронтальной проекции).

Точки F’’, E’’, G’’, K’’, в которых пресекаются прямые S’’₂A’’, S’’₂B’’ с прямыми S’’₁C’’ и S’’₁D’’, определяют границы линии пересечения конусов в её проекции на плоскость π₂. Для нахождения F’, E’, G’ и K’ проводят линии связи из F’’, E’’, G’’, K’’ до горизонтального следа h₀_α.

Определение промежуточных точек

Воспользуемся методом концентрических сфер для нахождения множества промежуточных точек линии пересечения. Центром, из которого проводятся вспомогательные сферы, является точка O пересечения осей i₁ и i₂ рассматриваемых конусов.

Радиус R_max наибольшей сферы, применяемой в построениях, равен длине отрезка O’’G’’ – расстоянию от точки O до наиболее удаленной от нее точки G пересечения очерковых образующих.

Сфера минимального радиуса R_min – это сфера, вписанная в один из конусов и пересекающая другой. На рисунке ниже R_min= O’’H’’, где O’’H’’⊥ S’’₂B’’.

Рассмотрим построение точек 1, 2, 3 и 4. Сфера радиусом R_min пересекается с конусом, в которой она вписана, по окружности. Данная окружность проецируется на фронтальную плоскость проекций в виде отрезка P’’H’’. Кроме того, сфера радиусом R_min пересекается со вторым конусом по двум окружностям, диаметры которых соответственно равны длинам отрезков M’’N’’ и T’’L’’. Таким образом, на поверхности сферы лежат три окружности, которые пересекаются в общих для двух конусов точках 1, 2, 3 и 4.

Фронтальные проекции 1’’, 2’’, 3’’, 4’’ находятся на пересечении отрезков M’’N’’, T’’L’’ с P’’H’’. Для нахождения горизонтальных проекций 1’, 2’, 3’, 4’ точек 1, 2, 3, 4 на плоскости проекций π₁ из центра O’ проводим две окружности с диаметрами M’’N’’ и T’’L’’. Учитывая принадлежность точек соответствующим окружностям, по линиям связи определяем их горизонтальные проекции, как это показано на рисунке выше.

С помощью вспомогательной сферы радиусом R_var, где R_min ≤ R_var ≤ R_max, найдены точки 5 и 6. Как видно из построений, они находятся на пересечении двух окружностей, которые проецируются на фронтальную плоскость в виде отрезков W’’U’’ и Q’’V’’.

В описываемом способе решения каждая сфера играет роль посредника, содержащего на своей поверхности кривые (окружности), принадлежащие пересекающимся конусам. Действуя в соответствии с приведенным выше алгоритмом, необходимо найти такое количество точек, которое позволит определить геометрическую форму линии пересечения на каждой из проекций.

Найденные точки соединяем плавными кривыми с учетом их видимости. Как видно на рисунке, в результате пересечения конусов образовались две замкнутые линии. Они показаны красным цветом.

Видео:Линия пересечения двух поверхностей вращения (Метод вспомогательных сфер)Скачать

Метод вспомогательных сфер

Применение вспомогательных секущих сфер основано на свойстве соосных поверхностей вращения. Поверхности, оси которых совпадают, называются соосными (рис. 121).

Соосные поверхности вращения пересекаются по окружностям, лежащим в плоскостях, перпендикулярных их общей оси. Если общая ось поверхностей вращения параллельна одной из плоскостей проекций, то окружности на эту плоскость проецируются в виде отрезков прямых, соединяющих точки пересечения очерковых линий поверхностей (рис. 121).

Построить линию пересечения поверхностей с помощью вспомогательных секущих сфер можно двумя способами. В одном из них используются сферы, проведённые из одного общего центра, а в другом — сферы, проведённые из разных центров. В первом случае имеем способ концентрических сфер, во втором — способ эксцентрических сфер.

Видео:Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

Способ концентрических сфер

Применяется в том случае, когда:

• заданы две поверхности вращения;
• оси поверхностей пересекаются;
• плоскость осей параллельна одной из плоскостей проекций.

Пример 1. Построить линию пересечения конуса с цилиндром

Имеем две поверхности вращения с пересекающимися осями i и у, лежащими в плоскости 2 || щ. Следовательно, можно использовать вспомогательные концентрические сферы. Они проводятся в том поле, которому параллельна плоскость осей, т. е. в Каждая сфера пересечёт поверхности по окружностям, проецирующимся на Л1 в виде хорд, перпендикулярных осям конуса и цилиндра. При этом проводятся те из проекций окружностей, которые расположены в пределах изображения другой поверхности.

Определим центр сфер. Поскольку они должны быть соосны с каждой из заданных поверхностей, то центр 0 сфер находится в точке пересечения осей конуса и цилиндра. Очерковые образующие первых проекций конуса и цилиндра лежат в одной плоскости ?. Следовательно, точки A_h Bj, С], Dj их пересечения принадлежат искомой линии. А₂, В₂, С₂, D₂ е Ъ₂.

Определим максимальный и минимальный радиусы сфер. Очевидно, очерк сферы радиусом R_max пройдет через самую удаленную от 0 характерную точку А. Очерк сферы радиусом r_min должен касаться очерковых образующих одной поверхности, пересекая одновременно очерковые другой поверхности. Опустим из центра 0 перпендикуляры на очерковые образующие обеих поверхностей. Больший из этих перпендикуляров и будет Гщщ. Так как сфера коснулась конуса, то конус шире цилиндра. Тогда цилиндр пройдет сквозь конус, и в пересечении получатся две линии — линия входа цилиндра в конус и линия выхода его из конуса. А характерные точки Е и F_b найденные при помощи сферы радиусом r_min, являются крайними правой и левой этих линий. Проводя сферы радиусами r_mj_n и F₂, F₂ лежащие на очерках а₂ и Ь₂ тора, определены при помощи сферы 3. Её радиус равен расстоянию от центра 0₂ до крайних точек вертикального диаметра окружности основания тора. Очерки а₂ и Ь₂ будут проекциями линии пересечения сферы 3 с тором. Проекции а и Ь совпадут с осевой окружностью тора. Сфера 3 пересечёт конус по окружности п, проецирующейся на щ отрезком п. При пересечении п с осевой окружностью тора получаем Е и F. По линии связи переносим их на а₂ и Ь₂. Для уточнения формы искомой линии найдено ещё несколько промежуточных точек.