Доброго времени суток! Сегодня я хочу вам показать, как вычислять интегралы различными методами.
Сразу скажу, что пакет Matlab уже имеет набор стандартных решений интегралов, их количество достаточно для реализации разных задач, но иногда (актуально для учебных заведений) требуется реализовать метод, написав программу.
На самом деле такая реализация методов нерациональна, так как теряется смысл использования Matlab. Но не мне осуждать, мне — решать. Алгоритм реализации того или иного метода есть в интернете в свободном доступе, и сложности могут возникнуть только с синтаксисом языка в Matlab. Разберём типовую задачу решения интеграла:
Вычислить, разбив на количество отрезков n=100 
Следующими методами:
• прямоугольники вперёд (правыми прямоугольниками);
• прямоугольники назад (левыми прямоугольниками);
• трапеций;
• трапеций MATLAB;
• Симпсона MATLAB;
Как вы наверняка догадались, MATLAB — означает, что будем реализовывать через стандартную функцию.
Для начала объявим необходимые переменные:
- • Метод правых прямоугольников:
- • Метод левых прямоугольников:
- • Метод трапеций:
- • Метод трапеций MATLAB:
- • Метод Симпсона MATLAB:
- • Метод правых прямоугольников:
- • Метод левых прямоугольников:
- • Метод трапеций:
- • Метод трапеций MATLAB:
- • Метод Симпсона MATLAB:
- Интегрирование в Matlab
- Численное интегрирование в Matlab
- Методы прямоугольников
- Метод трапеций
- Метод Симпсона
- Символьное интегрирование в Matlab
- Заключение
- Интегрирование функций, заданных аналитически (формула прямоугольников, формула трапеций, формула Симпсона)
- 📸 Видео
• Метод правых прямоугольников:
Вывод:
s =
0.0526
• Метод левых прямоугольников:
Вывод:
s =
0.0526
• Метод трапеций:
Тут легче уже объявить функцию у.
Вывод:
F =
0.0526
• Метод трапеций MATLAB:
Просто, не так ли?
Вывод:
ans =
0.0531
Как видите, уже заметно, что у всех методов свои погрешности.
• Метод Симпсона MATLAB:
Совсем просто, не так ли? =)
Вывод:
ans =
0.0531
Как видите, ничего страшного.
Давайте для закрепления материала, разберём ещё одну задачку:
Интегрировать с шагом 0.001 
Следующими методами:
• прямоугольники вперёд (правыми прямоугольниками);
• прямоугольники назад (левыми прямоугольниками);
• трапеций;
• трапеций MATLAB;
• Симпсона MATLAB;
• Метод правых прямоугольников:
Вывод:
s =
0.1349
• Метод левых прямоугольников:
Вывод:
s =
0.1348
• Метод трапеций:
Вывод:
F =
0.1349
• Метод трапеций MATLAB:
Вывод:
ans =
0.1363
• Метод Симпсона MATLAB:
Вывод:
ans =
0.1363
Надеюсь, теперь у вас не возникнет проблем с вычислением интегралов в Matlab.
Если у вас остались вопросы, то задавайте их в комментариях.
Видео:Метод левых, правых и средних прямоугольниковСкачать
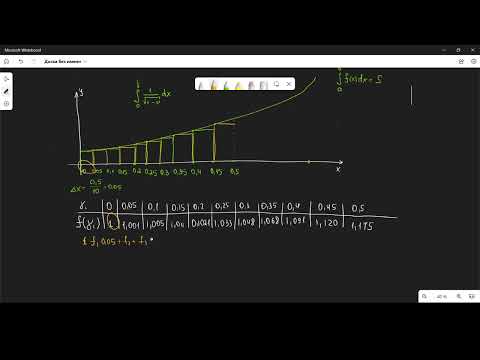
Интегрирование в Matlab
Доброго времени суток! Мы продолжаем говорить о численных методах. И сегодня мы поговорим о реализации численных методов интегрирования в среде Matlab.
Видео:Численное интегрирование: Методы Левых Правых прямоугольников, Трапеций, Симпсона c++Скачать

Численное интегрирование в Matlab
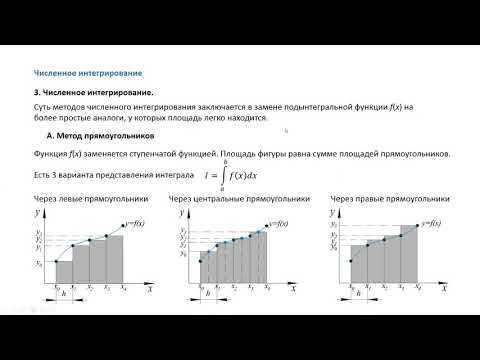
Геометрический смысл интегрирования — это нахождение площади, которая находится под интегрируемой функцией. 
Численное интегрирование не только в Matlab, но и в других средах, строится именно на нахождении площади. Для начала мы разберем простые методы:
Методы прямоугольников
- метод правых прямоугольников
- метод левых прямоугольников
- метод средних прямоугольников
Суть их в построение под кривой прямоугольников одинаковый ширины и нахождение их суммарной площади.
Также, следует отметить, что метод средних прямоугольников является более точным и предпочтительно использовать именно этот метод численного интегрирования, если у вас стоит выбор из этих трех методов. Эту точность можно доказать с помощью разложения в ряд Тейлора.
Необходимо посчитать интеграл функции f(x) = xe sin(x) x с шагом разбиения h = 0.02 на интервале от 0 до 1.
Функция feval (родственник функции eval) — интерпретирует и вычисляет текстовую строку, которая может содержать либо арифметическое выражение, либо инструкцию, либо обращение к функции, однако, в отличии от eval, интерпретирует и вычисляет текстовую строку, которая может содержать либо арифметическое выражение, либо инструкцию, либо обращение к функции.
Метод трапеций

В Matlab метод трапеций реализован двумя функциями:
- cumtrapz()
- trapz()
Первую функцию обычно используют при работе с табличными данными или векторами. Откликом функции является n-интегралов, где n — число элементов вектора или элементов в каждом столбце матрицы. Следующие примеры отображают работу этой функции.
Пусть функция y(x) имеет значения, представленные в виде следующего вектора: y = [1,2,3,4,5,6,7,8,9,10] . Необходимо вычислить:
При этом a = 1; b = 1, 2, 3, 4 …,10.
Пишем в Matlab:
Теперь рассмотрим вариант работы с вектором и матрицей:
Функция y(x) задана в виде матрицы y(x) = [1 3 5; 3 5 7; 4 6 8; 4 7 9; 5 7 10] . При этом аргумент представляет собой вектор: x = [1,3,7,9,10].
Вторая функция для интегрирования, работающая по методу трапеций Matlab — trapz(). Наиболее используемая студентами, так как позволяет работать не только с векторами и матрицами, но и с аналитической формой подынтегральной функции. Выглядит это примерно так:
Необходимо вычислить определённый интеграл в диапазоне от 1 до 10 с шагом 0.5 для заданной функции:
Как видите, ничего сложного. А иногда даже удобнее некоторых онлайн сервисов для расчёта интегралов.
Метод Симпсона

В Matlab интегрирование с помощью метода Симпсона производит функция quad. Сразу разберем пример.
Вычислить определённый интеграл с точностью 10 -4 методом Симпсона.
Точность вычислений задается 4 параметром функции quad. Также, следует отметить, что в задании нижним пределом является 0, а мы использовали число 0.001. Это связано с тем, что при подстановке 0 функция не определена, а точнее, натуральный логарифм не существует.
Ну и реализация этого метода вручную приведена здесь для общего развития. Этим я хочу подчеркнуть, что практически любой метод или алгоритм возможно написать самому, а не пользоваться стандартными методами Matlab.
Видео:Метод прямоугольников для нахождения определенного интегралаСкачать

Символьное интегрирование в Matlab
Часто нам необходимо найти интеграл от какой либо функции, не зная пределов интегрирования. Тогда нам нужно взять интеграл в общем или символьном виде. В Matlab за символьное интегрирование отвечает функция int. Она принимает как минимум 2 параметра: 1 — функция, 2 — имя переменной по которой берется интеграл. int(fun, var). Рассмотрим короткий пример:
Вычислить неопределённый интеграл:
Следует отметить, что функция int также может считать и определенные интегралы, для этого нужно задать пределы интегрирования в 3 и 4 параметры функции соответственно.
Заключение
На этом я хочу закончить сегодняшнюю тему «Интегрирование в Matlab». Не забывайте, что Matlab позволяет программировать сложные алгоритмы, а не только использовать встроенный функционал. Любой численный метод можно реализовать и вызывать как функцию. Если у вас остались вопросы, то задавайте их в комментариях.
В этот раз без исходников, примеры небольшие.
Видео:Метод левых прямоугольников, разбор задачиСкачать
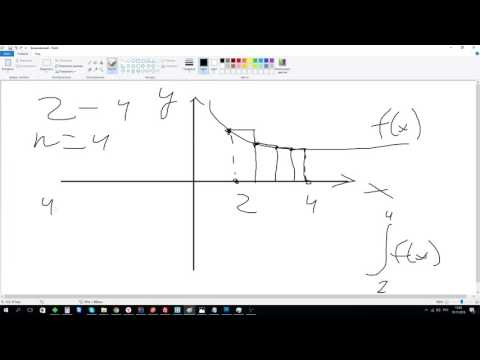
Интегрирование функций, заданных аналитически (формула прямоугольников, формула трапеций, формула Симпсона)
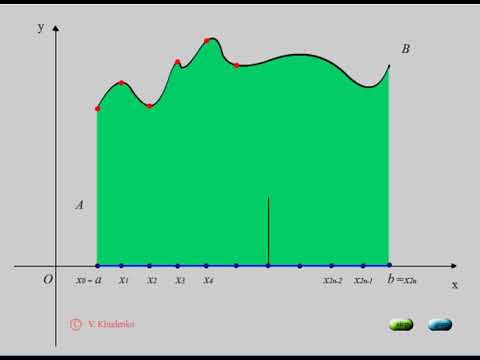
С геометрической точки зрения определенный интеграл
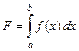
есть площадь фигуры, ограниченная графиком функции 
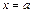
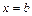
Разделим отрезок 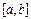

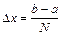
Тогда координата правого конца i-го отрезка определяется по формуле
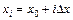
где 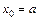
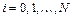
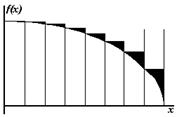 | 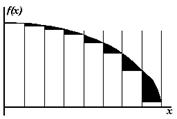 |
| Рис. 6.4. Метод левых прямоугольников | Рис. 6.5. Метод правых прямоугольников |
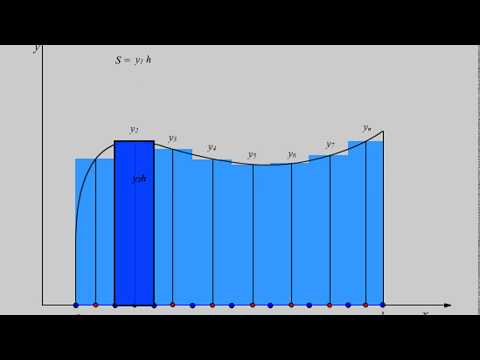
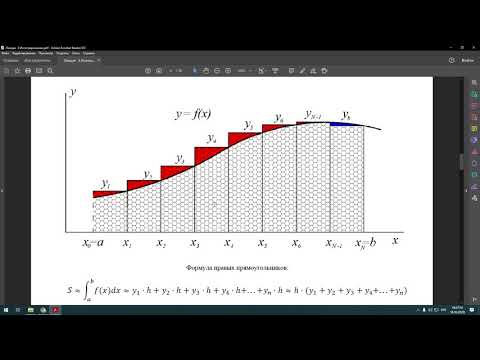
Простейшая оценка площади под кривой 
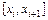
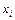
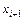
Значение определенного интеграла вычисляется по формулам
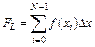
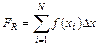
для методов левых и правых прямоугольников, соответственно.
Можно повысить точность вычисления определенного интеграла, если заменять реальную функцию на каждом интервале 
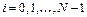
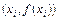
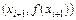
В этом случае фигура, ограниченная графиком функции и прямыми 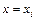
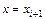
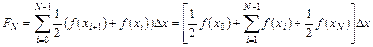
Более высокая точность вычисления интегралов обеспечивается при использовании параболической интерполяции (полиномом второй степени) по трем соседним точкам:
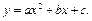
Более высокая точность вычисления интегралов обеспечивается при использовании параболической интерполяции (полиномом второй степени) по трем соседним точкам:
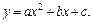
Для нахождения коэффициентов a, b, c полинома, проходящего через точки 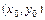
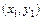

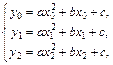
относительно неизвестных a, b, c.
Решив систему (6.18) относительно неизвестных a, b, c любым известным методом (например, Крамера), подставив найденные выражения в (6.17) и выполнив элементарные преобразования, получаем 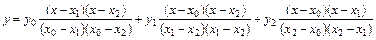
Площадь под параболой 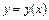
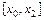
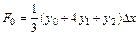
где 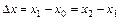
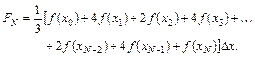
Обратите внимание на то обстоятельство, что в формуле Симпсона N должно быть четным числом.
Пример 6.2. Вычисление интеграла 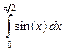
>> f=inline(‘sin(x)’);% задание подынтегральной функции
>> Xmin=0;
>> Xmax=pi/2;
>> N=2001;
>> i=1:N;
>> dx=(Xmax-Xmin)/(N-1);% шаг интегрирования
>> x=Xmin:dx:Xmax; % вычисление координат узлов сетки
>> y=feval(f,x);% вычисление значений функции в узлах сетки
% вычисление интеграла по формуле правых прямоугольников
>> m=2:N;
>> y1(m-1)=y(m);
>> Fr=sum(y1)*dx
Fr =
1.0004
>> Fr-1
ans =
E-004
% вычисление интеграла по формуле левых прямоугольников
>> m=1:N-1;
>> y1(m)=y(m);
>> Fl=sum(y1)*dx
Fl =
0.9996
>> Fl-1
ans =
-3.9295e-004
% вычисление интеграла методом трапеций
>> s=0;
for i=2:N-1
s=s+y(i);
End;
Ft=(0.5*y(1)+s+0.5*y(N))*dx
Ft =
1.0000
>> Ft-1
ans =
-5.1456e-008
% вычисление интеграла методом Симпсона
>> s=0;
for i=2:N-1
if i-2*ceil(i/2)==0
k=4;
Else
k=2;
End;
s=s+k*y(i);
End;
Fs=(y(1)+s+y(N))*dx/3
Fs =
1.0000
>> Fs-1
ans =
E-015
Для вычисления значений определенных интегралов в пакете MATLAB имеются следующие функции quad( ), quadl( ), trapz( ), cumtrapz( ), которые имеют следующий синтаксис.
>> q = quad(fun,a,b)% возвращает значение интеграла от функции
% fun на интервале [a,b], при вычислении
% используется адаптивный метод Симпсона.
>> q = quad(fun,a,b,tol)% возвращает значение интеграла от
% функции fun с заданной относительной
% погрешностью tol (по умолчанию tol=10 -3 )
>> q = quad(fun,a,b,tol,trace)% возвращает значение интеграла от
% функции fun на интервале [a,b] на
% каждом шаге итерационного
>> q = quad(fun,a,b,tol,trace,p1,p2. )% возвращает значение
% интеграла от функции fun
% на на интервале [a,b] на
% p1, p2, … — параметры,
% передаваемые в функцию
>> [q,fcnt] = quadl(fun,a,b. )% возвращает в переменную fcnt
% дополнительно к значению
% интеграла число выполненных
Функция quadl( )возвращает значения интеграла, используя для вычислений метод Лоббато (Lobbato). Синтаксис функции аналогичен синтаксису функции quad( ).
q = quadl(fun,a,b)
q = quadl(fun,a,b,tol)
q = quadl(fun,a,b,tol, ‘trace ‘)
q = quadl(fun,a,b,tol, ‘trace ‘,p1,p2. )
[q,fcnt] = quadl(fun,a,b. )
Пример 6.3. Вычисление интеграла 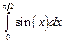
>> q=quad(‘sin’,0,pi/2,10^-4)
q =
1.0000
>> q-1
ans =
-3.7216e-008
>> q=quad(‘sin’,0,pi/2,10^-6,’trace’);
E-001 0.0896208493
E-001 0.4966040522
E-001 0.2032723690
E-001 0.2933317183
E-001 0.4137750613
>> q-1
ans =
-2.1269e-009
>> [q,fnct]=quad(‘sin’,0,pi/2,10^-6,’trace’);
E-001 0.0896208493
E-001 0.4966040522
E-001 0.2032723690
E-001 0.2933317183
E-001 0.4137750613
>> 17
Функция trapz( ) вычисляет интеграл, используя метод трапеций. Синтаксис функции trapz( ):
Z = trapz(Y)% возвращает значение определенного интеграла, в
% предположении, что X=1:length(Y)
Z = trapz(X,Y)% возвращает значение интеграла
% на интервале [X(1),X(N)]
Z = trapz(. dim)% интегрирует вектор Y, формируемый из чисел,
% расположенных в размерности dim
Функция cumtrapz( ) вычисляет интеграл, как функцию с переменным верхним пределом. Синтаксис функции cumtrapz( ) аналогичен синтаксису функции trapz( ).
Z = cumtrapz(Y)
Z = cumtrapz(X,Y)
Z = cumtrapz(. dim)
Пример 6.4. Вычисление определенного интеграла 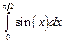
>> x=0:0.01:pi/2;% задание координат узловых точек
>> y=sin(x);% вычисление значений подынтегральной функции в
>> trapz(y)% вычисление значения интеграла, в предположении о
% том, что шаг интегрирования равен единице
ans =
99.9195
>> trapz(x,y)% вычисление значения интеграла на отрезке 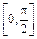
% шагом интегрирования 0.01
ans =
0.9992
Пример 6.5. Вычисление интеграла с переменным верхним пределом
>> x=0:0.01:3*pi/2;% задание координат узловых точек
>> y=sin(x);% вычисление значений подынтегральной функции в
>> z=cumtrapz(x,y);% вычисление значений интеграла с
% переменным верхним пределом в узловых
>> plot(x,y,x,z)% построение графиков подынтегральной функции и
📸 Видео
метод прямоугольниковСкачать
Вычисление определенных интегралов. Методы вычислений в MATLAB. Урок 68Скачать

Метод левых и метод правых прямоугольниковСкачать
3.2 Численное интегрирование (лекция)Скачать
3. Численные методы расчета определенного интеграла: прямоугольников, трапеции, парабол (Симпсона)Скачать
MATLAB 04 Массивы и матрицыСкачать

Метод средних прямоугольниковСкачать
Метод СимпсонаСкачать
Cимплексный метод решения задачи линейного программирования (ЗЛП)Скачать

Метод наименьших квадратов. Линейная аппроксимацияСкачать

3.1 Численное дифференцирование (лекция)Скачать

Символьные и численные расчеты в MATLABСкачать

6 Теория: Определенный интеграл Метод левых, правых, центральных прямоугольников, трапеций, СимпсонаСкачать

Метод Жордана-Гаусса (метод прямоугольников). ВидеоурокСкачать

MatLab. Берем производную и интеграл в буквенном выражении.Скачать

Решение систем Д/У: 1. Знакомство с функциями odeXYСкачать

