Мера близости двух векторов

Дата публикации Oct 3, 2019

Впредыдущая статья о системах рекомендациймы несколько раз упоминали концепцию «мер сходства». Зачем? Потому что в Рекомендационных системах как алгоритмы контентной фильтрации, так и алгоритмы совместной фильтрации используют определенную меру сходства, чтобы найти, насколько равны два вектора пользователей или элементов между ними. Таким образом, в конце, мера сходства не больше, чем расстояние между векторами.

Примечание: помните, что вся моя работа, включая специальный репозиторий с применением всего этого контента и больше о Системах Рекомендаций, доступна в моемПрофиль GitHub,

В любом типе алгоритма наиболее распространенной мерой подобия является нахождение косинуса угла между векторами, то есть сходства косинусов. Предположим, что A — это список фильмов с рейтингом пользователя, а B — список фильмов с рейтингом пользователя B, тогда сходство между ними можно рассчитать как:

Математически косинусное сходство измеряет косинус угла между двумя векторами, спроецированными в многомерном пространстве. При построении в многомерном пространстве косинусное сходство фиксирует ориентацию (угол) каждого вектора, а не величину. Если вы хотите получить величину, вместо этого вычислите евклидово расстояние.

Сходство по косинусу выгодно, потому что даже если два одинаковых документа находятся далеко друг от друга на евклидовом расстоянии из-за размера (например, одно слово, появляющееся много раз в документе, или пользователь, часто видящий один фильм), они все равно могут иметь меньший угол между ними. Чем меньше угол, тем выше сходство.

На изображении выше показано количество появлений слов «sachin», «dhoni» и «cricket» в трех показанных документах. В соответствии с этим мы могли бы построить эти три вектора, чтобы легко увидеть разницу между измерением косинуса и евклидова расстояния для этих документов:

Теперь, регулярное косинусное сходство по определению отражает различия в направлении, но не в местоположении. Следовательно, использование метрики косинусного сходства не учитывает, например, разницу в рейтингах пользователей. Скорректированное косинусное сходство компенсирует этот недостаток путем вычитания среднего рейтинга соответствующего пользователя из каждой пары с равным рейтингом и определяется следующим образом:

Давайте возьмем следующий пример из Stackoverflow, чтобы лучше объяснить разницу между косинусом и скорректированным сходством косинусов:

Предположим, пользователь дает оценки в 0

5 для двух фильмов.

Интуитивно мы бы сказали, что у пользователей b и c одинаковые вкусы, и a довольно сильно отличается от них. Но регулярное косинусное сходство говорит нам неверную историю. В подобных случаях вычисление скорректированного косинусного сходства даст нам лучшее понимание сходства между пользователями.

Кстати, в нашемпредыдущая статья о Системах Рекомендациймы представили следующую функцию, чтобы найти скорректированное косинусное сходство:

И вы можете использовать эту функцию очень просто, просто кормя:

1. «Матрица»: это просто исходная матрица рейтингов, просмотров или того, что вы измеряете между пользователями и элементами вашего бизнеса
2. «Row_columns»: указывает 1, если вы будете измерять расстояния между столбцами, и 0 для расстояний между рядами
3. «Размер»: для желаемого размера результирующей матрицы. То есть при поиске сходства пользователей или элементов это будет просто количество пользователей или элементов. Таким образом, если у вас есть 500 уникальных пользователей, вы получите матрицу расстояний 500×500

Возьмите следующий пример в качестве ссылки:

Наконец, давайте кратко рассмотрим некоторые другие методы, которые можно использовать для вычисления подобия для систем рекомендаций, но также и для любого другого алгоритма на основе расстояния в машинном обучении:

• Евклидово расстояние: похожие элементы будут лежать в непосредственной близости друг от друга, если они нанесены в n-мерном пространстве.

Видео:Коллинеарность векторовСкачать

Алгоритмы поиска схожих объектов в рекомендательных системах

«Досмотрю вот это видео на YouTube и пойду спать! Ой, в рекомендациях еще одно интересное. Сон, прости…». «Закажу в IKEA только стулья. Ах, сайт показал мне еще посуду, постельное белье и новую кухню в сборке. Когда там следующая зарплата?». «Бесконечный плейлист любимых музыкальных жанров в СберЗвуке заряжает меня позитивом! Как специалистам удается создавать выборку специально для меня?».

Согласитесь, вы сталкивались с подобными мыслями при использовании интернет сервисов. Магическим образом пользователю предлагают новые и новые объекты: видеоролики, музыку, товары. Никакого волшебства здесь нет — это рутинная работа рекомендательных систем. Алгоритмы поиска похожих объектов в больших массивах данных органично вплелись в нашу жизнь и помогают нам делать почти осознанный выбор в той или иной области повседневных дел.

Модели рекомендаций можно использовать для поиска похожих объектов вне контекста продаж. Например, выявлять однообразные ответы операторов в чатах, распознавать будущих злостных неплательщиков кредитных обязательств по косвенным признакам или находить различные группы сотрудников, которым требуется рекомендовать курсы повышения квалификации, в зависимости от текущих навыков. Не стоит забывать и о сайтах знакомств, где рекомендательные алгоритмы будут подбирать собеседника по указанным критериям.

Статья описывает основные подходы к поиску схожих объектов в наборе данных и содержит вводный курс в мир рекомендательных систем. Представлены варианты подготовки данных. Информация будет полезна аналитикам, которые изучают python, и начинающим data-scientist’ам. Мы не будем останавливаться на подробном описании каждого метода и разбирать отличия контентных и коллаборативных рекомендательных систем. Базовая теоретических часть находится здесь, здесь и здесь. Нас интересует применение алгоритмов матчинга (matching, англ. Поиск схожих объектов) в повседневных задачах. К статье прилагается ноутбук на платформе Kaggle с основным кодом, который рекомендуем запускать одновременно с изучением текста.

Коэффициенты корреляции

Самым простым способом вычисления схожести объектов по числовым характеристикам является расчет коэффициента корреляции. Этот метод работает в большинстве повседневных задач, когда у каждого объекта исследования присутствует одинаковый набор метрик. Такая последовательность числовых характеристик называется вектор. Например, мы ищем похожие квартиры в городе: можно банально сравнивать общую и жилые площади, высоту потолков и количество комнат. Для разбора кода возьмем датасет (dataset, англ. Набор данных), в котором содержится информация об объектах недвижимости Сиднея и Мельбурна. Каждая строка таблицы – это отдельный вектор с числовыми характеристиками.

Рис. 1 Датасет с объектами недвижимости

Схожесть характеристик можно рассчитать несколькими способами. Если вы работаете с табличными данными – pandas.corr() является самым удобным. Сравним три объекта, выставленных на продажу.

Мы рассчитали схожесть двух пар объектов: нулевого с девятым и нулевого с шестым. Посмотрите на рисунок выше. Действительно, дома в первой паре подобны по характеристикам. У второй пары объектов заметно различаются общая площадь, год постройки и ренновации, количество спален.

По умолчанию pandas.corr() рассчитывает коэффициент корреляции Пирсона. Его можно сменить на метод Спирмена или Кендала. Для этого нужно ввести аттрибут method.

Для обработки нескольких строк можно создать матрицу корреляции, в которой будут отражены сразу все объекты, находящиеся в датасете. По опыту работы замечу, что метод визуализации хорошо работает с выборками до 100 строк. Далее график становится слабо читаемым. Тепловую матрицу можно рисовать с помощью специализированных библиотек или применить метод style.background_gradient() к таблице. Создадим матрицу корреляции с 10 записями. Чем темнее цвет ячейки – тем выше корреляция.

Рис. 2 Матрица корреляции 10 объектов недвижимости

Метод pandas.corr() сравнивает таблицу по столбцам. Обратите внимание, что для правильного рассчета корреляций между объектами недвижимости, исходную таблицу необходимо транспонировать — повернуть на 90*. Для этого применяется метод dataframe.T.

Сравнивать объекты парами интересно, но непродуктивно. Попробуем написать небольшую рекомендательную систему, которая подберет 10 объектов недвижимости, которые максимально похожи на образцовый. За эталон примем случайный дом, например, с порядковым номером 574.

Рис. 3 Результат работы простейшей рекомендательной системы

Алгоритм отобрал 10 наиболее похожих на образец домов. Все представленные объекты недвижимости имеют одинакое количество спален и ванных комнат, примерно равные жилые и общие площади, и занимают только один этаж. В дополнении на Kaggleпредставлен второй вариант решения задачи, который последовательно перебирает все строки таблицы.

Метод pandas.corr() может сравнивать векторы (объекты), у которых отсутствуют некоторые значения. Это свойство удобно применять, когда нет времени или смысла искать варианты заполнения пропусков.

Косинусное расстояние

Эту метрику схожести объектов в математике обычно относят к методам расчета корреляции и рассматривают вместе с коэффициентами корреляции. Мы выделили ее в отдельный пункт, так как схожесть векторов по косинусу помогаем в решении задач обработки естественного языка. Например, с помощью данного алгоритма можно находить и предлагать пользователю похожие новости. Косинусное расстояние так же часто называют конисусной схожестью, диапазон значений метрики лежит в пределах от 0 до 1.

Разберем простейший алгоритм поиска похожих текстов и начнем с предобработки. В статье приведем некоторые моменты, полный код находится здесь. Для расчета косинусного расстояния необходимо перевести слова в числа. Применим алгоритм токенизации. Для понимания этого термина представьте себе словарь, в котором каждому слову приставлен порядковый номер. Например: азбука – 1348, арбуз – 1349. В процессе токенизации заменяем слова нужными числами. Есть более современный и более удачный метод превращения текста в числовой вектор — создание эмбеддингов с помощью моделей-трансформеров. Не углубляясь в тему трансформаций, отметим, что в этом случае каждое предложение предложение преврящается в числовой вектор длиной до 512 символов. При этом числа отражают взаимодействие слов друг с другом. Звучит, как черная магия, но здесь работает чистая алгебра. Советуем ознакомиться с базовой теорией о трансформерах, эмбеддингах и механизме «внимания» здесь и здесь.

В процессе преобразования новостных статей в токены и эмбеддинги получаем следующие результаты.

После векторизации текста можно сравнивать схожесть заголовков. Рассмотрим работу метода cosine_similarityиз библиотеки sklearn. Выведем два заголовка и узнаем, насколько они похожи.

Новости из мира техники и футбола далеки друг от друга. Косинусная схожесть равна 0.24%. Действительно, южнокорейский IT гигант и туринский футбольный клуб идейно практически не пересекаются.

Вернемся к первичной задаче раздела – поиску схожих статей для пользователя новостного сайта. Рассчитываем косинусное расстояние между векторизированными заголовками и показываем те, где коэффициент максимальный. В результате для новости под индексом 18 получаем следующие рекомендации.

Рис. 4 Результат работы рекомендательного алгоритма заголовков новостей

С высокой вероятностью пользователю, прочитавшему про восстанавливающийся рынок Европы будет интересно узнать про мировой кризис, рост цен и проблемы с валютой в азиатском регионе. Задача выполнена, переходим к заключительному алгоритму поиска схожих объектов.

Кластеризация

Третьим эффективным методом матчинга в большом объеме данных является кластеризация. Алгоритм разделяет записи по установленному количеству групп – кластеров. Задача кластеризации сводится к поиску идеального расположения центров групп — центроидов. Так, чтобы эти центры как бы группировали вокруг себя определенные объекты. Дистанция объекта от центра кластера рассчитывается целевой функцией. Подробнее о ней рекомендуем прочитать здесь. Алгоритм кластеризации представлен фукцией kMeans (англ, к-Средних) библиотеки sklearn.

Для примера алгоритма кластеризации возьмем 300 домов из первичного датасета с австралийской недвижимостью.

Первый шаг метода – поиск оптимального количества кластеров. Последовательно перебираем группы в диапазоне от 1 до 20 и рассчитываем значение целевой функции.

Отрисовываем значения целевой функции, получаем, так называемый, «локтевой график». Нас интересует точка, в которой происходит самый сильный изгиб. На рисунке 5 представлен искомый узел. При увеличении числа кластеров больше 4, значительного улучшения целевой функции не происходит.

Рис. 5 Поиск оптимального числа кластеров для группировки объектов недвижимости

Заново обучаем модель kMeans с необходимым числом кластеров. Для каждого объекта устанавливаем причастность к группе и сохраняем ее номер. Выбираем объекты одной группы.

Посмотрим на количество домов в группах.

«Нулевая» группа самая многочисленная и содержит типовые дома. В группы «один» и «два» попали объекты с громадной жилой площадью (столбец sqft_lot). Выборки представлены на рисунке 6.

Рис. 6 Объекты недвижимости с увеличенной площадью

Задача группировки объектов недвижимости с помощью алгоритма kMeans выполнена. Переходим к итогам.

Заключение

Мы рассмотрели три метода поиска схожих объектов в данных: коэффициенты корреляции, косинусное расстояние и метод k-средних. С помощью представленных инструментов можно решить большинство повседневных задач: найти схожие объекты с числовыми характеристиками, обработать текстовые записи или разбить массив данных на кластеры. Мы изучили основы матчинга и рекомендательных алгоритмов. В заключение отметим, что самые современные системы YouTube и TikTok в своей основе используют комбинации и улучшения указанных методов. Как видите, никакой магии в подборе любимых песен и роликов. Только чистая математика!

Видео:8 класс, 43 урок, Сумма двух векторовСкачать

ML: Embedding слов

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Введение

Перечислим в словаре $mathcal$ (vocabulary) размером V_DIM = V все значения некоторого качественного признака. Например, для 7 цветов в словаре будет V = 7 слов.
Чтобы нейронная сеть могла работать с таким признаком, его необходимо векторизовать. Это означает, что значениям признака ставятся в соответствие уникальные векторы с E_DIM = E компонентами. Тем самым качественный признак как-бы погружается (embedding) в вещественное векторное пространство. Каждое значение признака — это точка E-мерного пространства. Координаты точки-признака (как вещественные числа), можно отправлять на вход нейронной сети или любой другой модели машинного обучения.

При небольшом количестве значений признака подходит one-hot кодирование. В этом способе размерности векторов и число слов в словаре совпадают ( E = V), а вектор i-того слова состоит из нулей, кроме i-той позиции в которой стоит единица. One-hot кодировку можно интерпретировать как V-мерное пространство, каждая ось которого означает наличие ( 1) или отсутствие ( 0) данного значения. При этом векторы всех слов словаря попарно ортогональны:

One-hot кодировку иногда используют и для слов естественного языка, имеющего очень большой словарь.
Любой документ можно охарактеризовать суммой (или логическим OR) one-hot векторов его слов. Такой вектор документа называется мешком слов (bag of words, BoW), т.к. он отражает только количество или факт наличия (при OR) слов в документе, но не их порядок. Подобную простую векторизацию документов можно использовать, например, для их классификации или поиска.

У one-hot кодирования есть два недостатка: 1) при большом словаре векторное представление признаков становится очень громоздким, а число параметров модели увеличивается; 2) one-hot векторы не отражают близости различных слов словаря (если она существует).

Для устранения этих недостатков используют векторы относительно небольшой размерности с вещественными компонентами. Большинство их компонент отличны от нуля, поэтому это распределённое («размазанное») представление ( distributes representation). Такой подход называется Embedding или Word2Vec. Значения компонент векторов обычно определяют в процессе обучения. Предполагается, что векторы в E-мерном пространстве будут объединяться в кластеры по семантической (смысловой) близости слов, что упрощает обучение других слоёв модели. Впрочем, они могут быть и заданы (выше — это -компоненты цвета).

Для экспериментов с векторизацией слов естественного языка потребуется некоторый корпус текстов. Будем использовать короткие истории ROC Stories, подробное описание которых можно найти в документе NLP_ROCStories.html. Приведенные примеры на библиотеке PyTorch находятся в ноутбуке NN_Embedding_Learn.ipynb, для которого необходимы тексты из файла 100KStories.csv. Слегка почищенные истории можно скачать у нас на сайте

Видео:Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Векторы контекста

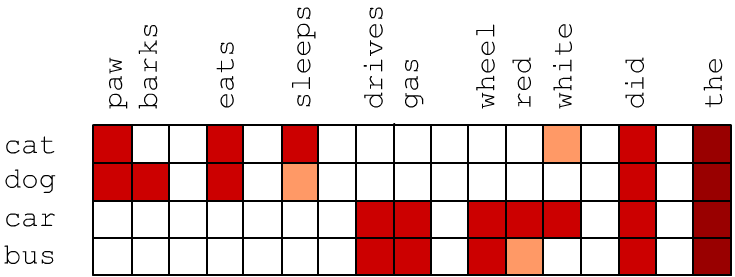
С каждым словом $w_i$ словаря $mathcal$ мы хотим связать вектор $mathbf_i=<u_. u_<i,text-1>>$ так, чтобы семантически близкие слова имели схожие векторы. В результате этого, например, слова dog, cat, rabbit в векторном пространстве должны оказаться рядом (образовать кластер) и при этом быть в отдалении от кластера слов car, bus, train.

Семантическая близость двух слов приводит к тому, что в текстах они встречаются в одинаковом контексте, т.е.в среднем их окружают одни и те-же слова. Возмём вначале векторы размерностью E_DIM, которая равна числу слов V_DIM в словаре ( E=V). Пусть у вектора i-го слова j-я компонента пропорциональна частоте $u_ = P(w_i,w_j)$ совместного появления слов $w_i$ и $w_j$ в одном предложении. Близкие по смыслу слова могут и не встречаться в одном предложении, но они имеют аналогичный контекст и схожие векторы. Ниже красным цветом условно отмечены высокие значения $P(w_i,w_j)$. Видно, что векторы cat и dog похожи и отличаются от векторов car и bus:

Частоты совместного появления слов в естественном языке «зашумляются» частыми словами типа артикля ‘the’ (закон Ципфа). Чтобы уменьшить этот эффект, вместо частоты будем использовать метрику pPMI (positive pointwise mutual information): $$ mathrm = max(0,,mathrm),

log frac

. $$ Если слова $w_1$ и $w_2$ «независимы», то условная вероятность $P(w_1,|,w_2)=P(w_1)$, а для совместной вероятности $P(w_1, w_2) ,=, P(w_1)P(w_2)$. В этом случае $mathrm=0$. Функция $max$ в определении pPMI обрезает нулевые значения совместных вероятностей и возможные отрицательные значения логарифма, если $P(w_1,|,w_2) docs (ROC историй) и составление словаря wordID описаны в документе ROC Stories.

Теперь можно вычислить векторы слов по формуле pPMI: Время получения компонент векторов для корпуса 100k ROCStories на Python занимает около минуты (при вычислениях на CPU Intel i7-7500U 2.7GHz, 16Gb). Приведём примеры нескольких компонент четырёх векторов (опуская нули):

Обратим внимание на малые значения pPMI с высокочастотными словами в последних колонках таблицы. Очевидно, что эти слова не имеют прямой смысловой связи со словами cat, dog, cat, bus.

Видео:Угол между векторами. 9 класс.Скачать

Понижение размерности

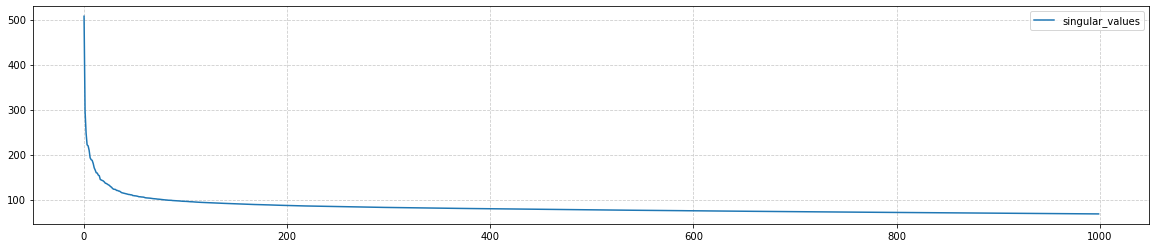
Хотя компоненты векторов слов теперь отражают сходство слов, их размерность так-же велика, как и при one-hot кодировке. Для понижения размерности эмбединга, воспользуемся методом главных компонент ( PCA: principal component analysis): Вычисление главных компонент для матрицы (10000, 10000) занимает около 7 минут. Первые 50 собственных значений ковариационной матрицы ( pca.singular_values_) быстро убывают, а потом убывание к нулю (при i=V) становится практически линейным:

Ограничимся далее размерностью векторного пространства E_DIM = E = 100: Финальная нормализация компонент (вычитание среднего и деление на разброс) переносит «центр облака точек» в начало координат, что улучшает работу косинусной меры расстояния (см. ниже). Деление на корень от размерности эмбединга E_DIM, масштабирует длины векторов в среднем к единичному значению.

Видео:Скалярное произведение векторов. 9 класс.Скачать

Меры близости

Меры близости двух векторов $mathbf$, $mathbf$ в многомерном пространстве можно выбрать различным образом: $$ begintext & text_1(mathbf,mathbf) &=& sqrt<(mathbf-mathbf)^2>\[2mm] text & text_2(mathbf,mathbf) &=& 1-cos(mathbf,mathbf)&=& 1-displaystyle frac<mathbfmathbf><|mathbf|cdot|mathbf|> end $$ После сокращения размерности чаще используют косинусное расстояние. При помощи косинусного расстояния найдём ближайших соседей к некоторым словам (см. модуль my_embedding.py):

• cat: kitten (0.17), dog (0.18), puppy (0.25), kittens (0.32), stray (0.33), pet (0.33), poodle (0.34), pup (0.36), chihuahua (0.36), shelter (0.37), meowed (0.37), cats (0.38), kitty (0.39)
• car: truck (0.23), vehicle (0.28), driving (0.30), cars (0.30), driver (0.32), road (0.33), intersection (0.33), interstate (0.33), tire (0.34), brakes (0.34), semi (0.34), towed (0.34), sped (0.35), highway (0.36), rear-ended (0.38), ford (0.39), van (0.39), swerved (0.39), wrecked (0.40), oncoming (0.40), drivers (0.41), parked (0.41)
• apple: orchard (0.30), peach (0.31), apples (0.32), blueberry (0.34), pie (0.34), fruit (0.37), cherry (0.37), banana (0.42), oranges (0.43), bakes (0.46), peaches (0.46), bake (0.48), dessert (0.48), ripe (0.48), fresh (0.49), smoothie (0.49), picking (0.49), grapes (0.49), pumpkin (0.49), pies (0.49), muffins (0.51), bananas (0.51), lemon (0.52), cherries (0.53)
• gin: vodka (0.27), martini (0.32), drink (0.32), drank (0.34), drinking (0.38), drinks (0.40), wine (0.40), iced (0.41), sipping (0.41), champagne (0.43), beer (0.43), bartender (0.45), whiskey (0.46), beers (0.47), alcoholic (0.48), espresso (0.49), decaf (0.49), sipped (0.49), soda (0.50), beverage (0.50), tea (0.50), sip (0.50), glass (0.51), coffee (0.51)
• monday: tuesday (0.39), saturday (0.47), early (0.48), wednesday (0.48), friday (0.50), overslept (0.50), thursday (0.51), morning (0.52), late (0.52), noon (0.54), sunday (0.55), meeting (0.55), today (0.55), pm (0.57), scheduled (0.57), :30 (0.58), appointment (0.59), 11 (0.60), lecture (0.61), postponed (0.62), woke (0.62), 8 (0.62), arrive (0.62), april (0.63)
• red: blue (0.23), yellow (0.29), bright (0.31), stripes (0.34), white (0.37), pale (0.38), purple (0.42), brown (0.42), pink (0.43), flashing (0.43), green (0.43), colored (0.44), resulting (0.47), black (0.47), puffy (0.48), orange (0.50), dyed (0.51), streaks (0.51), color (0.52), dye (0.53), eyes (0.53), stains (0.54), ink (0.54), stained (0.55)
• small: large (0.39), a (0.46), big (0.46), suburban (0.52), huge (0.54), tiny (0.55), near (0.58), breeder (0.59), stone (0.59), sized (0.60), cardboard (0.61), own (0.61), inheritance (0.62), corgi (0.64), larger (0.64), little (0.64), lived (0.65), isolated (0.66)
• say: [seem (0.43), tell (0.43), know (0.46), anything (0.46), understand (0.48), what (0.48), happen (0.49), exist (0.49), matter (0.50), psychic (0.50), saying (0.50), don’t (0.51), anybody (0.51), hello (0.51), why (0.52)’, won’t (0.52), god (0.52), cruel (0.54), hi (0.54), respond (0.54), says (0.55), ? (0.55), sorry (0.56), yes (0.56)

Для сравнения косинусное и евклидово расстояние между этими словами: Обратим внимание, что косинусное расстояние между словами из «разичных кластеров» порядка единицы, что говорит о перпендикулярности этих векторов.

По сравнению с подходами, основанными на нейронных сетях, векторизация при помощи на PCA достаточно быстрый метод и при относительно небольших словарях может служить очень неплохим первым приближением.

Видео:Векторное произведение векторовСкачать

Свойства векторного пространства

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Семантические направления

Видео:Лекция 18. Скалярное произведение векторов и его свойства.Скачать

Немного математики $^*$

Напомним, что метод PCA в $n$-мерном пространстве ищет «ближайшую» к обучающим точкам $m$-мерную плоскость, для которой средне-квадратичное отклонение расстояний множества точек минимально.
Kоординаты $N$ точек в $n$-мерном пространстве определяются матрицей $mathbf$ формы $(N,n)$. Пусть из координат вычтены их средние значения по всем точкам. Тогда ковариационная матрица равна $mathbf = mathbf^topmathbf/(N-1)$.

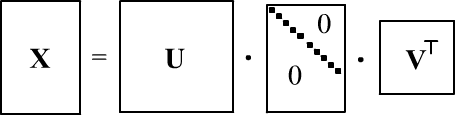
Решение PCA-задачи сводится к нахождению отсортированных в порядке убывания $lambda_1 ge . ge lambda_n$ собственных значений $lambda_alpha$ ковариационной матрицы: $mathbf,mathbf^=lambda_alpha,mathbf^.$ Пусть $mathbf=text(lambda_1. lambda_n)$ — диагональная матрица. Тогда $mathbf=mathbfmathbfmathbf^top$, где в каждой колонке матрицы $mathbf_=v^_i$ находятся компоненты собственных векторов $mathbf^.$ Первые $m$ колонок матрицы $mathbfmathbf$ формы $(N,n)$ будут координатами проекций точек $mathbf$ на $m$-мерную плоскость.

При нахождении $mathbf$, перемножение больших матриц $mathbf$ формы $(N,n)$ приводит к потери точности. Поэтому иногда эффективнее использовать SVD-разложение (singular value decomposition):

где $mathbf$ — диагональная матрица $(N,n)$ c сингулярными числами $s_i$ на диагонали, а $mathbf, mathbf$ — ортогональные матрицы (колонки $mathbf$ — собственные векторы матрицы $mathbfmathbf^top$, а колонки $mathbf$ — собственные векторы $mathbf^topmathbf$). Понятно, что

Таким образом, собственные значения ковариационной матрицы равны $lambda_i=s^2_i/(N-1)$, а главные компоненты даются произведением $mathbfmathbf=mathbfmathbfmathbf^topmathbf=mathbf,mathbf$. На numpy, PCA при помощи SVD делается следующим образом:

Видео:Векторное произведение двух векторовСкачать

Global Vectors (GloVe)

При очень больших словарях понижение размерности методом PCA или SVD может быть затруднительно. В этом случае, обычно, используют нейронные сети, которые сразу работают с векторными пространствами небольших измерений (см. следующий документ). В работе Pennington J. et.al. (2014) был предложен промежуточный подход, названный «Global Vectors for Word Representation» или сокращённо GloVe.

В этом подходе сначала вычисляются логарифмы вероятностей $P_$ совместной встречаемости слов $w_i$ и $w_j$ в тексте внутри скользящего окна из 10 слов. Подбираемыми параметрами модели являются компоненты E-мерных векторов $mathbf_i$ слов и параметры смещения $b_i$. В процессе обучения (подбора $mathbf_i$ и $b_i$) минимизируется следующий функционал ошибки:

$$ text = sum_ f(N_),bigr(mathbf_imathbf‘_j + b_i + b’_j — log P_bigr)^2 = min_<mathbf_i,mathbf‘_j,b_i,b’_j> $$ Веса $f(N_)$ пропорциональны числу появления $N_$ пары в окне. Эти веса обрезаются для слишком высокочастотных слов. Авторы выбрали следующую функцию, в которой $x_text=100$ независимо (?) от длины текста. 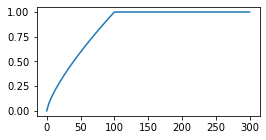$$ f(x) = left< begin (x/x_<text>)^ & text

x PMI, т.е. минимизируя ошибку мы стремимся получить что-то типа $mathbf_imathbf‘_j = log P_/P_i P_j$.

Векторизация была проведена на больших корпусах текстов:

We trained our model on five corpora of varying sizes: a 2010 Wikipedia dump with 1 billion tokens; a 2014 Wikipedia dump with 1.6 billion tokens; Gigaword 5 which has 4.3 billion tokens; the combination Gigaword5 + Wikipedia2014, which has 6 billion tokens; and on 42 billion tokens of web data, from Common Crawl

В открытом доступе находятся наборы векторов с размерностью от 50 до 300 и словарём 400k. Перед построением словаря, авторы «tokenize and lowercase each corpus with the Stanford tokenizer». Хорошей идей при использовании GloVe будет также использование Stanford tokenizer, т.к. он делает «непробельное» разбиение: can’t → [ca, n’t]; she’s → [she, ‘s] и т.п.

Анализ векторного пространства GloVe можно найти в этом документе.

Видео:89. Разложение вектора по двум неколлинеарным векторамСкачать

Проблемы эмбединга

Технология эмбединга — одно из самых замечательных изобретений последнего десятилетия. Однако, с ней связан также ряд проблем.

✑ Для получения надёжных контекстных векторов редких слова требуется очень большой корпус текстов. Однако, в большом корпусе может происходить перекос в семантических значениях слов по сравнению с их харатерными обыденными значениями. Например при векторизации GloVe для слова apple получаем следующих ближайших соседей: microsoft(.26), ibm (.32), intel(.32), software(.32), dell (.33). В тоже время существенно меньший корпус ROC Stories выдаёт более «обыденных соседей» для apple.

✑ Простой эмбединг не учитывает семантической и синтаксической неоднозначности. Обычно предполагается, что семантическая неоднозначность снимается, после прохождения исходных векторов слов через несколько слоёв нейронной сети, в которых анализируется контекст всего предложения (архитектуры RNN или Attention). Например, общий контекст предложений » Remove first row of the table.» и » Put an apple on the table» позволяет в каждом случае уточнить семантическое значение слова table.

✑ Так как слова в векторном пространстве являются точками, а не протяжёнными областями, эмбединг не отражает иерархической природы смыслов: предмет — инструмент — молоток.

💡 Видео

Разложение вектора по базису. 9 класс.Скачать

2 42 Ортогональность векторовСкачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

9 класс, 1 урок, Разложение вектора по двум неколлинеарным векторамСкачать

Геометрия 11 класс (Урок№2 - Скалярное произведение векторов.)Скачать

Два критерия коллинеарности и один критерий компланарности векторов.Скачать

Семинар 3 - Косинусное расстояние и близостьСкачать

Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

Что такое вектора? | Сущность Линейной Алгебры, глава 1Скачать