Медиана am треугольника abc продолжена

Математика | 5 — 9 классы

В треугольнике АВС медиана АМ продолжена за точку М до точки D на расстояние, равное АМ , так что АМ = МD.

Докажите, что АВСD — параллелограмм.

АМ = МD — по условию

ВМ = СМ — так как АМ — медиана

∠ВМА = ∠DМС как вертикальные

ΔАМВ = ΔDMC — по 1 — му признаку равенства треугольников

Следовательно, АВ = CD и ∠АВМ = ∠DCM — эти углы накрест лежащие при прямых АВ и CD и секущей ВС.

Если две стороны выпуклого четырёхугольника равны и параллельны, то этот четырёхугольник параллелограмм.

Что и требовалось доказать.

Видео:№231. Медиана AM треугольника ABC равна половине стороны ВС. Докажите, что треугольникСкачать

Внутри параллелограмма АВСD отмечена точка М?

Внутри параллелограмма АВСD отмечена точка М.

Докажите, что сумма площадей треугольников AMD и CMD равна половине площади параллелограмма ABCD.

Видео:№106. Медиана AD треугольника ABC продолжена за сторону ВС на отрезок DE, равный ADСкачать

Расстояния от точки пересечения медиан прямоугольного треугольника до вершин острых углов равны a, b?

Расстояния от точки пересечения медиан прямоугольного треугольника до вершин острых углов равны a, b.

Найти расстояние от этой точки до вершины прямого угла.

Пожалуйста помогите решить.

Видео:№115. Медиана AM треугольника ABC равна отрезку ВМ. Докажите, что один из углов треугольника ABCСкачать

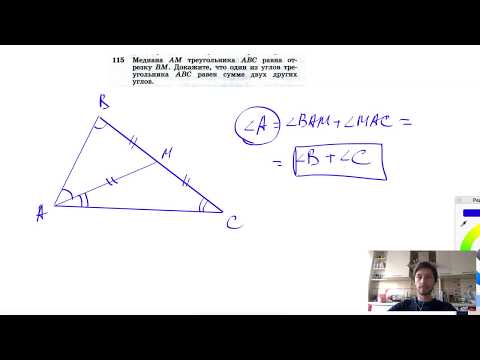
Площадь треугольника АВС равна Q?

Площадь треугольника АВС равна Q.

Найдите площадь треугольника АОВ1 , где О — точка пересечения медиан треугольника АВС, а В1 — середины стороны АС.

Видео:№109. В равнобедренном треугольнике ABC с основанием ВС проведена медиана AM. Найдите медиану AMСкачать

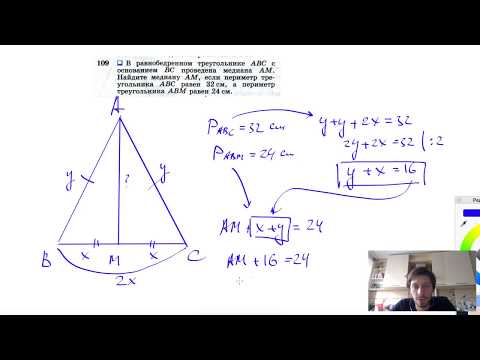
В параллелограмме АВСD точка К — середина стороны АD(боковой)?

В параллелограмме АВСD точка К — середина стороны АD(боковой).

Найдите площадь параллелограмма, если площадь треугольника DCK равна 5.

Видео:№942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать

Прямая, параллельная стороне АВ треугольника АВС, пересекает сторону АС в точке М, а сторону ВС — в точке К?

Прямая, параллельная стороне АВ треугольника АВС, пересекает сторону АС в точке М, а сторону ВС — в точке К.

Докажите, что углы треугольника МСК равны углам треугольника АВС.

Видео:Геометрия Медиана AM треугольника ABC равна m и образует со сторонами AB и AC углы α и βСкачать

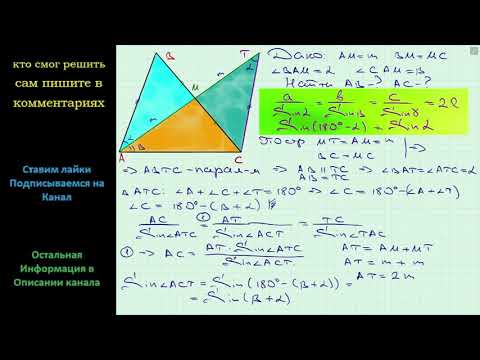
Прямая, параллельная стороне АВ треугольника АВС, пересекает сторону АС в точке М, а сторону ВС — в точке К?

Прямая, параллельная стороне АВ треугольника АВС, пересекает сторону АС в точке М, а сторону ВС — в точке К.

Докажите, что углы треугольника МСК равны углам треугольника АВС.

Видео:№161. В треугольниках ABC и А1B1С1 медианы AM и А1М1 равны, BC=B1С1 и ∠AMB=∠A1M1B1. Докажите, чтоСкачать

Сторона правильного треугольника АВС равняется 12 см?

Сторона правильного треугольника АВС равняется 12 см.

Точка S расположена на одинаковом расстоянии от каждой из вершин треугольника АВС и расстояние от точки S до плоскости треугольника АВС, = 4см.

Найдите расстояние от точки S до вершины треугольника ABC.

Видео:2.17.1. Планиметрия. Гордин Р.К.Скачать

Медианаа СД треугольника АВС равна 9 см?

Медианаа СД треугольника АВС равна 9 см.

Найдите отрезки СО и ОД, где О — точка пересечения медиан треугольника АВС Помогите приз, по действиям))).

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Медиана АМ треугольника АВС равна половине стороны ВС?

Медиана АМ треугольника АВС равна половине стороны ВС.

Докажите что треугольник АВС прямоугольный.

Видео:8. Медиана треугольника и её свойства.Скачать

Помогите решить задачу по геометрии?

Помогите решить задачу по геометрии.

В равнобедренный треугольник авс, аб = бс = 10, ас = 16.

Найдите расстояние между точками пересечения медиан и точкой пересечения биссектрис треугольника.

На этой странице находится вопрос В треугольнике АВС медиана АМ продолжена за точку М до точки D на расстояние, равное АМ , так что АМ = МD?, относящийся к категории Математика. По уровню сложности данный вопрос соответствует знаниям учащихся 5 — 9 классов. Здесь вы найдете правильный ответ, сможете обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С помощью автоматического поиска на этой же странице можно найти похожие вопросы и ответы на них в категории Математика. Если ответы вызывают сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.

506147 = 50000 + 6 + 100 + 40 + 7 38005 = 30000 + 80000 + 5 2005150 = 200 + 50 + 1 + 50 4004 = 4000 + 4.

500 000 + 6000 + 100 + 40 + 7 30000 + 8000 + 5 200000 + 100 + 50 4000 + 4.

110 — 54 = 56 56 / 7 = 8 Ответ 8 ящиков.

Для начала узнаем сколько моркови разложили по ящикам — 110 — 54 = 56 Потом мы узнаем кол — во ящиков — 56 : 7 = 8 Ящиков потребовалось.

1)f (x) = 4 2)f (x) = 4 / 2х 3)f (x) = 4 4)y = 8.

Ответ : 3 м израсходовано на один бант. Решение : сначала необходимо найти, сколько метров ленты израсходовано на упаковку подарков, для этого нужно всю длину ленты умножить на 1 / 10 : 1) 30 * 1 / 10 = 3 (м). Далее найдем, сколько ленты осталось, ..

15 * (53 — 8х) = 75 53 — 8х = 75 : 15 53 — 8х = 5 8х = 53 — 5 8х = 48 х = 48 : 8 х = 6.

13 ; 35 ; 57 ; 79 ; 97 ; 75 ; 53 ; 31 ; 15 ; 17 ; 19 ; 37 ; 39 ; 93 ; 73 ; 91 ; 71 ; 51 ; Ответ : 18.

Видео:№167. Стороны равностороннего треугольника ABC продолжены, как показано на рисунке 94, на равныеСкачать

Свойства медианы треугольника. Итоговое повторение курса геометрии 7 – 9 класса

Свойства медианы треугольника

Итоговое повторение курса геометрии 7 – 9 класса

При изучении какой-либо темы школьного курса можно отобрать определенный минимум задач, овладев методами решения которых, учащиеся будут в состоянии решить любую задачу на уровне программных требований по изучаемой теме. Предлагаю рассмотреть задачи, которые позволят увидеть взаимосвязи отдельных тем школьного курса математики. Поэтому составленная система задач является эффективным средством повторения, обобщения и систематизации учебного материала в ходе подготовки учащихся к экзамену.

Для сдачи экзамена не лишними будут дополнительные сведения о некоторых элементах треугольника. Рассмотрим свойства медианы треугольника и задачи, при решении которых этими свойствами можно воспользоваться. В предложенных задачах реализуется принцип уровневой дифференциации. Все задачи условно поделены на уровни (уровень указан в скобках после каждого задания).

Вспомним некоторые свойства медианы треугольника

Свойство 1. Докажите, что медиана треугольника ABC, проведённая из вершины A, меньше полусуммы сторон AB и AC.

Отложим на продолжении медианы AM за точку M отрезок MK, равный AM. Тогда в четырёхугольнике ABKC диагонали пересекаются и точкой пересечения делятся пополам. Значит, ABKC — параллелограмм. Применяя неравенство треугольника к треугольнику ABK, получим, что

то, сложив почленно эти три неравенства, получим, что

2AM + BN + CK > AB + BC + AC.

Отсюда следует, что AM + BN + CK > (AB + BC + AC).

Отложим на продолжении медианы AM за точку M отрезок MA1, равный AM. Тогда ABA1C — параллелограмм. Поэтому

BA1 = AC, 2AM = AA1 SDEF’ , то SAED+SBFD>SDEF , следовательно, указанным образом расположить точки невозможно.

так расположить точки нельзя.

Источник: Окружная олимпиада (Москва) , 2008 г, 11 класс

№32 Темы: Удвоение медианы. Ортоцентр и ортотреугольник Сложность:5 + Три точки, лежащие на одной прямой Подобные треугольники Классы: 9,10

В неравнобедренном треугольнике ABC точки H и M – точки пересечения высот и медиан соответственно. Через вершины A , B и C проведены прямые, перпендикулярные прямым AM , BM , CM соответственно. Докажите, что точка пересечения медиан треугольника, образованного проведенными прямыми, лежит на прямой MH .

Решение

Пусть A’B’C’ – треугольник, образованный

проведенными прямыми и G – точка пересечения его

медиан. Мы докажем, что M является серединой отрезка GH . Достроим треугольник BMC до параллелограмма BMCA1 . Отрезок MA1 делит сторону BC пополам, поэтому A1 лежит на прямой AM , причем AM = A1M (поскольку точка M делит медиану в отношении 2:1 ). Кроме того, BA1|| MC A’B’ и CA1|| MB A’C’ , поэтому BA1 и CA1 – высоты треугольника BA’C , значит A1 является ортоцентром треугольника BA’C , и

A’A1 BC . Стороны треугольника BA1M перпендикулярны

сторонам треугольника A’B’C’ соответственно, поэтому эти треугольники подобны, причем соответствующие прямые BC и

AG , содержащие медианы этих треугольников,

перпендикулярны. Значит, прямая A’G совпадает с прямой A’A1 . Пусть G’ – точка, симметричная точке H относительно M . Треугольники AHM и A1G’M симметричны относительно M , поэтому A1G’|| AH BC . Отсюда следует, что G’ лежит на прямой A’G . Аналогично, получаем, что G’ лежит на прямой B’G , то есть G’ совпадает с G .

Источник: Всероссийская олимпиада по математике, 2008 г, 9 класс

Отрабатываем умение: самостоятельно решать задачи.

Свойства медианы. Площадь треугольника

1. В треугольнике АВС медиана АМ перпендикулярна медиане BN. Найдите площадь треугольника АВС, если длина АМ равна 3, а длина BN равна 4.

2. Основание равнобедренного треугольника равно 2. Медианы, проведенные к боковым сторонам, взаимно перпендикулярны. Найдите площадь треугольника.

3. Две медианы равнобедренного треугольника взаимно перпендикулярны. Боковая сторона равна . Найдите площадь треугольника.

4. В треугольнике АВС медианы АD и ВE перпендикулярны, , . Чему равен квадрат третьей стороны?

5. Сторона треугольника равна 20, а медианы, проведенные к двум другим сторонам – 24 и 18. Найдите площадь треугольника.

6. Стороны треугольника равны 13, 14 и 15. Найти площади треугольников, на которые разбивается данный треугольник его медианами.

7. Площадь треугольника АВС равна 12. Из вершины тупого угла В проведена медиана BD, длина которой равна 3. Найдите длину стороны АС, если угол ABD – прямой.

8. Найдите площадь треугольника, если две его стороны равны 1 и , а медиана третьей стороны равна 2. (Указание – достроить до параллелограмма).

О т в е т: .

1. Одна сторона треугольника равна а, другая – b. Найдите третью сторону, если известно, что она равна медиане, проведенной к ней.

О т в е т: .

2. Основание равнобедренного треугольника , медиана боковой стороны 5. Найдите длины боковых сторон.

3. В равнобедренном треугольнике основание равно , а угол при основании равен 300. Найдите длину медианы, проведенной к боковой стороне.

4. Медианы треугольника равны 5, и . Докажите, что треугольник прямоугольный.

5. Числа , и выражают длины медиан некоторого треугольника. Докажите, что если выполняется равенство , то треугольник является прямоугольным.

Медиана, проведенная к гипотенузе

1. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна 3 см и делит прямой угол в отношении 2:1. Найдите меньший катет.

2. АА1, ВВ1, СС1 – медианы треугольника АВС. . Найдите .

3. Медианы треугольника АВС АА1, ВВ1 и СС1 пересекаются в точке О. .см. см. Найдите ВО.

4. Гипотенуза прямоугольного треугольника в 4 раза больше проведенной к ней высоты. Найдите острые углы треугольника.

О т в е т: 150; 750.

5. В трапеции ABCD углы при основании AD равны 200 и 700, длина отрезка, соединяющего середины оснований, равна 3. Найдите длину отрезка, соединяющего середины диагоналей трапеции.

· , , Ленинградские математические кружки

· , Задачи по планиметрии, Издательство МЦНМО, 2001г

· интернет сайт http://zadachi. ***** Задачи по геометрии

· Всероссийская олимпиада по математике, 2008 год,

· Турнир им. Ломоносова, 2001 год

· Московская математическая регата, 2012/13 г, 8 класс

Видео:Решали пол-урока, а оказалось очень простоСкачать

Сторона AB треугольника ABC продолжена на отрезок BP, равный AB, а медиана AM — на отрезок MQ, равный AM. Докажите, что BC = PQ.

Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Ваш ответ

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Похожие вопросы

• Все категории
• экономические 43,284
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,093
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

🎦 Видео

№786. Отрезки AA1, ВВ1 и СС1 — медианы треугольника ABC. Выразите векторы AA1, BB1, СС1Скачать

90 школьников решают эту задачу неправильно. Сможешь решить с помощью теоремы Пифагора?Скачать

В треугольнике ABC проведена медиана BM, на стороне AB взята точка K так, что AK = 1/3 AB. РЕШЕНИЕ!Скачать

№140. В треугольниках ABC и А1B1С1 медианы ВМ и B1М1 равны, АВ =А1B1, АС=А1С1. Докажите, что ΔABCСкачать