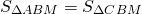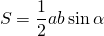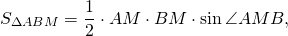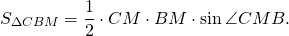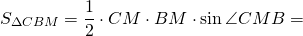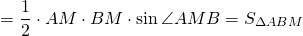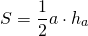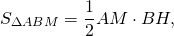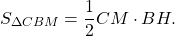Видео:Деление окружности на 3; 6; 12 равных частейСкачать
Медиана делит треугольник
Медиана делит треугольник на два равновеликих треугольника.
Равновеликие треугольники — это треугольники, имеющие равные площади.
То есть медиана делит исходный треугольник на два треугольника с равными площадями (или медиана делит площадь треугольника пополам).
Дано : ABC,
∠AMB +∠CMB=180º (как смежные).
Что и требовалось доказать.
Проведём высоту BH.
Так как AM=CM, то
Что и требовалось доказать.
Видео:Как поделить окружность на 3 равные части. Очень просто. Уроки черчения.Скачать
2 Comments
а можно попроще? без син, мы их не изучали
Alex, утверждение доказано двумя способами.
Видео:Как разделить угол на равные части с помощью циркуляСкачать
Медиана делит площадь треугольника пополам
Медиана делит площадь треугольника пополам
Два треугольника называются равновеликими. Если они имеют одинаковую площадь.
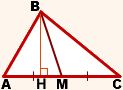
Теорема 1. Медиана делит треугольник на два равновеликих треугольника.
Пусть ВМ – медиана треугольника АВС. Докажем, что
.
Проведем высоту BH треугольника АВС. Тогда
,
.
Так как ВМ – медиана треугольника АВС, то АМ=МС, поэтому
.
,
.
Что и требовалось доказать.
Теорема 2. Медианы треугольника разбивают его на шесть равновеликих треугольников.
Доказательство можно посмотреть, например, в методическом пособии «Опорные задачи по планиметрии».
Из теоремы, в частности следует, что если точку пересечения медиан треугольника соединить со всеми его вершинами, то треугольник разобьется на три равновеликие части.
Задача 1 Две медианы треугольника взаимно перпендикулярны и равны соответственно 3 и 4. Найти площадь треугольника.
Пусть в треугольнике АВС медианы АМ и ВЕ равны 3 и 4 соответственно, 
, К – точка пересечения медиан.
,
.
Так как треугольник АВК прямоугольный с прямым углом ВКА, то 
.
Так как медиан делят треугольник на 6 равновеликих частей, то 
.
Задача 2 Медианы треугольника равны 6, 8 и 10, найти площадь треугольника.
Пусть медианы АM, BE и CD данного треугольника соответственно равны 6, 8 и 10, К – точка их пересечения. Отложим на продолжении луча ВЕ за точку Е отрезок EF=KE. Соединим точки С, F и A.
Рассмотрим треугольник KAF.
,
то 
.
Далее, 
, так как CKAE – параллелограмм (по признаку параллелограмма: ели диагонали четырехугольника делятся точкой пересечения пополам, до данный четырехугольник параллелограмм), получаем 
.
Так как 
, то есть 
, то по обратной теореме Пифагора (если квадрат одной стороны треугольника равен сумме квадратов двух других его сторон, то треугольник прямоугольный) треугольник KAF – прямоугольный и 
.
Вычислим площадь треугольника AKF:
.
Теперь сравним площади треугольников AKF и АВС: так как AE – медиана треугольника AKF, то
, 
,
.
.
Отметим, что задачу можно решить по-другому, если воспользоваться тем фактом, что:
площадь треугольника, образованного медианами данного треугольника составляет 
от площади самого треугольника.
Доказательство можно посмотреть, например, в методическом пособии «Опорные задачи по планиметрии».
Вопросы для самопроверки:
1. Какие треугольники называются равновеликими?
2. Площадь треугольника равна S. Чему равна площадь каждого из треугольников, на которые его разбивает медиана, проведенная к какой-либо стороне этого треугольника?
3. На сколько равновеликих частей разбивают треугольник проведенные в нем три медианы?
4. Площадь треугольника равна S. Цент тяжести этого треугольника соединили с его вершинами. Чему равна площадь каждого из получившихся треугольников?
5. Площадь треугольника равна 48, чему равна площадь треугольника, составленного из медиан этого треугольника?
6. Площадь треугольника, составленного из медиан некоторого треугольника равна 24, чему равна площадь треугольника?
Задачи для самостоятельного решения:
1. Две медианы треугольника взаимно перпендикулярны и равны соответственно 6 и 8. Найти площадь треугольника.
2. Медианы треугольника равны 3, 4 и 5 найти площадь треугольника.
3. Треугольник АВС, стороны которого 13 см, 14 см и 15 см, разбит на три треугольника отрезками, соединяющими точку М пересечения медиан треугольника с вершинами треугольника. Найти площадь треугольника ВМС.
4. Две стороны треугольника равны 10 и 12, а медиана, проведённая к третьей, равна 5. Найдите площадь треугольника.
Видео:Деление отрезка пополамСкачать
Как разделить треугольник пополам
Как разделить треугольник пополам — Рецепты
Видео:ДЕЛЕНИЕ ОТРЕЗКА НА РАВНЫЕ ЧАСТИ 396 Атанасян 8 классСкачать
Содержание
Треугольник — это трехсторонняя двумерная форма. Треугольники и их углы составляют основу большинства основных геометрических расчетов. Однако для того, чтобы научиться делить треугольник пополам или делить его на две части равной площади, не требуется никаких математических формул или сложных вычислений. Вам даже не нужно знать его площадь, чтобы разрезать его пополам. Хотя существуют более сложные способы разделить треугольник на две равные части, в этом руководстве мы сосредоточимся на самых простых.
Измерьте одну сторону треугольника. Неважно, какую сторону вы выберете.
Отметьте середину этой стороны. Чтобы найти середину, разделите длину стороны на 2, затем измерьте это расстояние. Например, если длина выбранной вами стороны составляет 6 дюймов, разделите 6 на 2. Когда вы нырнули 6 на 2, вы получите 3, так что середина стороны будет на 3 дюйма от обоих концов. Отмерьте 3 дюйма с одного конца стороны и отметьте эту точку.
Проведите линию под противоположным углом к только что сделанной отметке в средней точке. Проведите по линейке, чтобы линия получилась прямой. Вы только что разделили треугольник пополам. Несмотря на то, что вы никогда не вычисляли площадь треугольника, площадь с каждой стороны вашей линии будет одинаковой.
подсказки
Чтобы вычислить площадь треугольника, умножьте основание (измеренную вами линию) на высоту (нарисованную вами линию), а затем разделите результат на 2.
📽️ Видео
🧭Как разделить круг на ТРИ Части, без Линейки и Циркуля; How to split a circle into three partsСкачать
ДЕЛЕНИЕ УГЛА ПОПОЛАМ. 2 СПОСОБАСкачать
Как разделить окружность на 3 равные части или как вписать равнобедренный треугольник в окружностьСкачать
Деление отрезка на равные части, перпендикуляр к прямой.Урок 4.(Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать
Деление окружности на 3, 4, 5, 6 и 7 равных частейСкачать
Деление отрезка на 2,4,8 равных частей с помощью циркуля и линейкиСкачать
Как разделить круг на равные частиСкачать
Excel: Диагональное разделение ячейки (два заголовка в одной ячейке)Скачать
Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать
Построение биссектрисы углаСкачать
Построение пятиугольника циркулемСкачать
Деление отрезка циркулем на три части. How to divide a given segment into three parts by a compass.Скачать
Деление угла на равные части. Урок 5. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать
Строим прямой уголСкачать
Построение медианы в треугольникеСкачать
