Материальная точка м движется по окружности с убывающей (2 видео)

Определение сил по заданному движению

ДИНАМИКА ТОЧКИ

Определение сил по заданному движению

13.1.1Точка массой m=4 кгдвижется по горизонтальной прямой с ускорениемa=0,3t. Определить модуль силы, действующей на точку в направлении ее движения в момент времени t=3c. (3.6) Решение:Зная массу и ее ускорение, можно определить действующую на точку силу, в момент времени t=3c , ускорение будет

Материальная точка м движется по окружности с убывающей

тогда

13.1.2Ускорение движения точки массой m=27кгпо прямой задано графиком функции a=а(t). Определить модуль равнодействующей сил, приложенных к точке в момент времени t=5c. (4,05) Решение:Из графика видно что при t=5c , ускорение а=0,15м/с 2 , тогда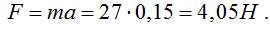

13.1.3 Деталь массой m=0,5кг скользит вниз по лотку. Под каким углом к горизонтальной плоскости должен располагаться лоток, для того чтобы деталь двигалась с ускорением а=2 м/с 2 ? Угол выразить в градусах. (11,8) Решение:Деталь движется под силой тяжести G=mg, сила под которой она движется по

лотку с некоторым углом а,

13.1.4Точка массой m=14кгдвижется по горизонтальной оси Ох с ускорениема_х.=lnt Определить модуль силы, действующей на точку в направлении движения в момент времени t=5c. (22,5) Решение:

13.1.5Трактор, двигаясь с ускорением а=1м/с 2 по горизонтальному участку пути, перемещает нагруженные сани массой 600кг. Определить силу тяги на крюке, если коэффициент трения скольжения саней f=0,04. (835) Решение:Необходимая сила тяги на крюке для перемещения саней с заданным ускорением 1м/с 2 :

13.1.6Тело массой m=50 кг, подвешенное на тросе, поднимается вертикально с ускорением а=0,5м/с 2 . Определить силу натяжения троса.(516) Решение:

13.1.7 Скорость движения точки m=24кг по прямой задана графиком функцииv=v(t). Определить модуль равнодействующей сил, действующих на точку. (36) Решение: из графика функции v=v(t) видно, что точка движется равноускоренно с ускорением а=1,5м/с, тогда равнодействующая сил

13.1.8 Материальная точка массой m=12кгдвижется по прямой со скоростьюv=е 0,1t . Определить модуль равнодействующей сил, действующих на точку в момент времени t=50c.(178) Решение:

13.1.9 Определить модуль равнодействующей сил, действующих на материльную точку массой m=3кг в момент времени t=6c, если она движется по оси Ох согласно уравнению х=0,04t 3 . (4,32) Решение:Ускорение точки найдем из уравнения движения (вторая производная по времени):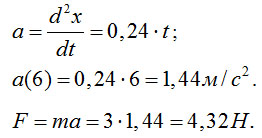

13.1.10 Материальная точка массой 1,4кг движется прямолинейно по законух=6t 2 +6t+3 . Определить модуль равнодействующей сил, приложенных к точке.(16,8) Решение:

Определение сил по заданному движению

Содержание

Кинематика поступательного движения
Материальная точка движется по окружности радиуса 1 м согласно уравнению s = 8t – 0,2t3. Найти скорость, тангенциальное, нормальное и полное ускорение в момент времени 3 с.
Описание и исходные данные задания, 50% решения + фотография:
📸 Видео

Видео:Материальная точка равномерно движется по окружности, центр которой находится в начале O - №22689Скачать

Кинематика поступательного движения

Автомобиль движется с постоянной по модулю скоростью по траектории, представленной на рисунке. В какой из указанных точек траектории центростремительное ускорение максимально?

#1 #2 #3 #Во всех точках одинаково

Точка М движется по спирали в направлении, указанном стрелкой. Нормальное ускорение по величине не изменяется. При этом величина скорости …

# уменьшается # увеличивается # не изменяется

Точка М движется по спирали с постоянной по величине скоростью в направлении, указанном стрелкой. При этом величина нормального ускорения …

# уменьшается # увеличивается # не изменяется

# увеличивается # уменьшается # не изменяется

Точка М движется по окружности с постоянным тангенциальным ускорением. Если проекция тангенциального ускорения на направление скорости положительна, то величина нормального ускорения…

# увеличивается # уменьшается # не изменяется

Точка М движется по окружности с постоянным тангенциальным ускорением. Если проекция тангенциального ускорения на направление скорости отрицательна, то величина нормального ускорения…

# уменьшается # увеличивается # не изменяется

Материальная точка M движется по окружности со скоростью . На рис. 1 показан график зависимости V_τ от времени ( – единичный вектор положительного направления, V_τ – проекция на это направление). На рис. 2 укажите направление ускорения т.М в момент времени t₂.

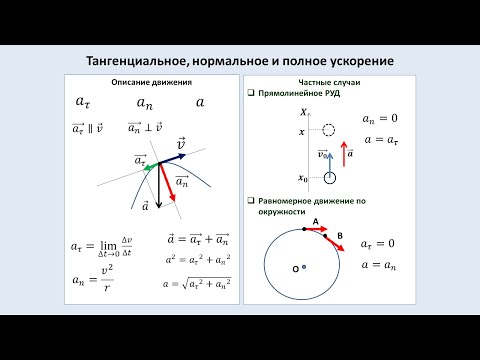
Если a_t и a_n – тангенциальная и нормальная составляющие ускорения, то для равномерного движения по окружности справедливы соотношения:

Если a_t и a_n – тангенциальная и нормальная составляющие ускорения, то соотношения: a_t = a = const, a_n = 0 справедливы для.

#прямолинейного равноускоренного движения #прямолинейного равномерного движения #равномерного криволинейного движения #равномерного движения по окружности

Если a_t и a_n – тангенциальная и нормальная составляющие ускорения, то соотношения: a_t = 0, a_n = const справедливы для.

#равномерного криволинейного движения #прямолинейного равноускоренного движения #прямолинейного равномерного движения #равномерного движения по окружности

Два тела брошены под одним и тем же углом к горизонту с начальными скоростями V₀и 2V₀. Если сопротивлением воздуха пренебречь, то соотношение дальностей полета S₂/S₁ равно .

Материальная точка М движется по окружности со скоростью . На рис. 1 показан график зависимости проекции скорости от времени ( – единичный вектор положительного направления, – проекция на это направление). При этом для нормального a_n и тангенциального a_t ускорения выполняются условия.

# – увеличивается, – постоянно # – постоянно, – увеличивается # – увеличивается, – увеличивается # – постоянно, – постоянно

Камень бросили под углом к горизонту соскоростью V₀. Его траектория в однородном поле тяжести изображена на рисунке. Сопротивления воздуха нет.

Модуль тангенциального ускорения a_t на участке А-В-С…

# увеличится # не изменяется # уменьшается

Автомобиль движется с постоянной по величине скоростью по траектории, представленной на рисунке. В какой из указанных точек траектории полное ускорение минимально?

#1 #2 #3 #Во всех точках одинаково

Тело брошено с поверхности Земли со скоростью 20 м/с под углом 45° к горизонту. Определите радиус кривизны его траектории в верхней точке. Сопротивлением воздуха пренебречь. (g = 10 м/с 2 ).

#10 м #20 м #30 м #80 м

Графики зависимости величины тангенциального ускорения от времени для равномерного движения тела по окружности изображен на рисунке.

# # # #

Точка М движется по спирали с постоянным по величине нормальным ускорением в направлении, указанном стрелкой. При этом проекция тангенциального ускорения на направление скорости .

#равна нулю #меньше нуля #больше нуля

# > 0; = 0 # = 0; 0; > 0 # > 0; a_B # a_A = a_B = 0 # a_A = a_B ≠ 0.

Тело брошено с поверхности Земли со скоростью 20 м/с под углом 60° к горизонту. Определите радиус кривизны его траектории в верхней точке. Сопротивлением воздуха пренебречь. (g = 10 м/с 2 ).

#10 м #20 м #30 м #80 м

Материальная точка движется по окружности. На чертеже изображена зависимость ее скорости от времени. Точка имеет наибольшее тангенциальное ускорение в момент времени .

Тело брошено под углом к горизонту и движется в поле силы тяжести Земли. На рисунке изображен восходящий участок траектории данного тела.

Правильно изображает полное ускорение вектор .

Тело брошено с поверхности Земли со скоростью 20 м/с под углом 30° к горизонту. Определите радиус кривизны его траектории в верхней точке. Сопротивлением воздуха пренебречь. (g = 10 м/с 2 ).

#10 м #20 м #30 м #80 м

Тангенциальное ускорение точки меняется согласно графику.

Такому движению соответствует зависимость скорости от времени .

# # # # .

Видео:Физика - движение по окружностиСкачать

Материальная точка движется по окружности радиуса 1 м согласно уравнению s = 8t – 0,2t3. Найти скорость, тангенциальное, нормальное и полное ускорение в момент времени 3 с.

Готовое решение: Заказ №8342

Тип работы: Задача

Статус: Выполнен (Зачтена преподавателем ВУЗа)

Предмет: Физика

Дата выполнения: 18.08.2020

Цена: 209 руб.

Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

№1 КР 1. Задача 9. Материальная точка движется по окружности радиуса 1 м согласно уравнению s = 8t – 0,2t3. Найти скорость, тангенциальное, нормальное и полное ускорение в момент времени 3 с.

Найдём закон изменения скорости точки: . Вычислим скорость точки в заданный момент времени: м/с. Найдём закон изменения тангенциального ускорения точки: (знак «минус» говорит о том, что точка замедляется). Вычислим тангенциальное ускорение точки в заданный момент времени: м/с2. Найдём закон изменения нормального ускорения точки:

Если вам нужно решить физику, тогда нажмите ➔ заказать физику.

Похожие готовые решения:

Материальная точка движется по окружности радиуса R = 2 м согласно уравнению s = 8t – 0,2t3 (длина – в метрах, время – в секундах). Найти скорость v, тангенциальное at, нормальное an ускорения в момент времени t = 3 с. Условие 2 51. Материальная точка массой 1 г движется по окружности радиуса 2 м согласно уравнению s = 8t – 0,2t3. Найти скорость, тангенциальное, нормальное и полное ускорения в момент времени 3 с.
Материальная точка движется по окружности радиуса R = 2 м согласно уравнению s = At +Bt3, где A = 8 м/с, B = – 0,2 м/с3. Найти скорость v, тангенциальное at, нормальное an и полное a ускорения в момент времени t = 3 с.
Определите максимальное значение скорости автомобиля при движении на повороте по дуге окружности радиусом 50 м, если максимальное значение коэффициента трения покоя шин на шоссе равно 0,4.
С какой наибольшей скоростью может двигаться автомобиль на повороте радиусом R, чтобы не возникло проскальзывание? Коэффициент сцепления колес автомобиля с землёй u. R = 12 м, u = 0,75.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.