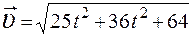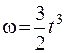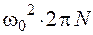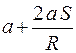Угловое движение можно условно разделить на два вида:
- Когда изменяется только направление вектора линейной скорости, а его длина не изменяется.
- Или, когда изменяются обе характеристики вектора линейной скорости.
Во втором случае, для описания движения будем применять более сложные формулы кинематики. Так как появится еще один вид ускорения.
Центростремительное (нормальное) ускорение есть всегда, когда есть движение по окружности, при этом не важно, меняется ли скорость тела по модулю, или не меняется.
- Движение по окружности с постоянной по модулю скоростью
- Тангенциальное ускорение – когда модуль скорости меняется
- Равноускоренное движение по окружности
- Равнозамедленное движение по окружности
- Общее ускорение при движении по окружности
- Кинематика поступательного и вращательного движения
- Перечень ответов тестовых заданий по разделу Физические основы механики. Статистическая физика и термодинамика дисциплины Физика — файл n1.doc
- n1.doc
- 🎬 Видео
Видео:Физика - движение по окружностиСкачать

Движение по окружности с постоянной по модулю скоростью
Пусть тело движется по окружности, но при этом длина вектора линейной скорости не меняется (рис. 1).
[left|vec right| = const]
На рисунке 1 указаны: а) – вид сбоку, б) вид сверху, вектор угловой скорости направлен к нам перпендикулярно рисунку.
Скорость будет меняться только по направлению от точки к точке, потому, что на тело действует центростремительная сила (displaystyle vec<F_<text>>) , тело обладает центростремительным (displaystyle vec<a_<text>>) (нормальным) ускорением.
Кроме линейной, тело обладает угловой скоростью. Если линейная скорость не изменяется по модулю, то длина вектора угловой скорости не меняется.
На рисунке 1а изображен вектор угловой скорости (displaystyle vec), на рисунке 1б вектор угловой скорости направлен к нам перпендикулярно плоскости рисунка. Направление, в котором тело движется по окружности, указано синей стрелкой.
Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Тангенциальное ускорение – когда модуль скорости меняется
Тело может увеличивать или уменьшать свою скорость, когда движется по окружности.
В таком случае, дополнительно к нормальному ускорению возникает тангенциальное (displaystyle vec<a_>) ускорение.
Тангенциальное ускорение играет роль линейного ускорения при прямолинейном движении тела. Вектор (displaystyle vec<a_>) направлен параллельно вектору (displaystyle vec) скорости.
Подобно движению по прямой, вектор ускорения – это первая производная скорости по времени, или вторая производная перемещения по времени.
Когда векторы скорости (vec) и ускорения (vec<a_>) сонаправлены (рис. 2), линейная и угловая скорости возрастают.
А когда ускорение (vec<a_>) направлено противоположно (рис. 3) вектору скорости (vec), угловая и линейная скорости уменьшаются.
С линейной скоростью (vec) связана угловая (vec) скорость.
Из рисунков 2, 3 следует: когда появляется тангенциальное ускорение, меняется и угловая скорость. Значит, тангенциальное ускорение (vec<a_>) появляется совместно с угловым (vec) ускорением и между ними есть связь.
Связь между тангенциальным и угловым ускорением выглядит аналогично связи между линейной и угловой скоростью.
В векторном виде
В скалярном виде
[ large boxed < a_= beta cdot R >]
(displaystyle vec left( frac<text><c^>right)) – угловое ускорение;
(displaystyle vec< a_> left( frac<text><c^>right)) – тангенциальное ускорение;
(R left( textright)) – радиус окружности.
Видео:Движение материальной точки по окружности | Физика ЕГЭ, ЦТСкачать

Равноускоренное движение по окружности
Угловая скорость увеличивается (рис. 2), когда угловое ускорение сонаправлено с вектором угловой скорости. Когда движение происходит с постоянным ускорением, его называют равноускоренным.
Для решения задач на равноускоренное движение по окружности, поступаем аналогично равноускоренному движению по прямой. Применяем систему из двух уравнений:
[ large boxed < beginomega = omega _ + beta cdot t \ displaystyle varphi = omega_ cdot t + beta cdot frac end > ]
Первое уравнение системы – это связь между начальной (omega_ ) и конечной (omega ) скоростью. Второе уравнение – это уравнение движения.
Видео:Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Равнозамедленное движение по окружности
Когда векторы (vec) и (vec) направлены в противоположные стороны, угловая скорость (vec) уменьшается (рис. 3).
Для решения задач кинематики, в которых угловая скорость уменьшается и, движение равнозамедленное, используем систему, состоящую из таких уравнений:
[ large boxed < beginomega = omega _ — beta cdot t \ displaystyle varphi = omega_ cdot t — beta cdot frac end > ]
Видео:Точка движется по окружности радиусом R=2см. Волькенштейн 1.47Скачать

Общее ускорение при движении по окружности
Пусть точка движется по окружности и линейная (vec) скорость ее изменяется по модулю. При этом, точка обладает двумя видами ускорения — нормальным и тангенциальным. Эти виды ускорения обозначают символом (vec).
Примечание: Любое ускорение, обозначаемое символом «a», измеряется в метрах, деленных на секунду в квадрате.
Направление вектора общего ускорения указано на рисунке 4а, а для равнозамедленного – на рисунке 4б.
Так как векторы (vec<a_>) и (vec<a_>) всегда перпендикулярны, длину вектора общего ускорения (vec) можно найти из теоремы Пифагора:
Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Кинематика поступательного и вращательного движения
Содержание
1. Кинематика поступательного и вращательного движения. 5
2. Динамика поступательного и вращательного движений. 11
3. Механические колебания и волны. 21
4. Молекулярная физика и термодинамика. 31
ВВЕДЕНИЕ
В сборнике представлены тестовые задания закрытого типа и на соответствие по разделу «Физические основы механики. Молекулярная физика и термодинамика» дисциплины «Физика», предназначенные для аудиторной и внеаудиторной самостоятельной работы студентов.
Тестовые задания сгруппированы по темам «Кинематика поступательного и вращательного движения», «Динамика поступательного и вращательного движений», «Механические колебания и волны», «Молекулярная физика и термодинамика».
Содержание тестовых заданий направлено на формирование у студентов знания физических явлений, законов, формул, единиц измерения физических величин, умения применять законы и формулы для решения качественных и расчетных задач, графически представлять физические явления и законы, анализировать их.
В тестовых заданиях закрытой формы из 3-5 приведенных ответов следует выбрать правильный. В заданиях на соответствие необходимо установить соответствие элементов одного множества элементам другого. Тестовые задания такой формы сопровождаются инструкцией «Установить соответствие».
Самостоятельная работа студентов с тестовыми заданиями поможет при подготовке к лабораторным и практическим занятиям, а также будет способствовать более глубокому изучению раздела дисциплины «Физика» «Физические основы механики. Молекулярная физика и термодинамика».
Кинематика поступательного и вращательного движения
1.Материальная точка движения так, что радиус-вектор меняется со временем по закону 

1. 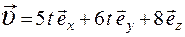
3. 
5.
2.Материальная точка движется согласно уравнению 
1. 48 2. 24 3. 5 4. 2 5. 0
3.Радиус-вектор частицы определяется выражением 
1. 707 2. 500 3. 150 4. 100 5. 25
4.Частица за некоторое время прошла 3/4 окружности со средним значением модуля скорости 

1. 



5.Радиус-вектор частицы изменяется со временем по закону 
1. 14 2. 8 3. 8,8 4. 12,6 5. 10
6.Вектор средней скорости материальной точки совпадает по направлению с
1. радиус-вектором, определяющим положение точки
2. вектором полного ускорения
3. вектором нормального ускорения
4. касательной к траектории
5. вектором перемещения
7.Частица движется со скоростью 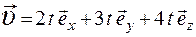
1. 13,5 2. 5,38 3. 24,3 4. 27 5. 9
 |
8.Зависимость скорости движения материальной точки по прямой от времени дана на рисунке. Среднее значение модуля скорости движения материальной точки в интервале времени 0-5 с равна (м/с)
1. 1,5 2. 0,25 3. 2,5 4. 0,2 5. 1,4
 |
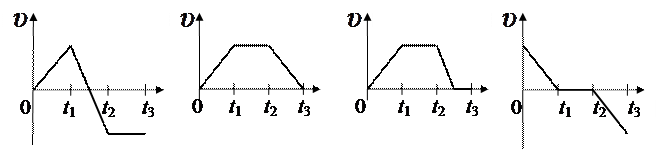
9.На рисунке приведен график зависимости ускорения тела от времени
График зависимости скорости тела от времени имеет вид
1. а 2. б 3. в 4. г

Зависимость пути, пройденного телом, от времени, представлена на графике
1. а 2. б 3. в 4. г
11. От движущегося поезда отцепляют последний вагон, который вследствие трения останавливается, а поезд продолжает двигаться с прежней скоростью 
1. 2 2. 4 3. 1 4. 0,5 5. 0,1
12.Две материальные точки движутся согласно уравнениям 
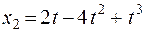
1. 0,23 2. 0,542 3. 0,845 4. 0,9 5. 1
13. Тело брошено с начальной скоростью 
1. 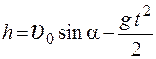
3. 

14.Тело брошено под углом α к горизонту. Чтобы максимальная высота подъема тела была равна дальности полета, угол α должен быть равен (град)
1. 30 2. 60 3. 45 4. 76 5. 84
15.Тело брошено под углом α к горизонту с начальной скоростью 
1. 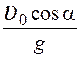

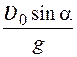



16.Тело брошено под углом α к горизонту с начальной скоростью 

1. 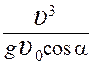
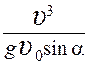


17.Мяч брошен под углом 60° к горизонту с начальной скоростью 10 м/с. Модуль скорости мяча через 0,2 с после броска равен (м/с)
1. 2 2. 8,3 3. 8,7 4. 9,2 5. 12,8
18.С вышки бросили камень в горизонтальном направлении. Через 2 с камень упал на землю на расстоянии 40 м от основания вышки. Конечная скорость камня равна (м/с)
1. 20 2. 28,3 3. 23 4. 40 5. 17,3
19.Тело брошено с высоты с горизонтальной скоростью 

1. 40 2. 20 3. 5 4. 2,5 5. 1
20.Два бумажных диска (расстояние между ними 30 см), насаженные на общую горизонтальную ось, вращаются с угловой скоростью 2000 об/мин. Пуля, летящая горизонтально на расстоянии 12 см от оси, пробивает оба диска, причем пробоина во втором диске смещена по сравнению с первым на 6 см (по дуге окружности). Средняя скорость пули в промежутке между дисками равна (м)
1. 500 2. 250 3. 126 4. 105 5. 65
21.Материальная точка движется равноускоренно по окружности, лежащей в горизонтальной плоскости, по часовой стрелке. Вектор угловой скорости направлен
1. по касательной
2. вдоль радиуса окружности
3. вниз по оси вращения
4. вверх по оси вращения
5. среди ответов 1- 4 нет верного
22.Материальная точка движется равнозамедленно по горизонтальной окружности против часовой стрелки. Вектор углового ускорения направлен по
1. касательной к окружности
2. радиусу окружности
3. оси вращения вверх
4. оси вращения вниз
5. направлению угловой скорости
23.Материальная точка вращается в горизонтальной плоскости относительно неподвижной оси с угловым ускорением ε = 2t 2 . При t = 0, ω0 = 0. Закон изменения угловой скорости имеет вид
1. 



24.Точка вращается по окружности радиуса R согласно уравнению 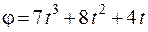
1. 
3. 

25.Точка вращается по окружности радиуса R согласно уравнению 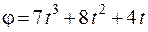
1. 
3. 
5.
26.Диск радиуса 10 см вращается согласно уравнению 
1. 3,54 2. 54,2 3. 2,4 4. 67,6 5. 26
27.Закон изменения угла поворота 

1. 19; 56 2. 56; 46 3. 88; 56 4. 86; 19 5. 76; 29
28.Закон изменения угловой скорости материальной точки имеет вид 
1. 




29.Маховик, вращавшийся с угловой скоростью 
1. 



30.Шкив с радиусом R вращается под действием груза, подвешенного на нити. Ускорение груза а. В момент, когда груз прошел расстояние S, полное ускорение произвольной точки на ободе шкива определяется выражением
1. 

4. 
Видео:Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать

Перечень ответов тестовых заданий по разделу Физические основы механики. Статистическая физика и термодинамика дисциплины Физика — файл n1.doc
приобрести
Перечень ответов тестовых заданий по разделу Физические основы механики. Статистическая физика и термодинамика дисциплины Физика
скачать (2893.5 kb.)
Доступные файлы (1):
| n1.doc | 2894kb. | 01.06.2012 14:54 | скачать |
Видео:Центростремительное ускорение. 9 класс.Скачать

n1.doc
«УТВЕРЖДАЮ»
Студент Икт-103
Несколько бессонных ночей, январь 2012 г.
Перечень тестовых заданий
по разделу «Физические основы механики. Статистическая физика и термодинамика» дисциплины «Физика»
Тестовые задания
Кинематика поступательного и вращательного движения материальной точки
1. Материальная точка движется равноускоренно по криволинейной траектории. Вектор мгновенной скорости направлен …
1. к центру кривизны траектории
2. по направлению вектора перемещения
3. вдоль радиуса кривизны от центра
4. по касательной к траектории
5. противоположно вектору ускорения
2. Вектор средней скорости материальной точки совпадает по направлению с …
1. радиус-вектором, определяющим положение точки
2. вектором полного ускорения
3. вектором нормального ускорения
4. касательной к траектории
5. вектором перемещения
3. Материальная точка движется по окружности радиуса R с периодом Т . Модуль вектора средней скорости за четверть оборота равен …
1. 




4. Материальная точка двигается равномерно по окружности со скоростью ? и за некоторое время прошла 3/4 окружности. Модуль вектора средней скорости частицы за это время равен …
1. 



5. Материальная точка двигается равномерно по окружности со скоростью 
1. 0 2. 




6. Зависимость проекции скорости движения материальной точки по прямой от времени дана на рисунке. Перемещение материальной точки за 5 с, равно …м.
7
1. 1,5 2. 0,25 3. 2,5
8. Поезд движется на подъеме со скоростью 

1. 




9. Радиус-вектор частицы, определяется выражением 
C = 7 м). Путь, пройденный частицей за первые 10 с движения, равен … м.
1. 25 2. 100 3. 150 4. 500 5. 707
10. Радиус вектор точки изменяется со временем по закону 
В= 1 м/c 2 , C = 1 м/c.. Скорость ? точки в момент t = 2 c по модулю равна … м/с.
1. 29,0 2. 26,0 3. 24,1 4. 24,3 5. 12,2
11. Радиус-вектор частицы изменяется со временем по закону 

1. 14 2. 8 3. 8,8 4. 12,6 5.10
12. Материальная точка движется так, что радиус-вектор меняется со временем по закону 

1. 

4. 
13. Радиус-вектор частицы изменяется во времени по закону 
14. Материальная точка движется согласно уравнению 

1. 48 2. 24 3. 5 4. 3 5. 8
15. Из точек А и В навстречу друг другу движутся два тела. Уравнения движения тел имеют вид: 

1. 11,2 2. 10 3. 7,8 4. 5,6 5. 5
16. Две материальные точки движутся согласно уравнениям: 

1. 0,54 2. 0,65 3. 0,74 4. 0,82 5. 0,94
17. Две материальные точки движутся согласно уравнениям: 

1. 0,23 2. 0,542 3. 0,845 4. 0,9 5. 1
18. Зависимость пройденного телом пути от времени дается уравнением S = At+Bt 2 (A = 2 м/с, В = 1 м/с 2 ). Средняя скорость тела за вторую секунду его движения равна … м/с.
1. 5 2. 5,5 3. 6 4. 7 5. 11
19. Тело начинает двигаться из состояния покоя с постоянным ускорением 2 см/с 2 . За третью секунду своего движения оно пройдет путь … см.
1.2 2. 3 3. 4 4. 5 5. 9
20. Вертолет поднимается вертикально вверх со скоростью 10 м/с. На высоте 100 м из него выбрасывается вверх предмет со скоростью 2 м/с относительно вертолета. Предмет упадет на землю через …с. (
1. 4,5 2. 5,3 3. 5,6 4. 5,8 5. 6,0
21. Камень падает с высоты 

1. 150 2. 300 3. 450 4. 600 5. 1050
22. Материальная точка начинает двигаться вдоль прямой так, что её ускорение прямо пропорционально квадрату времени (

1. 



23. Из одной и той же точки с интервалом 2 с брошены вертикально вверх два шарика с одинаковой скоростью 30 м/с. Они столкнуться (
1. 1 2. 2 3. 3 4. 4 5. 5
24. Мяч брошен под углом 60є к горизонту с начальной скоростью 10 м/с. Скорость мяча через 0,2 с после броска равна … м/с.
1. 2 2. 8,3 3. 8,7 4. 9,2 5. 12,8
25. Два тела брошены под одним и тем же углом к горизонту с начальными скоростями 

26. Камень бросили под углом к горизонту со скоростью V0. Его траектория в однородном поле тяжести изображена на рисунке. Сопротивления воздуха нет. Модуль тангенциального ускорения а? на участке А-В-С … (ответ обосновать).
27. Камень бросили под углом к горизонту со скоростью V0. Его траектория в однородном поле тяжести изображена на рисунке. Сопротивления воздуха нет. Модуль нормального ускорения аn на участке А-В-С … (ответ обосновать).
28. Тело брошено под углом 

1. 



29. Тело брошено под углом 

1. 



30. Камень брошен со скоростью ?0 = 15 м/с под углом ? = 30є к горизонту. Радиус кривизны R в верхней точке траектории равен … м. (g = 9,8 м/с 2 )
1. 0,59 2. 1,53 3.5,74 4.17,22 5. 22,96
31. Скорость камня в точке его падения составила с горизонтом угол ?. Нормальное ускорение камня в момент падения равно …
1. gcos? 2. gsin? 3. gtg? 4. gctg? 5. g
32. Материальная точка движется замедленно по криволинейной траектории. Направление скорости показано на рисунке. Направление вектора полного ускорения правильно изображено на рис. …
1. А 2. Б 3. В 4. Г 5. Д
33. Материальная точка движется ускоренно по криволинейной траектории. Направление скорости показано на рисунке. Направление вектора полного ускорения правильно изображено на рис. …
1. А 2. Б 3. В 4. Г 5. Д
34. Материальная точка М движется по окружности со скоростью 

35. Точка М движется по спирали с постоянной по величине скоростью в направлении, указанном стрелками. При этом величина полного ускорения … (ответ обосновать).
36. Тело движется с постоянным нормальным ускорением по траектории, изображенной на рисунке. Для величины скорости тела в точке А ?А и величины скорости тела в точке В ?В справедливо соотношение …

графику. Такому движению может соответствовать
зависимость скорости от времени …
38. Небольшое тело, подвешенное на невесомой и нерастяжимой нити, совершает колебания. Ускорение тела …
1. равно нулю в положении равновесия (нижней точке)
2. равно нулю в крайних точках
3. равно нулю в положении равновесия и в крайних точках
4. ни в одной точке не равно нулю
5. зависит от массы тела
39. Точка движется по окружности радиуса 
1. 0,5 2. 1,0 3. 1,5 4. 2,0 5. 2,5
40. Точка движется по окружности с радиусом R = 2 м согласно уравнению l = Аt 3 , А =2 м/с 3 , l – длина дуги от начала движения. Нормальное ускорение равно тангенциальному в момент времени…с.
1. 2 2. 0,874 3. 0,760 4. 0,667 5. 0,3
41. Материальная точка движется по окружности с постоянной по величине скоростью. Линейную скорость точки увеличили в 2 раза и период обращения увеличили в 2 раза. При этом центростремительное ускорение точки …
1. увеличилось в 4 раза 2. увеличилось в 2 раза 3. не изменилось
4. уменьшилось в 2 раза 5. уменьшилось в 4 раза
42. Две материальные точки начинают двигаться по окружности из одной начальной точки: первая с ускорением 0,1 рад/с 2 , вторая – с ускорением 0,15 рад/с 2 . Впервые после начала движения они встретятся через … с.
1.10,2 2. 31,7 3. 47,5 4. 15,8 5. 75
43. Диск вращается вокруг своей оси, изменяя проекцию своей угловой скорости ?Z (t) так, как показано на рисунке. Вектор углового ускорения 
44. Тело вращается вокруг неподвижной оси по закону 
1. 3,20 2. 1,65 3. 1,60 4. 0,40 5. 0
45. Точка вращается по окружности радиуса R согласно уравнению ?=Аt 3 +Bt 2 +Ct, где А = 7 рад/с 3 , В = 8 рад/c 2 , С = 4 рад/с. Нормальное ускорение точки 
1. 

4. 

46. Точка вращается по окружности радиуса R согласно уравнению ?=Аt 3 +Bt 2 +Ct, где А = 7 рад/с 3 , В = 8 рад/c 2 , С = 4 рад/с. Касательное ускорение точки определяется выражением
1. 



47. Колесо радиусом R = 20 см вращается с угловым ускорением ? = 3,14 рад/с 2 . К концу первой секунды от начала движения тангенциальное ускорение а точек обода колеса равно… м/с.
1. 0,628 2. 1,972 3. 2,070 4. 2,600 5. 3,140
48. На вал радиуса 10 см намотана нить, к концу которой привязана гиря. Опускаясь равноускоренно, гиря прошла расстояние 5 см за 2 с. Тангенциальное ускорение точки, лежащей на поверхности вала равно … см/с 2 .
1. 0,5 2. 5 3. 2,5 4. 3,5 5. 25
49. Частица из состояния покоя начала двигаться по дуге окружности радиуса R = 1 м с постоянным угловым ускорением ? = 2 с -2 . Отношение нормального ускорения к тангенциальному через одну секунду равно …
1. 1 2. 2 3. 3 4. 4 5. 8
50. Шкив радиуса R вращается под действием груза, подвешенного на нитке. Ускорение груза 
1. 




51. Материальная точка движется равнозамедленно по окружности, лежащей в горизонтальной плоскости, по часовой стрелке. Вектор угловой скорости направлен …
1. по касательной к траектории
2. по радиусу к центру окружности
3. по радиусу от центра
5. вверх по оси вращения
52. Материальная точка движется равнозамедленно по окружности, лежащей в вертикальной плоскости, по часовой стрелке. Вектор угловой скорости направлен …
1. по касательной к траектории
2. по радиусу к центру окружности
3. по радиусу от центра
5. к нам
53. Диск, расположенный в горизонтальной плоскости, вращается равнозамедленно по часовой стрелке. Вектор углового ускорения направлен …
1. по касательной к траектории
2. по радиусу к центру окружности
3. по радиусу от центра
4. вниз по оси вращения
5. вверх по оси вращения
54. Материальная точка движется равнозамедленно по горизонтальной окружности против направления часовой стрелки. Вектор углового ускорения направлен по …
1. касательной к окружности
2. радиусу окружности от оси вращения
3. оси вращения вниз
4. оси вращения вверх
5. направлению вектора угловой скорости
55. Закон изменения угла поворота ? со временем имеет вид 

1. 19; 56 2. 56; 46 3. 88; 56 4. 86; 19 5. 76; 29
56. Кинематический закон вращательного движения тела задан уравнением ? = c t 3 , где c = 1 рад/с 3 . Угловая скорость тела в конце третьей секунды равна … рад/с.
1. 3 2. 6 3. 4 4. 9 5. 27
57. Частица движется вдоль окружности радиусом 1 м в соответствии с уравнением 
1. 1 2. 2 3. 3 4. 4 5. 2,5
58. Материальная точка вращается в горизонтальной плоскости относительно неподвижной оси с угловым ускорением ? = Аt 2 , где А=2 рад/с 4 . При t = 0 ?0 = 0. Закон изменения угловой скорости имеет вид …
1. ? = 2t 3 2. ? = 2/3 t 3 3. ? = 4t 4. ? = 4t 3 5. ? = 3/2 t 3
59. Закон изменения угловой скорости материальной точки имеет вид ?=A+Bt, где А=10 рад/с, В=6 рад/с 2 . Угол поворота ? в момент времени t = 5 с равен … рад.
1. 6 2. 40 3. 65 4. 80 5. 125
60. Маховик вращается равнозамедленно с угловым ускорением ? = 2 рад/с 2 . Угол поворота ? при изменении частоты вращения от n 1 = 240 мин -1 до n 2 = 90 мин -1 равен … рад.
1. 1479 2. 136 3. 22 4. 5 5. 4
61. Шарик движется по окружности по закону 
1. 49 2. 63 3. 99 4. 198 5. 396
Динамика материальной точки. Законы сохранение импульса и энергии. Работа. Мощность
1. Масса тела это …
1. количество вещества в теле
2. мера инертности тела
3. отношение веса тела к ускорению свободного падения
4. мера гравитационного взаимодействия тел
5. мера потенциальной энергии тела
2. Законы Ньютона применимы для описания движения тел …
1. в инерциальных и неинерциальных системах отсчета
2. только в инерциальных системах отсчета0
3. только при движении со скоростями, много меньшими скорости света в любых системах отсчета
4. в инерциальных системах отсчета при движении тел с любыми скоростями
5. в инерциальных системах отсчета при движении со скоростями, много меньшими скорости света
3. Известен характер движения тела в некоторой инерциальной системе отсчета. Инерциальной является любая другая система отсчета, в которой у тела …
1. такое же ускорение 0 2. такая же скорость 3. такая же координата
4. такая же траектория 5. такое же перемещение
4. Тело массой m движется под действием постоянной по модулю и направлению силы 
1. а 2. б 3. в 4. г 5. д
5. Материальная точка М движется по окружности со скоростью ?. На рис. 1 показан график зависимости скорости 



6. Скорость автомобиля изменялась со временем, как показано на графике зависимости ?(t). В момент времени t1 автомобиль поднимался по участку дуги. Направление результирующей всех сил, действующих на автомобиль в этот момент времени, правильно отображает вектор …


1. не изменяется со временем и действует по направлению движения
2. не изменяется со временем и действует против направления движения
3. не изменяется со временем по величине и направлению
5. изменяется со временем по величине
8. К телу, находящемуся в состоянии покоя на гладком горизонтальном столе, приложена постоянная горизонтально направленная сила. Во время действия этой силы не будет изменяться …
1. положение тела 2. ускорение тела 3. скорость тела
4. импульс тела 5. кинетическая энергия тела
9. Тело массой m=1 кг движется по плоскости таким образом, что зависимость проекций скорости тела от времени имеет вид 

1. 1 2. 3 3. 4 4. 5 5. 7
10. Тело, массой 2 кг движется прямолинейно по закону 
1. 3,2 2. 2,4 3. 1,6 4. 3,6 5. 2,8
11. Молекула массой m , летящая со скоростью ?, ударяется о стенку сосуда под углом ? к нормали и упруго отскакивает от неё без потери скорости. Импульс силы, полученный стенкой во время удара, равен …
1. 




12. Упругий шар массой 1 кг ударяется о стенку со скоростью 20 м/с под углом 60є к нормали и отскакивает от него под тем же углом, причем численное значение скорости не изменяется. Импульс силы, действовавшей на стенку, равен … Н·с.
1. 34,8 2. 20 3. 17,4 4. 0 5. 40
13. Тело движется вдоль оси х согласно уравнению 
1. возрастает 2. убывает 3. не изменяется
4. сначала возрастает, затем убывает 5. равен нулю
14. Человек входит в лифт, который затем начинает двигаться равномерно вверх, при этом вес человека…
- увеличится
- будет зависеть от скорости движения лифта
- уменьшится
- не изменится
- станет равным нулю
🎬 Видео
Материальная точка. Система отсчета | Физика 9 класс #1 | ИнфоурокСкачать

Урок 47. Неравномерное движение по окружности. Тангенциальное ускорениеСкачать

Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Равномерное движение точки по окружности | Физика 10 класс #7 | ИнфоурокСкачать

Вращательное движение. 10 класс.Скачать

КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ - Угловое Перемещение, Угловая Скорость, Центростремительное УскорениеСкачать

Физика 9 класс. Движение по окружностиСкачать

Физика | Равномерное движение по окружностиСкачать

Криволинейное, равномерное движение материальной точки по окружности. Практическая часть. 9 класс.Скачать

Урок 7. Механическое движение. Основные определения кинематики.Скачать

ФИЗИКА 10 класс : Механическое движение | Материальная точка, траектория, перемещение.Скачать

Урок 94. Вычисление моментов инерции телСкачать