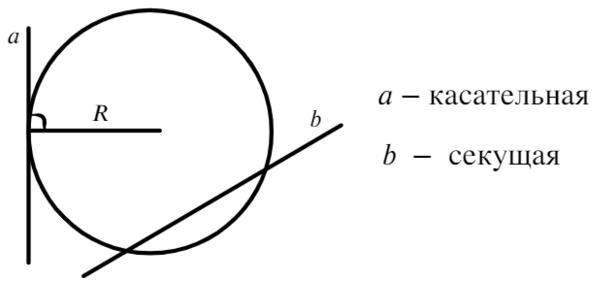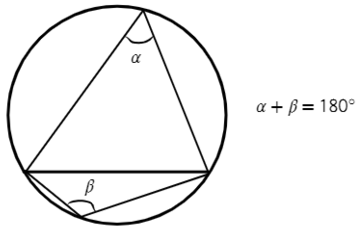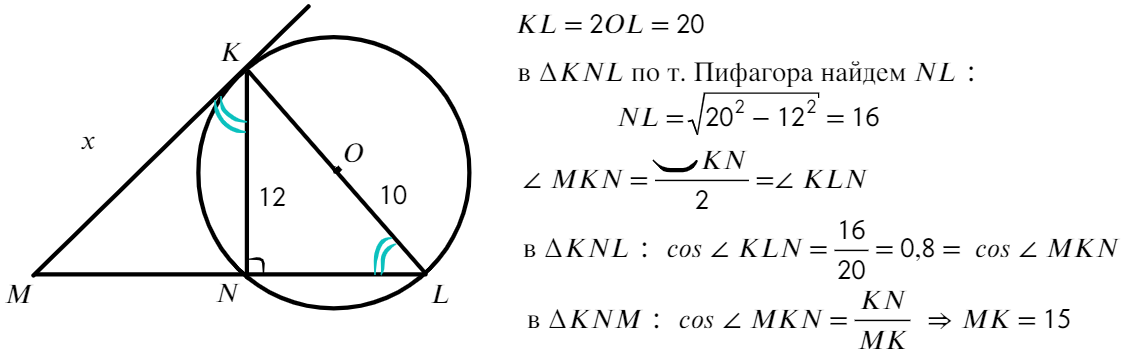Открытый банк заданий по теме окружность. Задания B6 из ЕГЭ по математике (профильный уровень)
- Задание №1070
- Условие
- Решение
- Ответ
- Задание №1069
- Условие
- Решение
- Ответ
- Задание №1068
- Условие
- Решение
- Ответ
- Задание №896
- Условие
- Решение
- Ответ
- Задание №51
- Условие
- Решение
- Ответ
- Задание №48
- Условие
- Решение
- Ответ
- Задание №47
- Условие
- Решение
- Ответ
- Задание №46
- Условие
- Решение
- Теория и практика окружности
- Аналогично в каждом отрезке присутствует точка, вне окружности (О).
- Задача №1. Дано на рисунке:
- Достаточно вспомнить свойства центральных и вписанных углов.
- Ответ: 39°
- Задача №2. Дано на рисунке:
- Найти нужно меньшую дугу BD
- Ответ: 100°
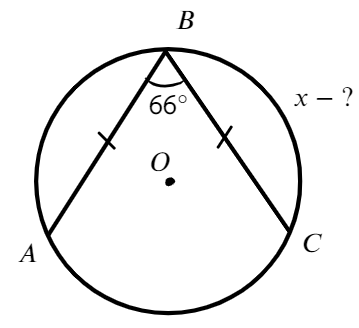
- Найти меньшую дугу ВС
- Ответ: 114°
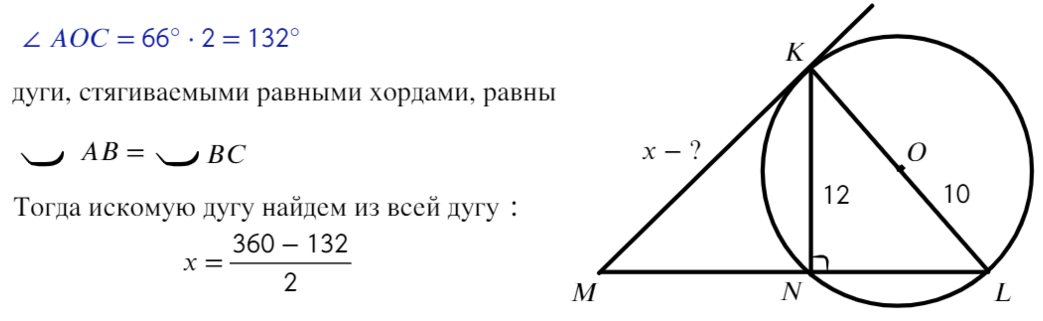
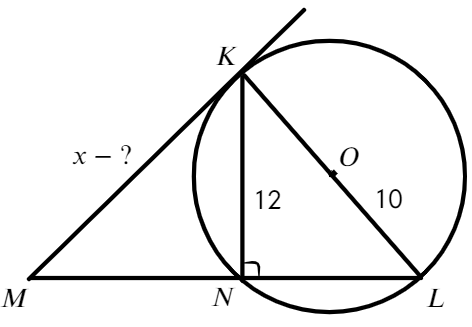
- Задача №4. Дано на рисунке:
- Найти отрезок МК
- Ответ: МК = 15.
- Задача №5. Дано на рисунке:
- Попробуй найти подобные треугольники
- Ответ: 6
- Задача №5. Дано на рисунке:
- Без свойства секущей и касательной здесь будет тяжело
- Ответ: 12√7.
- Я могу долго тебе показывать, как решать задачи, но без твоих усилий ничего не выйдет.
- О треугольниках О четырехуголниках
- Задачи ЕГЭ на движение по окружности
- 💥 Видео
Видео:Разбор задания №21 из ЕГЭ по базовой математике | Базовая математика ЕГЭ 2022 | УмскулСкачать

Задание №1070
Условие
Через концы A и B дуги окружности с центром O проведены касательные AC и BC . Меньшая дуга AB равна 56^. Найдите угол ACB . Ответ дайте в градусах.
Решение
Центральный угол равен угловой величине дуги, на которую он опирается, то есть
angle BOA = 56^. Углы OBC и OAC прямые как углы между касательными и радиусами, проведёнными в точки касания. Сумма углов четырёхугольника равна 360^, можем найти угол ACB .
Ответ
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Задание №1069
Условие
Точки A , B , C , расположенные на окружности, делят её на три дуги, градусные меры которых относятся как 2:3:4 . Найдите больший угол треугольника ABC . Ответ дайте в градусах.
Решение
Угловая величина всей окружности составляет 360^, дуги, на которые опираются углы треугольника, составляют 2 , 3 и 4 из 2 + 3 + 4 = 9 частей, то есть большая из них равна frac49 окружности, 360^cdotfrac49=160^. Вписанный угол равен половине дуги, на которую он опирается, то есть 160^ : 2 = 80^.
Ответ
Видео:Задача с конусом по стереометрии | Базовая математика ЕГЭ 2023 | УмскулСкачать

Задание №1068
Условие
Хорда AB делит окружность на две дуги, градусные меры которых относятся как 13 : 7 . Под каким углом видна эта хорда из точки C , принадлежащей большей дуге окружности? Ответ дайте в градусах.
Решение
Угловая величина всей окружности составляет 360^, дуга, на которую опирается угол C , составляет 7 из 7+13 = 20 частей, то есть frac окружности, 360^cdot frac = 126^. Вписанный угол равен половине дуги, на которую он опирается, то есть 126^ : 2 = 63^.
Ответ
Видео:ОКРУЖНОСТЬ / Разбор задания из ЕГЭ база #27874Скачать

Задание №896
Условие
Найдите вписанный угол, опирающийся на дугу, длина которой равна frac13 длины окружности. Ответ дайте в градусах.
Решение
Угловая величина всей окружности составляет 360^, дуга составляет треть окружности, то есть 360^:3=120^. Вписанный угол равен половине дуги, на которую он опирается, то есть 120^:2=60^.
Ответ
Видео:ВСЕ ПРОТОТИПЫ 20-ОЙ ЗАДАЧИ | Базовая математика 2023Скачать

Задание №51
Условие
На рисунке изображена окружность с центром O . Прямые AC и BD являются диаметрами окружности. Угол ACB равен 21^ . Найдите угол AOD . Ответ дайте в градусах.
Решение
Так как угол ACB вписан в окружность, то градусная мера дуги AB , на которую он опирается, в 2 раза больше величине этого угла, и равна:
cup AB=2cdotangle ACB=2cdot21^=42^
Так как BD — диаметр окружности, то его градусная мера равна 180^ . Найдем градусную меру угла дуги AD :
Так как угол AOD — центральный, то его величина равна градусной мере дуги окружности AD , следовательно:
angle AOD=cup AD=138^
Ответ
Видео:ТОП-3 конструкции с окружностями для №16 из ЕГЭ 2023 по математикеСкачать

Задание №48
Условие
Угол ACB равен 54^ . Градусная мера дуги AB окружности, не содержащих точек D и E , равна 138^ . Найдите угол DAE . Ответ дайте в градусах.
Решение
Угол DAE мы можем найти зная два остальных угла треугольника ACD . Угол ACB нам известен и равен углу ACD . Угол ADC является разностью развернутого угла BDC и угла ADB . Угол ADB является вписанным в окружность, а значит его величина равна половине градусной меры дуги, на которую он опирается.
Из условия задачи градусная мера дуги AB известна. Найдем угол ADB :
Найдем угол ADC :
Угол DAE равен углу DAC . Зная два угла треугольника, найдем искомый угол DAE :
Ответ
Видео:Планиметрия с окружностями | Задачи из ЕГЭ прошлых лет | №17 ЕГЭ по математикеСкачать

Задание №47
Условие
На рисунке изображена окружность с центром O . Прямые CA и CB являются касательными к окружности. Меньшая дуга AB равна 64^ . Найдите угол ACB . Ответ дайте в градусах.
Решение
Прямые CA и CB являются касательными к окружности, значит они образуют прямой угол с радиусом окружности, то есть с прямыми OA и OB . Сумма углов четырехугольника равна 360^ . Найдем неизвестный угол ACB :
Ответ
Видео:Щелчок по математике I №9 Текстовые задачи всех видовСкачать

Задание №46
Условие
На рисунке изображена окружность с центром O . Угол ACO равен 27^ . Сторона CA – касательная к окружности. Сторона CO пересекает окружность в точке B. Найдите величину меньшей дуги окружности AB . Ответ дайте в градусах.
Решение
Прямая AC является касательной к окружности, значит радиус AO образует с ней прямой угол, следовательно треугольник AOC прямоугольный. Величину меньшей дуги окружности AB вы можем найти зная градусную меру угла AOB . Учитывая, что сумма углов треугольника равна 180^ , найдем угол AOB :
Так как угол AOB – центральный, то величина меньшей дуги окружности AB равна градусной мере этого угла, а значит величина дуги равна 63^
Видео:ЕГЭ ПО МАТЕМАТИКЕ | ДВИЖЕНИЕ ПО ОКРУЖНОСТИ | +1 БАЛЛ ЗА 5 МИНУТ |Скачать
Теория и практика окружности
Свойства касательных и секущих.
Площадь, сектор, длина окружности.
Задачи на окружности.
По статистике окружности никто не любит, но при этом леденец любим, солнце любим, давай и окружность полюбим!
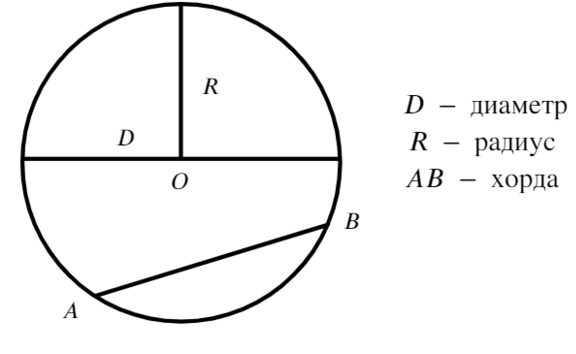
Окружность − геометрическое место точек плоскости, равноудаленных от одной ее точки (центра). На рисунке центр − точка О.
В окружности может быть проведено 3 типа отрезка:
Отрезок, проходящий через две точки окружности, но не через центр, называют хордой (AB).
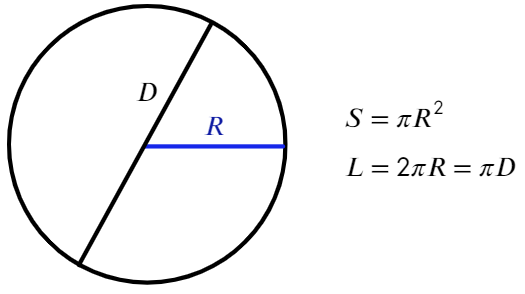
Хорда, проходящая через центр окружности, называется диаметром (самая большая хорда в окружности − диаметр (D)).
Радиус − отрезок, соединяющий центр окружности с точкой на окружности. Диаметр в два раза больше радиуса (R).
А также две прямые снаружи от окружности:
Касательная имеет одну общую точку с окружностью. Сразу стоит сказать о том, что радиус, проведенный в точку касания, будет иметь с касательной угол 90°.
Секущая пересекает окружность в двух точках, внутри окружности получается хорда или, в частном случае, диаметр.
Теперь чуть-чуть об углах и дугах:
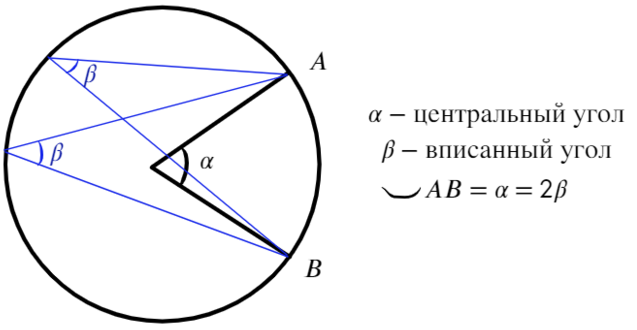
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают ее. Он в два раза меньше дуги, на которую опирается.
Центральный угол — это угол, вершина которого находится в центре окружности, равен дуге на которую опирается.
Вписанные углы, опирающиеся на одну дугу, равны между собой (β=β=α/2) и равны половине дуги, на которую опираются.
Градусная мера дуги – величина в °, соответствует центральному углу. Длина дуги равна α.
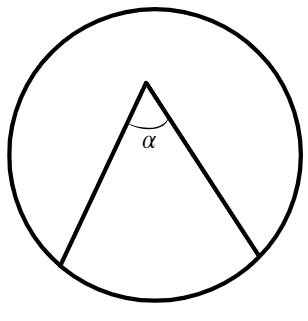
А вот такой угол НЕвписанный, такой угол «никто и звать никак».
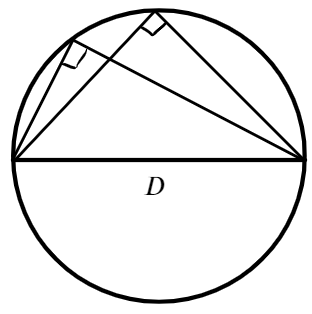
Можно сделать вывод, что вписанный угол, который опирается на половину дуги окружности, будет прямым, а также будет опираться на диаметр:
Любая пара углов, опирающихся на одну и ту же хорду, вершина которых находится по разные стороны от хорды, составляет в сумме 180°.
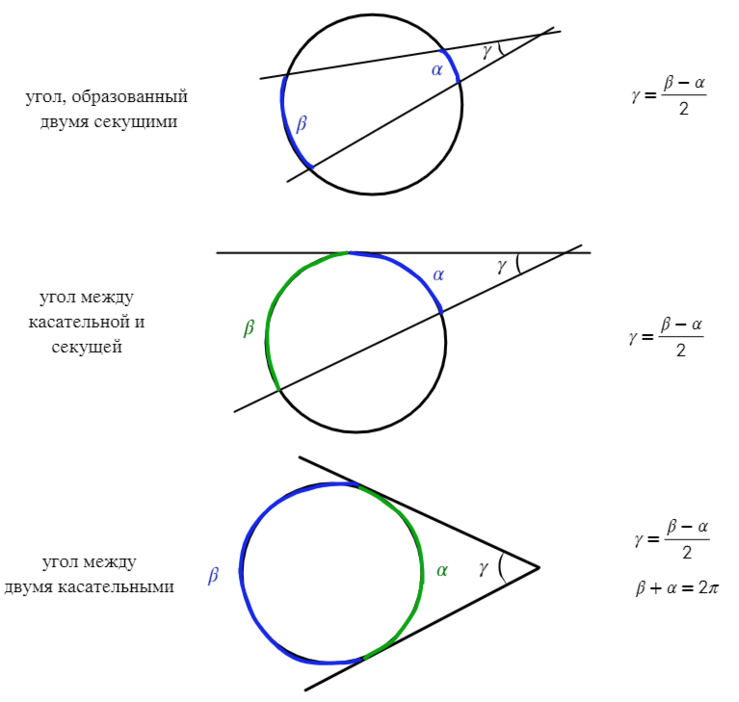
Запишем основные свойства углов в окружности:
Нашел что-то общее?
Если угол находится вне окружности, без разницы, чем он получен (касательной или секущей), то найти его можно через половину разности дуг.
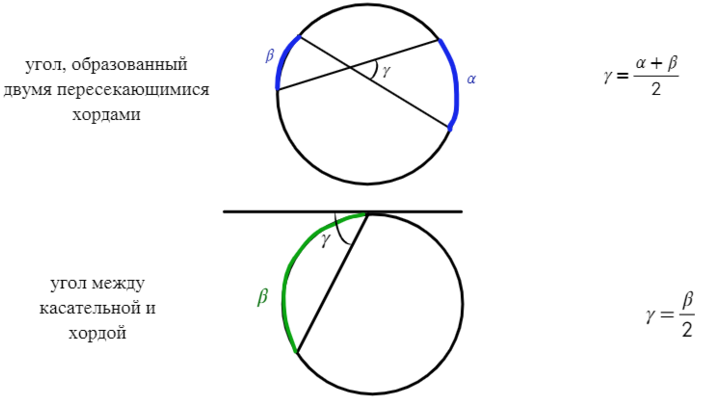
Если угол находится внутри окружности, то находим его через полусумму дуг.
Если есть одна дуга, которая находится на требуемом угле, то угол равен половине этой дуги.
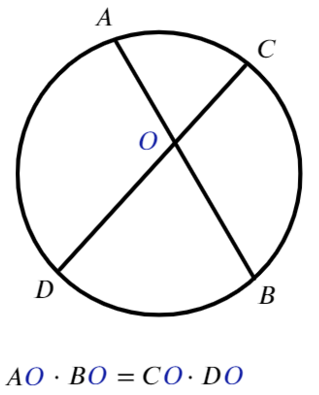
Для любых двух хорд, проходящих через некоторую точку О, выполняет равенство:
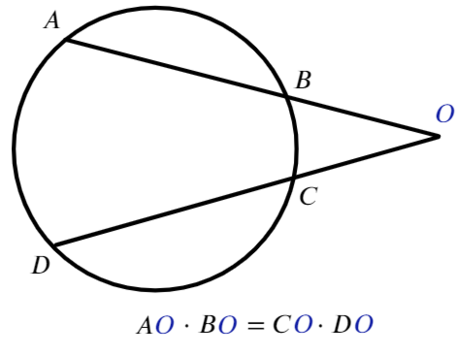
Для любых двух секущих, проходящих через некоторую точку O, выполняется равенство:
Согласен, что они похожи, особенно если не смотреть на картинки.
Как не перепутать такие равенства? В каждом отрезке должна присутствовать точка, вне окружности (О).
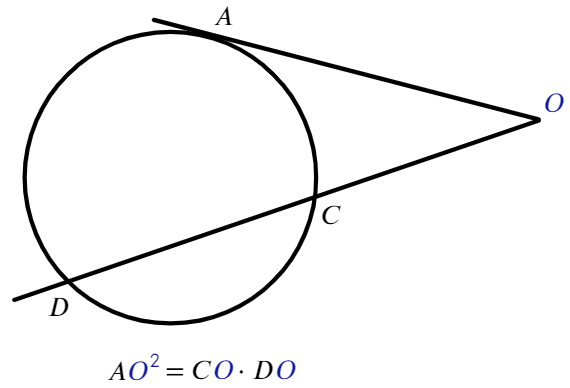
Если из точки, лежащей вне окружности, проведены касательная и секущая:
Аналогично в каждом отрезке присутствует точка, вне окружности (О).
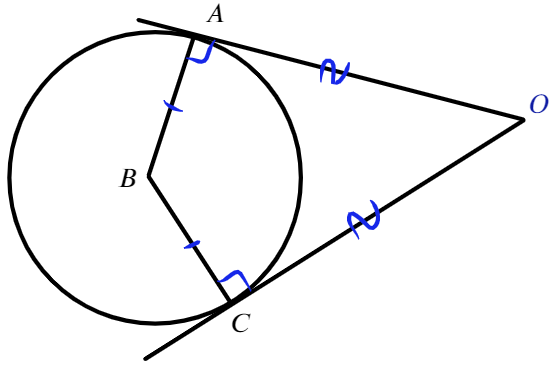
Если теперь провести две касательные из точки O, то получим такие равные отрезки:
Касательные равны, как, сообственно, и радиусы!
Площадь и длина окружности находятся по формуле:
По своему определению число π показывает, во сколько раз длина окружности больше диаметра, отсюда такая формула: L = πD
Если хочешь вывести площадь круга, можешь проинтегрировать длину окружности относительно R или вывести зависимость, как сделал Архимед!
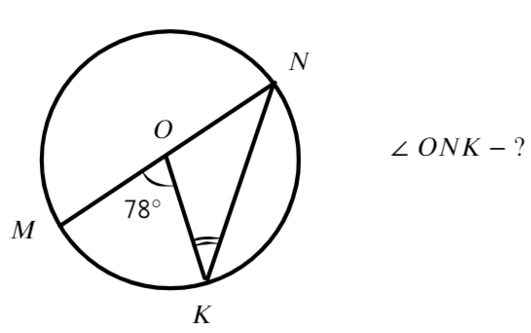
Задача №1. Дано на рисунке:
Достаточно вспомнить свойства центральных и вписанных углов.
Ответ: 39°
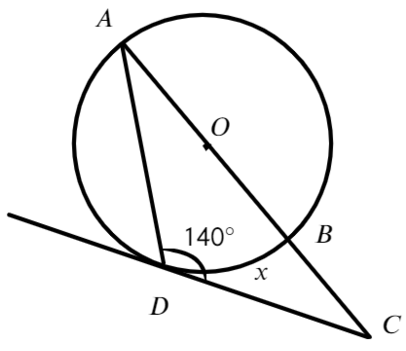
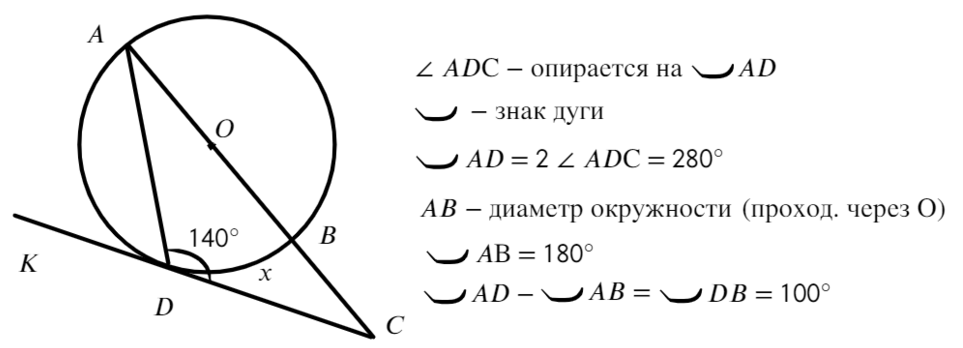
Задача №2. Дано на рисунке:
Найти нужно меньшую дугу BD
Ответ: 100°
Задача №3. Дано на рисунке:
Найти меньшую дугу ВС
Ответ: 114°
Задача №4. Дано на рисунке:
Найти отрезок МК
Ответ: МК = 15.
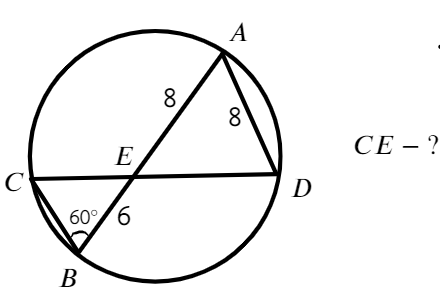
Задача №5. Дано на рисунке:
Попробуй найти подобные треугольники
Ответ: 6
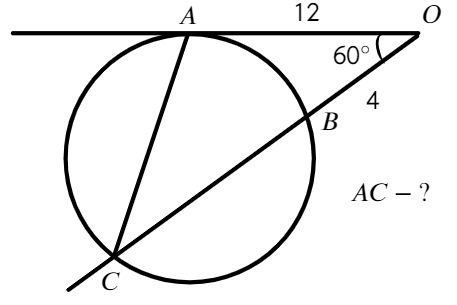
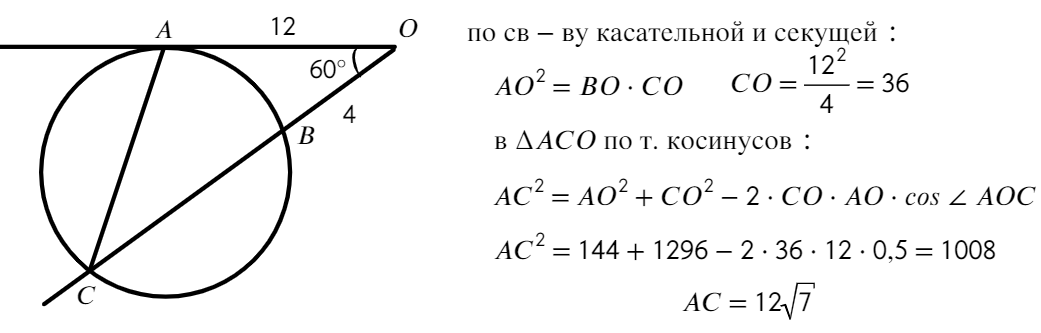
Задача №5. Дано на рисунке:
Без свойства секущей и касательной здесь будет тяжело
Ответ: 12√7.
Я могу долго тебе показывать, как решать задачи, но без твоих усилий ничего не выйдет.
О треугольниках
О четырехуголниках
p.s. Не бойся ошибаться и задавать вопросы!
Если нашел опечатку, или что-то непонятно − напиши.
Видео:движение по кругу | математика ЕГЭ | ВебиумСкачать

Задачи ЕГЭ на движение по окружности
Секрет задач на движение по окружности: тот, кто обгоняет, проезжает на 1 круг больше, если это первый обгон. И на n кругов больше, если обогнал другого в n-ный раз.
Из одной точки круговой трассы, длина которой равна 8 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 114 км/ч, и через 20 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Автомобили стартовали одновременно, и первый автомобиль через 20 минут после старта опережал второй автомобиль на один круг. Значит, за эти 20 минут, то есть за часа он проехал на 1 круг больше – то есть на 8 км больше.
За час первый автомобиль проедет на км больше второго. Скорость второго автомобиля на 24 км/ч меньше, чем у первого, и равна 114 — 24 = 90 км/ч.
Из пункта круговой трассы выехал велосипедист, а через минут следом за ним отправился мотоциклист. Через минут после отправления он догнал велосипедиста в первый раз, а еще через минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна км. Ответ дайте в км/ч.
Во-первых, переведем минуты в часы, поскольку скорость надо найти в км/ч. Скорости участников обозначим за и . В первый раз мотоциклист обогнал велосипедиста через минут, то есть через часа после старта. До этого момента велосипедист был в пути минут, то есть часа.
Запишем эти данные в таблицу:
| велосипедист |
| мотоциклист |
Оба проехали одинаковые расстояния, то есть .
Затем мотоциклист второй раз обогнал велосипедиста. Произошло это через минут, то есть через часа после первого обгона.
Нарисуем вторую таблицу.
| велосипедист |
| мотоциклист |
А какие же расстояния они проехали? Мотоциклист обогнал велосипедиста. Значит, он проехал на один круг больше. Это и есть секрет данной задачи. Один круг — это длина трассы, она равна км. Получим второе уравнение:
Решим получившуюся систему.
Получим, что . В ответ запишем скорость мотоциклиста.
Часы со стрелками показывают часов минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?
Это, пожалуй, самая сложная задача из вариантов ЕГЭ. Конечно, есть простое решение — взять часы со стрелками и убедиться, что в четвертый раз стрелки поравняются через часа, ровно в .
А как быть, если у вас электронные часы и вы не можете решить задачу экспериментально?
За один час минутная стрелка проходит один круг, а часовая часть круга. Пусть их скорости равны (круг в час) и (круга в час). Старт — в . Найдем время, за которое минутная стрелка в первый раз догонит часовую.
Минутная стрелка пройдет на круга больше, поэтому уравнение будет таким:
Решив его, получим, что часа. Итак, в первый раз стрелки поравняются через часа. Пусть во второй раз они поравняются через время . Минутная стрелка пройдет расстояние , а часовая , причем минутная стрелка пройдет на один круг больше. Запишем уравнение:
Решив его, получим, что часа. Итак, через часа стрелки поравняются во второй раз, еще через часа — в третий, и еще через часа — в четвертый.
Значит, если старт был в , то в четвертый раз стрелки поравняются через часа.
Ответ полностью согласуется с «экспериментальным» решением! 🙂
На экзамене по математике вам может также встретиться задача о нахождении средней скорости. Запомним, что средняя скорость не равна среднему арифметическому скоростей. Она находится по специальной формуле:
где — средняя скорость, — общий путь, — общее время.
Если участков пути было два, то
А сейчас покажем вам один из секретов решения текстовых задач. Что делать, если у вас получился в уравнении пятизначный дискриминант? Да, это реальная ситуация! Это может встретиться в варианте ЕГЭ.
Два гонщика участвуют в гонках. Им предстоит проехать 60 кругов по кольцевой трассе протяжённостью 3 км. Оба гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 10 минут. Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 15 минут? Ответ дайте в км/ч.
Первый гонщик через 15 минут после старта обогнал второго на 1 круг. Значит, за 15 минут он проехал на 1 круг, то есть на 3 километра больше. За час он проедет на километров больше. Его скорость на 12 км/ч больше, чем скорость второго.
Как всегда, составляем таблицу и уравнение. 10 минут переведем в часы. Это часа.
Честно преобразовав это уравнение к квадратному, получим:
Пятизначный дискриминант, вот повезло! Но есть и другой способ решения, и он намного проще.
Посмотрим еще раз на наше уравнение:
Заметим, что 180 делится на 12. Сделаем замену:
Это уравнение легко привести к квадратному и решить.
Целый положительный корень этого уравнения: Тогда
Мы решили текстовую задачу с помощью замены переменной. Этот прием в математике используется везде: в решении задач, уравнений и неравенств, в задачах с параметрами и интегрировании. Общее правило: можете сделать замену переменной – сделайте.
💥 Видео
Все о вписанных и описанных окружностях с нуля | PARTAСкачать

ВСЯ СТЕРЕОМЕТРИЯ НА БАЗОВЫЙ ЕГЭ-2023 // КОНЦЕНТРАТ // МАТЕМАТИКАСкачать

Задание 21 (часть 1) | ЕГЭ 2024 Математика (база) | Задачи на смекалкуСкачать

🔴 В окружности с центром O отрезки AC и BD ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

Задачи на движение по окружности. ЕГЭ по математике 2020Скачать

Все об окружностях на ЕГЭ | Профильная математика 2023 | УмскулСкачать

Тригонометрическая окружность. Как выучить?Скачать

Задачи на движение по окружности. Задание 8 ЕГЭ. Задание 21 ЕГЭ.Скачать

Задача про две вневписанные окружности | ЕГЭ. Задание 16. Математика | Борис Трушин |Скачать






.png)