Как начертить объемный треугольник черчение

Видео:Треугольная призма. Ортогональные и изометрическая проекции. Урок 10.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Способы построения изометрической проекции плоских фигур, геометрических тел и деталей

Для выполнения изометрической проекции любой детали не­обходимо знать правила построения изометрических проекций плоских и объемных геометрических фигур.

Правила построения изометрических проекций геометриче­ских фигур. Построение любой плоской фигуры следует начи­нать с проведения осей изометрических проекций.

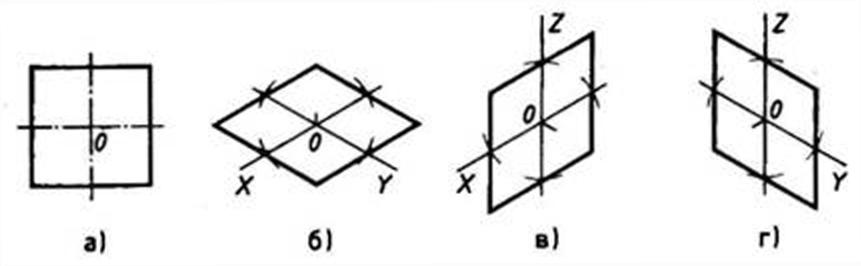
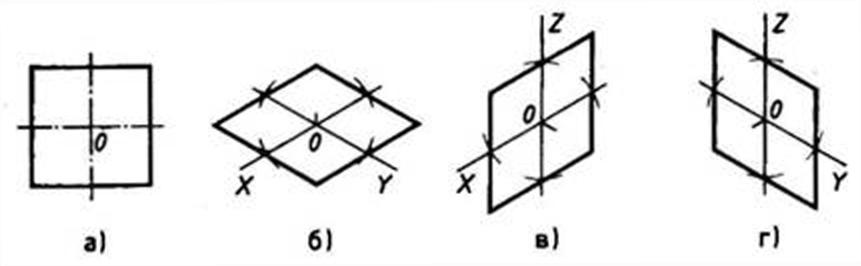
При построении изометрической проекции квадрата (рис. 109) из точки О по аксонометрическим осям откладывают в обе сто­роны половину длины стороны квадрата. Через полученные за­сечки проводят прямые, параллельные осям.

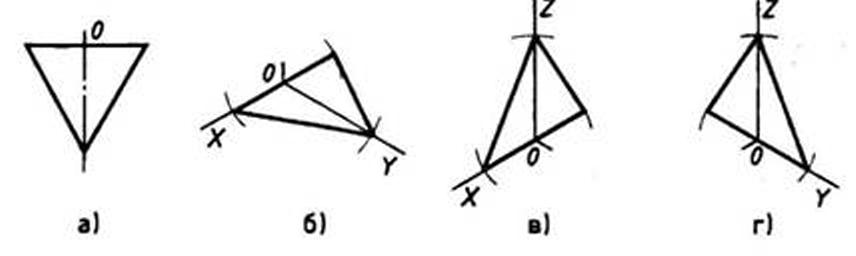
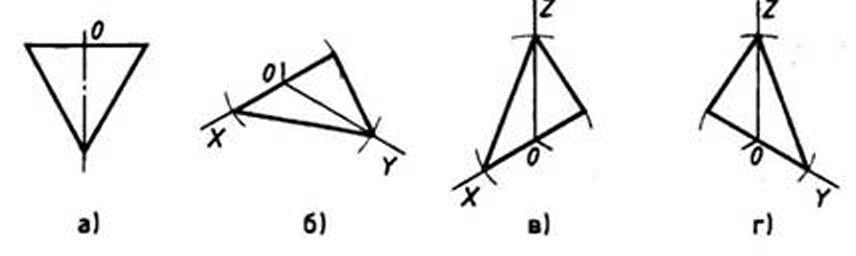
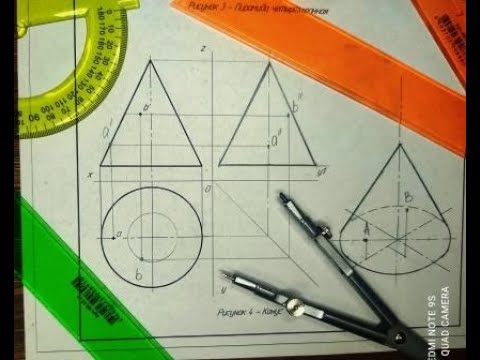
При построении изометрической проекции треугольника (рис. 110) по оси X от точки 0 в обе стороны откладывают отрезки, равные половине стороны треугольника. По оси У от точки О откладывают высоту треугольника. Соединяют полученные за­сечки отрезками прямых.

Рис. 109. Прямоугольная и изометрические проекции квадрата

Рис. 110. Прямоугольная и изометрические проекции треугольника

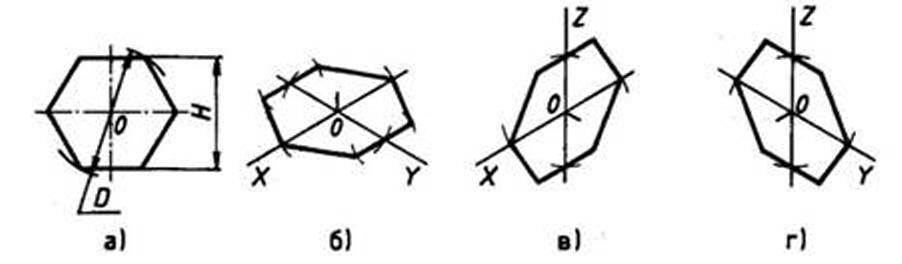
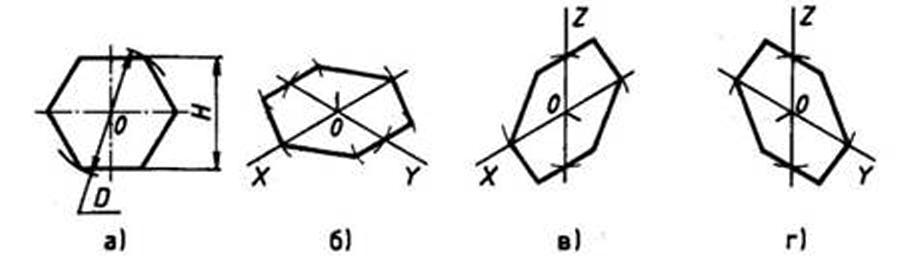
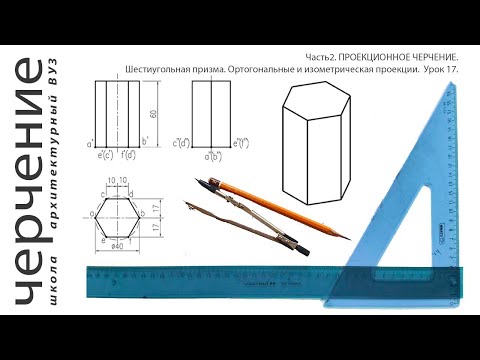
При построении изометрической проекции шестиугольника (рис. 111) из точки О по одной из осей откладывают (в обе сторо­ны) радиус описанной окружности, а по другой — H/2. Через полученные засечки проводят прямые, параллельные одной из осей, и на них откладывают длину стороны шестиугольника. Со­единяют полученные засечки отрезками прямых.

Рис. 111. Прямоугольная и изометрические проекции шестиугольника

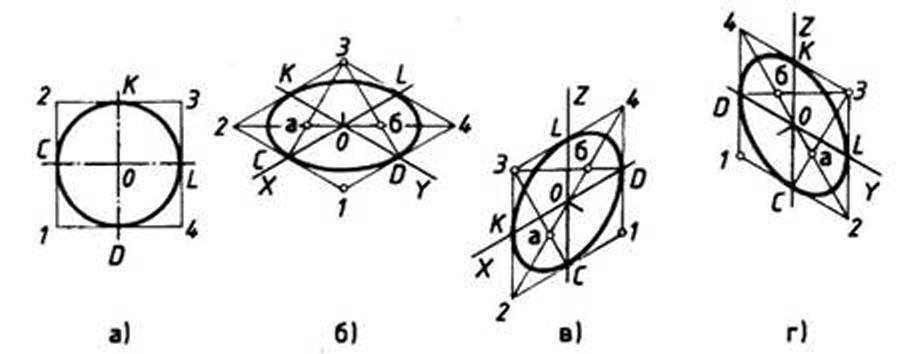
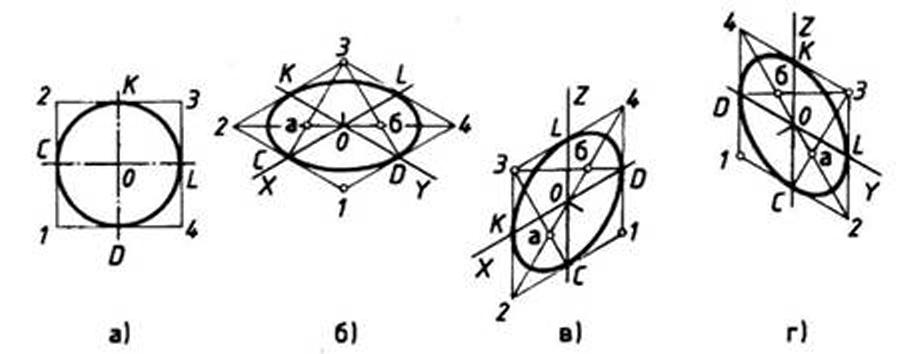
Рис. 112. Прямоугольная и изометрические проекции круга

При построении изометрической проекции круга (рис. 112) из точки О по осям координат откладывают отрезки, равные его радиусу. Через полученные засечки проводят прямые, парал­лельные осям, получая аксонометрическую проекцию квадрата. Из вершин 1, 3 проводят дуги CD и KL радиусом 3С. Соединяют точки 2 с 4, 3 с С и 3 с D. В пересечениях прямых получаются центры а и б малых дуг, проведя которые получают овал, заме­няющий аксонометрическую проекцию круга.

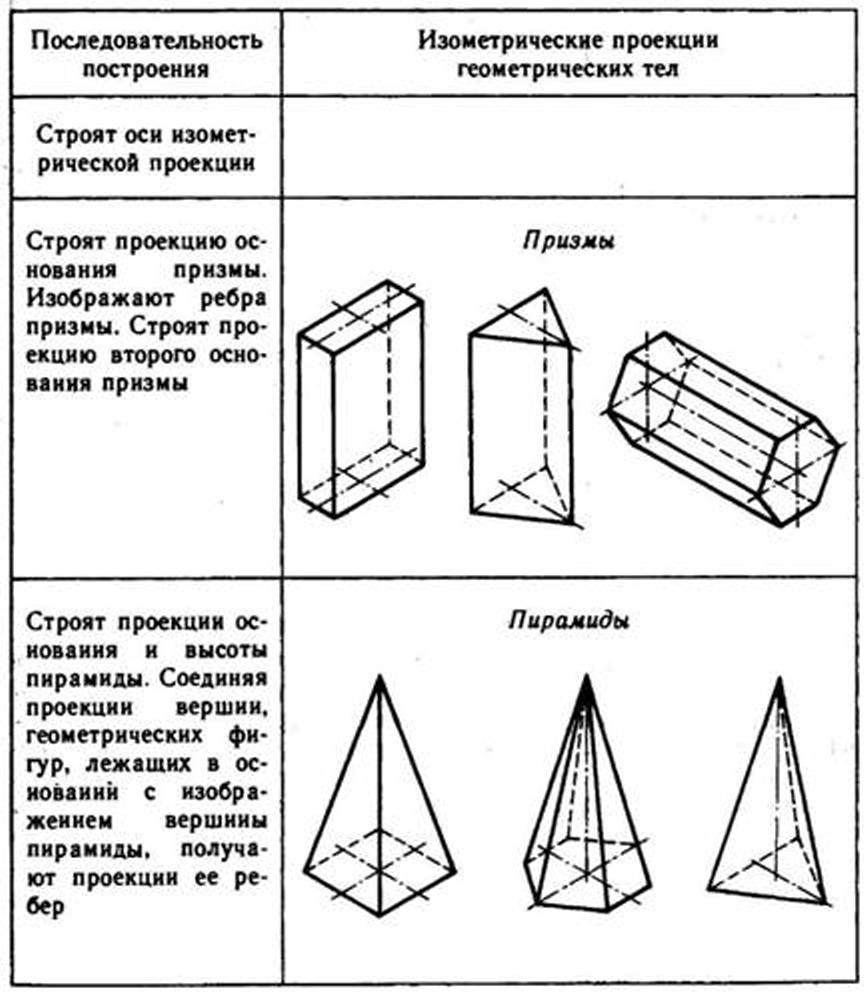
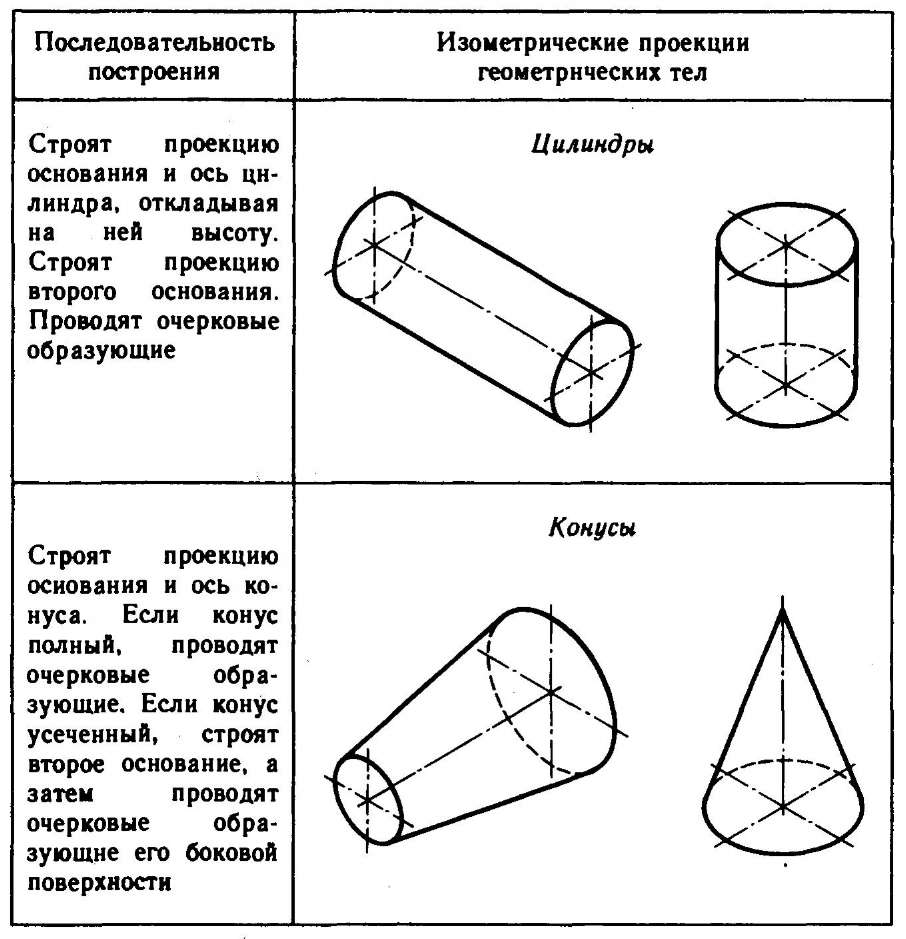
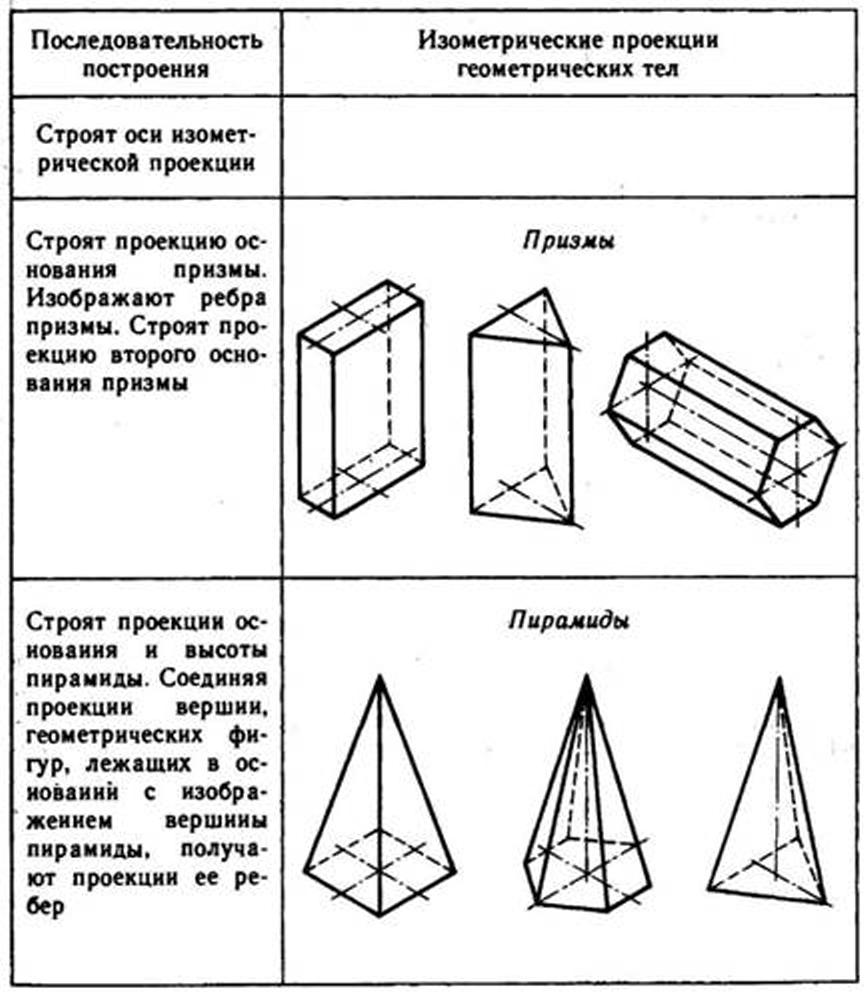
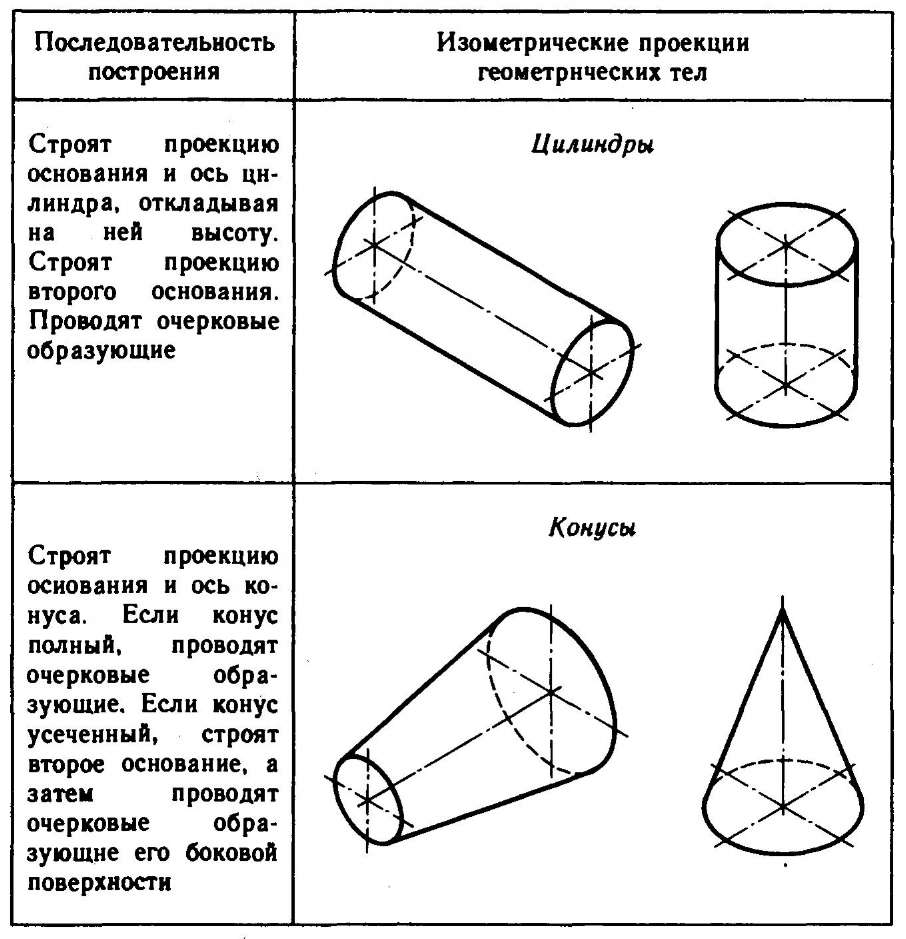
Используя описанные построения, можно выполнить аксоно­метрические проекции простых геометрических тел (табл. 10).

10. Изометрические проекции простых геометрических тел

Способы построения изометрической проекции детали:

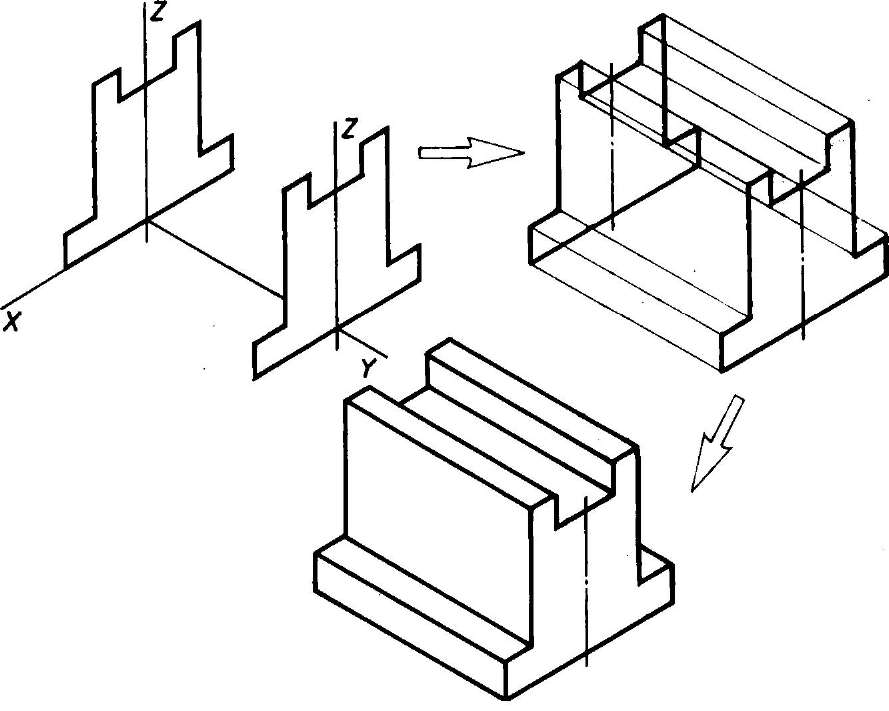
1. Способ построения изометрической проекции детали от формообразующей грани используется для деталей, форма кото­рых имеет плоскую грань, называемую формообразующей; ши­рина (толщина) детали на всем протяжении одинакова, на боко­вых поверхностях отсутствуют пазы, отверстия и другие элемен­ты. Последовательность построения изометрической проекции заключается в следующем:

1) построение осей изометрической проекции;

2) построение изометрической проекции формообразующей грани;

3) построение проекций остальных граней посредством изо­бражения ребер модели;

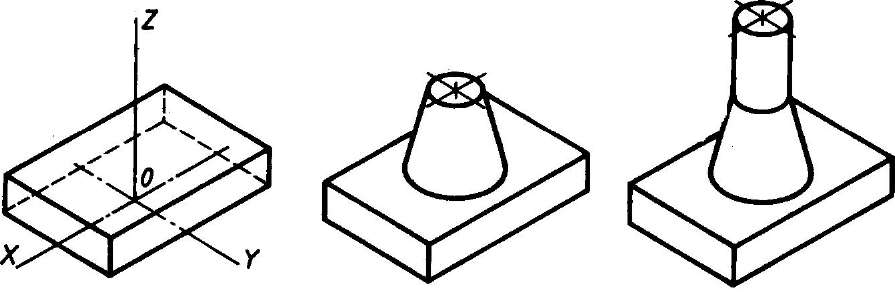
Рис. 113. Построение изометрической проекции детали, начиная от фор­мообразующей грани

4) обводка изометрической проекции (рис. 113).

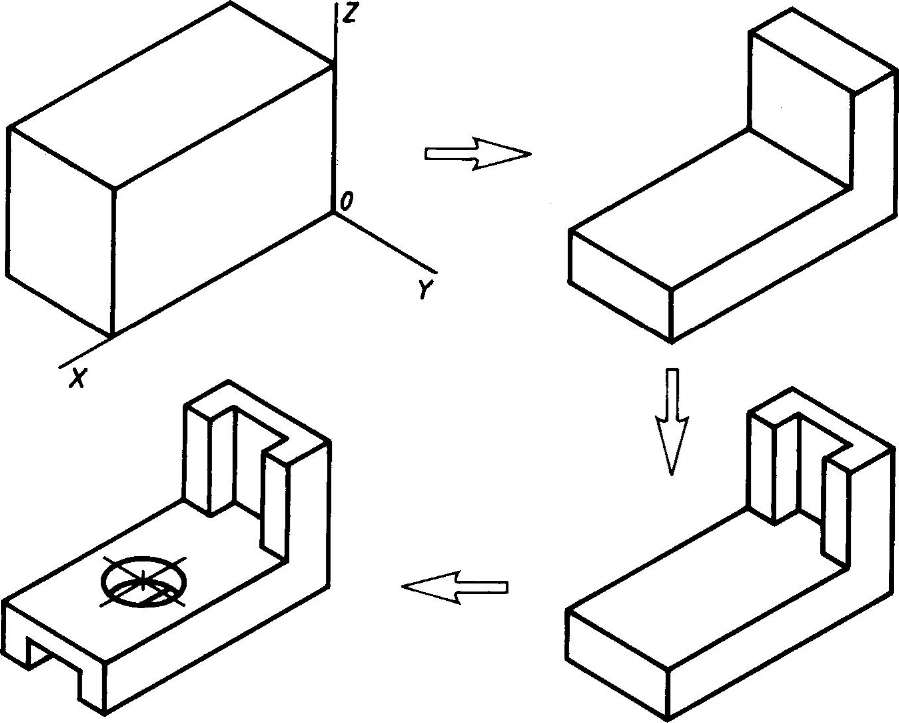
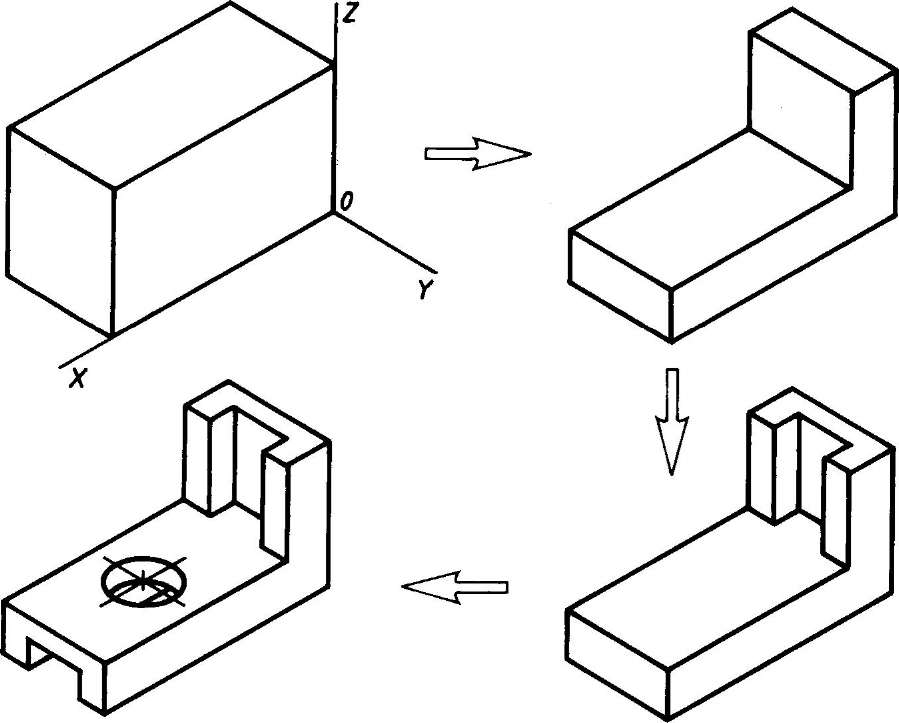
1. Способ построения изометрической проекции на основе по­следовательного удаления объемов используется в тех случаях, когда отображаемая форма получена в результате удаления из исходной формы каких-либо объемов (рис. 114).
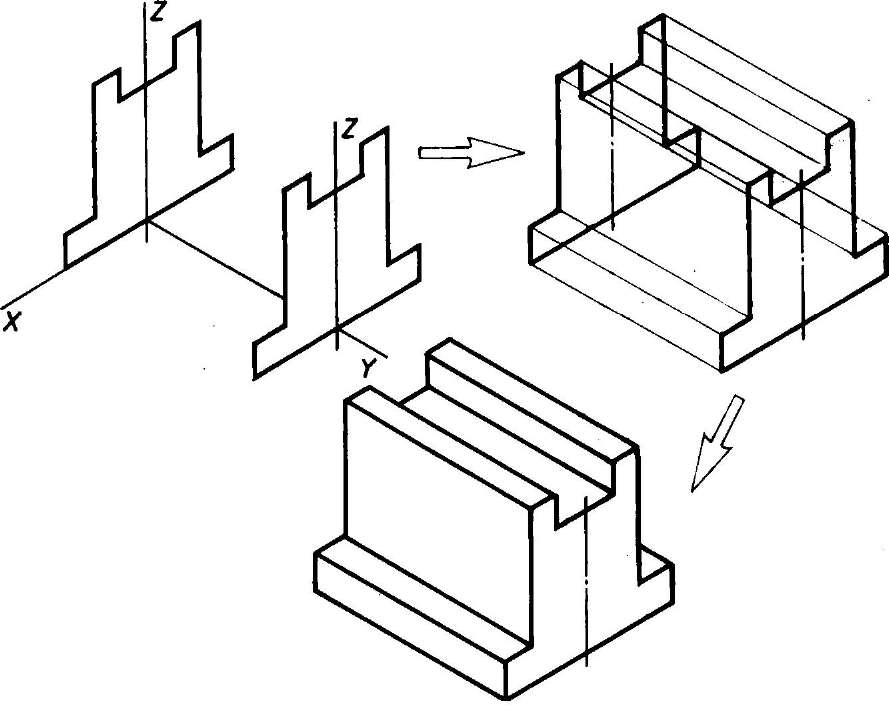
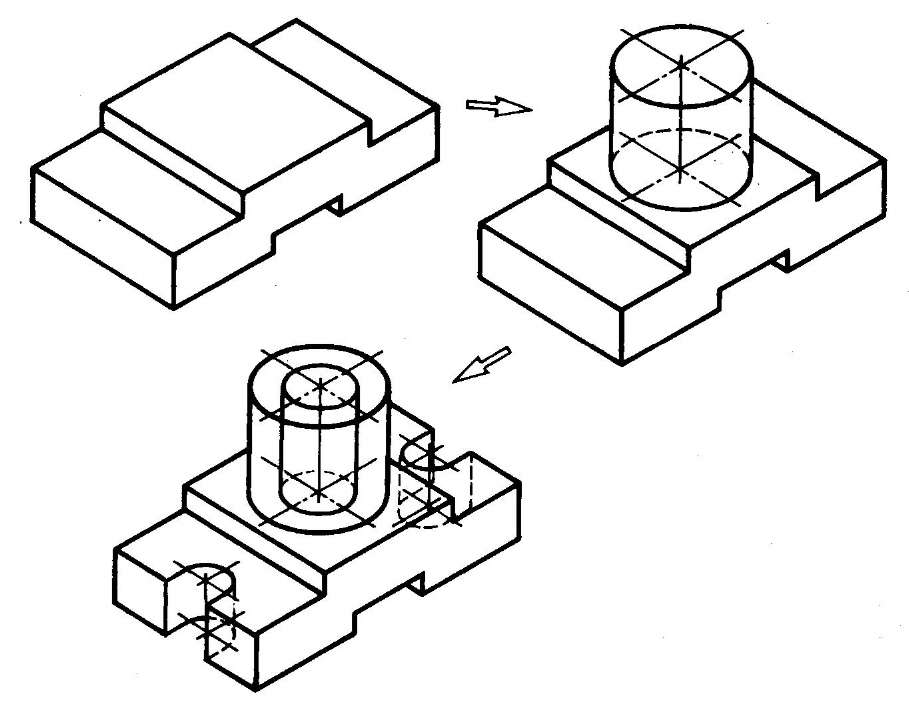
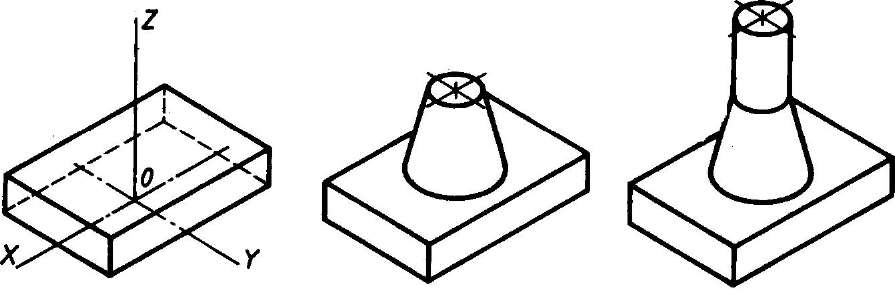
2. Способ построения изометрической проекции на основе по­следовательного приращения (добавления) объемов применяется для выполнения изометрического изображения детали, форма которой получена из нескольких объемов, соединенных опреде­ленным образом друг с другом (рис. 115).
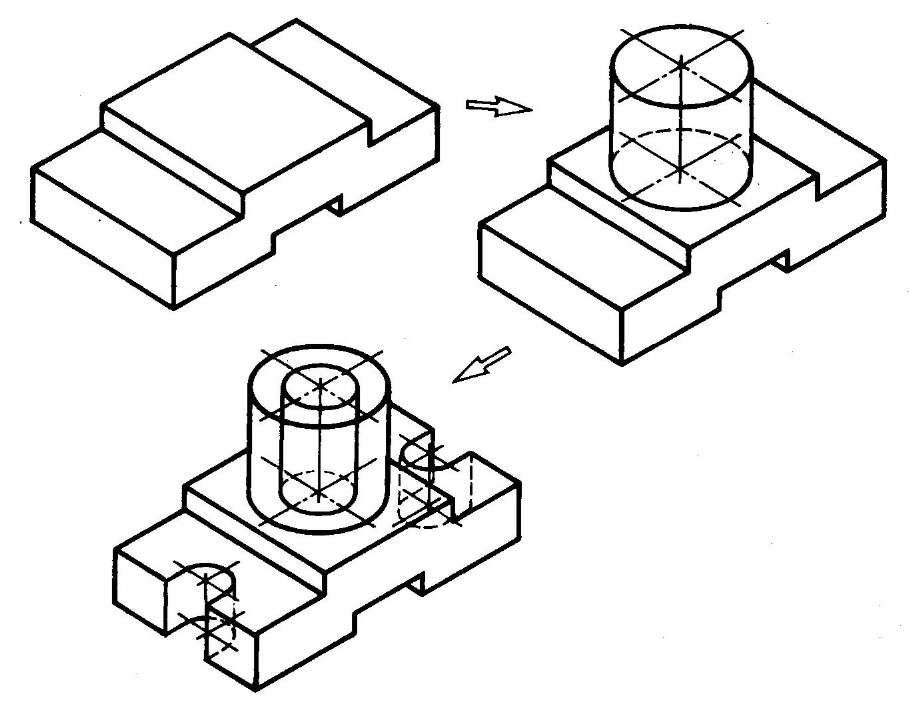
3. Комбинированный способ построения изометрической про­екции. Изометрическую проекцию детали, форма которой полу­чена в результате сочетания различных способов формообразо­вания, выполняют, используя комбинированный способ построе­ния (рис. 116).

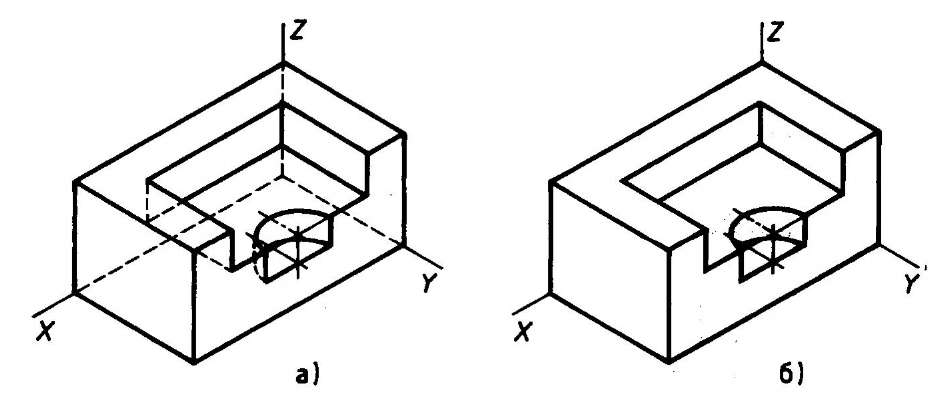
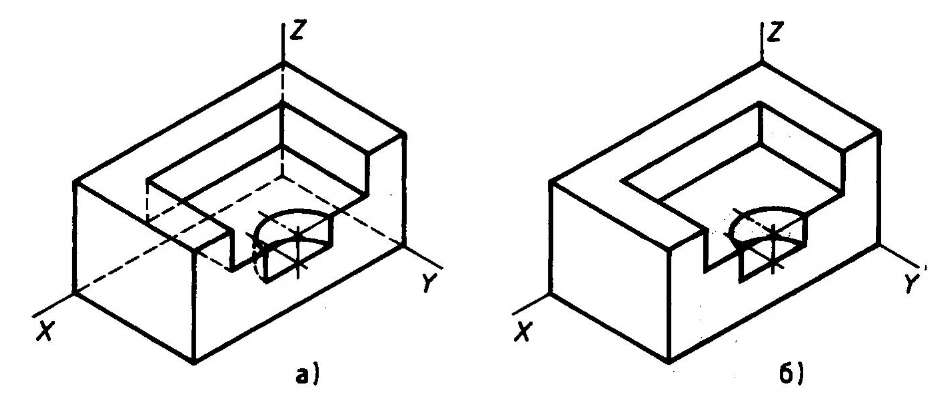
Аксонометрическую проекцию детали можно выполнять с изображением (рис. 117, а) и без изображения (рис. 117, б) неви­димых частей формы.

Рис. 114. Построение изометрической проекции детали на основе последовательного удаления объемов

Рис. 115 Построение изометрической проекции детали на основе последовательного приращения объемов

Рис. 116. Использование комбинированного способа построения изометрической проекции детали

Рис. 117. Варианты изображения изометрических проекций детали: а — с изображением невидимых частей;
б — без изображения невидимых частей

Видео:Как начертить цилиндр в объемеСкачать

Как начертить объемный прямоугольник

Все предметы и фигуры размещены в пространстве. Даже в простом рисунке стоит понимать совсем неразные предметы, а все, что находится на нем, и все, что мы хотим изобразить. Стоит рассматривать это как один поток форм и линий, белого и черного цвета, света и тени.

Рисунок нужно воспринимать как пространство на бумаге, где существует плоскость и пропорции всех находящихся предметов, свет и тень, которая направляется по форме предмета.

Основные геометрические фигуры:

Двухмерные плоские фигуры

Трехмерные фигуры, у которых есть объем

Абсолютно все предметы в основе своего построения имеют эти фигуры.

Куб — фигура, основой которой является трехмерное изображение в пространственном соотношении листа. В кубе есть все геометрические параметры, такие как: вертикальность, горизонтальность и глубина. В самом кубе заложено понятие рисунка в целом.

Для начала понимания рисунка, мы поработаем именно с ним. При помощи образно-логических построений, мы с вами будем развивать мышление за счет аналитики формы. Для большего понимания и анализа рисунка есть несколько упражнений.

Упражнения

Садимся за мольберт, берем большой лист бумаги, можно недорогой, или вообще кусок обоев (в этом упражнении бумага особо значения не имеет). Рисуем квадрат, естественно пытаемся сделать так, чтобы его стороны были ровными, а линии прямыми.

Итак, — мы видим обычный квадрат, совсем неинтересный и не впечатляющий, но это только в данный момент…

Делаем из квадрата куб карандашом: прорисовываем линии от граней примерно с углом 45 градусов. Дорисовываем заднюю часть и… у нас получается кубик. Но снова никакого пространства у нас в листе мы не видим. Свободно можно попутать ближайшие и дальние грани. Сейчас это просто несколько линий на бумаге.

Чтобы нам чувствовать пространство, нужно придать рисунку плавности. То есть сделать так, чтобы нам было ясно, где передняя часть рисунка, а где задняя.

Сторону куба, находящуюся ближе к нам, нужно выделить, сделать четче и передать активнее. Берем свой карандаш и наведем жирным тоном передние грани. Сейчас мы уже можем увидеть, где ближняя сторона, а где сторона находится дальше от нас.

Вот таким способом мы передали пространство, чтобы добиться желаемого результата. Но это далеко не все. Сейчас важно правильно передать плавность, чтобы получить объемность в рисунке.

Представляем вашему вниманию небольшой видеоурок на тему оптических иллюзий.

Видео:Шестиугольная призма.Ортогональные и изометрическая проекции.Урок 17.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Или дневник начинающего художника

Продолжаю рассказывать об упражнениях, улучшающих навык рисования, в данном случае геометрических фигур. Будем тренироваться рисовать их двухмерное отображение, трехмерное отображение и затенение фигур. Итак, Упражнения для рисования. Часть 2. Приступим.

Но прежде, чем приступить к упражнениям, напоминаю, что есть первая часть упражнений, посвященная линиям и штрихам.

Двумерные фигуры

Круг. Сначала будет сложно нарисовать ровный красивый круг, поэтому поможем себе с помощью циркуля. Легкой линией нарисуем окружность и обведем ее. Один раз, потом еще, запоминаем характер движения и пытаемся воспроизвести. Можно помогать себе проставив несколько точек для начала. Со временем, если выполнять это упражнение, круги будут получаться все лучше и краше. 🙂

Треугольник. Пробуем нарисовать равносторонний треугольник. Опять же, чтобы себе помочь для начала можем нарисовать окружность с помощью циркуля и уже в нее вписать нашу фигуру. Но потом обязательно пробуем нарисовать самостоятельно.

Квадрат. Да, сложно с первого раза нарисовать все стороны одинаковыми и все углы 90 градусов. Поэтому, чтобы запомнить правильную форму используем линейку. Потом рисуем по точкам, а потом самостоятельно, без вспомогательных инструментов.

После квадрата рисуем ромб, то есть тот же квадрат, но повернутый на 45 градусов.

Рисуем 5-конечную звезду, рисуем не отрывая карандаш от бумаги. Для первого раза можно воспользоваться циркулем и вписать звезду в окружность, чтобы добиться симметрии.

Шестиконечная звезда. Рисуется как 2 равносторонних треугольника.

Восьмиконечная звезда. Рисуется как 2 квадрата.

Яйцо. Это овал, который на одном конце уже, чем на другом.

Полумесяц. Эту фигуру нарисовать не так просто, как может показаться на первый взгляд. Сначала попробуйте нарисовать его самостоятельно, а потом уже при помощи циркуля, помня, что месяц это фактически часть двух пересекающихся окружностей.

Трехмерные фигуры

Переходим к трехмерным фигурам. Начнем с куба. Рисуем квадрат, потом еще один квадрат чуть выше и правее, соединяем углы ровными линиями. Получаем прозрачный куб. Теперь попробуем нарисовать тот же куб, но уже без видимых линий внутри.

Теперь рисуем куб в другом ракурсе. Для этого сначала рисуем плоский параллелограмм в форме ромба, опускаем них перпендикуляры и рисуем такую же фигуру в основании. И такой же куб, но без видимых линий.

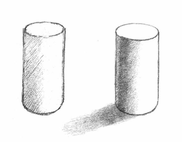
Теперь попробуем нарисовать цилиндр в разных ракурсах. Первый цилиндр будет прозрачный, рисуем овал, опускаем вертикали вниз и рисуем овал-основание. Затем рисуем цилиндр с невидимой нижней внутренней гранью и цилиндр с невидимой верхней внутренней гранью.

И завершаем этот цикл фигур рисованием конуса в разных ракурсах.

Трехмерные фигуры и тени

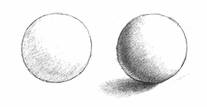
Рисуем круг. Намечаем легкой штриховкой тень в левом нижнем углу. Тень должна быть в форме полумесяца. Далее добавляем тона в тень при помощи большего нажима на карандаш, затеняем от центра к краю по принципу от светлого к темному, при этом у границы круга оставляем небольшой участок более светлой тени, это рефлекс. Дальше затеняем падающую тень, чем дальше от основания шара, тем светлее. Тень находится с противоположной от источника света стороны. То есть в нашем случае источник света находится в верхнем правом углу.

Теперь затеняем куб. В данном случае свет также находится в верхнем правом углу, а значит самая темная тень будет с противоположной стороны, сверху тени не будет, а правая видимая грань будет иметь более светлый тон. Соответственно с этим и наносим штриховку.

По такому же принципу затеняем стороны на кубе и конусе, важно следить за формой объекта и тем, как на него ложится свет. И падающая тень также должна соответствовать форме объекта.

И еще, в упражнениях для затенения используется диагональная штриховка, но я бы советовала пробовать в дальнейшем штриховать по форме объекта, тогда объект будет более объемный. Но штриховка по форме, да и вообще штриховка — тема довольно обширная, я уже начала ее изучать и скажу, что без тренировки рук и ровного быстрого штриха тут никуда, так что даже если делать только то, что я уже выложила, делать регулярно, то рисунки неизбежно будут становиться все лучше.

Видео:Шестиугольник в изометрииСкачать

Способы построения изометрической проекции плоских фигур, геометрических тел и деталей

Для выполнения изометрической проекции любой детали не­обходимо знать правила построения изометрических проекций плоских и объемных геометрических фигур.

Правила построения изометрических проекций геометриче­ских фигур. Построение любой плоской фигуры следует начи­нать с проведения осей изометрических проекций.

При построении изометрической проекции квадрата (рис. 109) из точки О по аксонометрическим осям откладывают в обе сто­роны половину длины стороны квадрата. Через полученные за­сечки проводят прямые, параллельные осям.

При построении изометрической проекции треугольника (рис. 110) по оси X от точки 0 в обе стороны откладывают отрезки, равные половине стороны треугольника. По оси У от точки О откладывают высоту треугольника. Соединяют полученные за­сечки отрезками прямых.

Рис. 109. Прямоугольная и изометрические проекции квадрата

Рис. 110. Прямоугольная и изометрические проекции треугольника

При построении изометрической проекции шестиугольника (рис. 111) из точки О по одной из осей откладывают (в обе сторо­ны) радиус описанной окружности, а по другой — H/2. Через полученные засечки проводят прямые, параллельные одной из осей, и на них откладывают длину стороны шестиугольника. Со­единяют полученные засечки отрезками прямых.

Рис. 111. Прямоугольная и изометрические проекции шестиугольника

Рис. 112. Прямоугольная и изометрические проекции круга

При построении изометрической проекции круга (рис. 112) из точки О по осям координат откладывают отрезки, равные его радиусу. Через полученные засечки проводят прямые, парал­лельные осям, получая аксонометрическую проекцию квадрата. Из вершин 1, 3 проводят дуги CD и KL радиусом 3С. Соединяют точки 2 с 4, 3 с С и 3 с D. В пересечениях прямых получаются центры а и б малых дуг, проведя которые получают овал, заме­няющий аксонометрическую проекцию круга.

Используя описанные построения, можно выполнить аксоно­метрические проекции простых геометрических тел (табл. 10).

10. Изометрические проекции простых геометрических тел

Способы построения изометрической проекции детали:

1. Способ построения изометрической проекции детали от формообразующей грани используется для деталей, форма кото­рых имеет плоскую грань, называемую формообразующей; ши­рина (толщина) детали на всем протяжении одинакова, на боко­вых поверхностях отсутствуют пазы, отверстия и другие элемен­ты. Последовательность построения изометрической проекции заключается в следующем:

1) построение осей изометрической проекции;

2) построение изометрической проекции формообразующей грани;

3) построение проекций остальных граней посредством изо­бражения ребер модели;

Рис. 113. Построение изометрической проекции детали, начиная от фор­мообразующей грани

4) обводка изометрической проекции (рис. 113).

1. Способ построения изометрической проекции на основе по­следовательного удаления объемов используется в тех случаях, когда отображаемая форма получена в результате удаления из исходной формы каких-либо объемов (рис. 114).
2. Способ построения изометрической проекции на основе по­следовательного приращения (добавления) объемов применяется для выполнения изометрического изображения детали, форма которой получена из нескольких объемов, соединенных опреде­ленным образом друг с другом (рис. 115).
3. Комбинированный способ построения изометрической про­екции. Изометрическую проекцию детали, форма которой полу­чена в результате сочетания различных способов формообразо­вания, выполняют, используя комбинированный способ построе­ния (рис. 116).

Аксонометрическую проекцию детали можно выполнять с изображением (рис. 117, а) и без изображения (рис. 117, б) неви­димых частей формы.

Рис. 114. Построение изометрической проекции детали на основе последовательного удаления объемов

Рис. 115 Построение изометрической проекции детали на основе последовательного приращения объемов

Рис. 116. Использование комбинированного способа построения изометрической проекции детали

Рис. 117. Варианты изображения изометрических проекций детали: а — с изображением невидимых частей;
б — без изображения невидимых частей

Видео:Треугольная пирамида. Ортогональные и изометрическая проекции.Урок22.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Пирамида из бумаги своими руками. Схемы и способы изготовления

Видео:Как начертить конус в объемеСкачать

Как сделать объемные геометрические фигуры

Дети познают мир в процессе игры и творчества. Трехмерные фигуры, выполненные своими руками, помогут познакомиться с удивительной наукой — геометрией.

Примеры трафаретов и шаблонов можно скачать из Интернета и распечатать. Затем все фигуры вырезают и склеивают. Дети старшего возраста могут самостоятельно нарисовать развертку нужной фигуры, малышам помогают родители,.

Геометрические объекты делают из бумаги (белой или цветной), картона. Из последнего материала они получаются плотными и прочными.

Из бумаги

к оглавлению ^

Из картона

к оглавлению ^

Развертки куба

Треугольника

Прямоугольника

Цилиндра

к оглавлению ^

Ромба

к оглавлению ^

Призмы

Видео:Как начертить ПРИЗМУ ТРЕХГРАННУЮСкачать

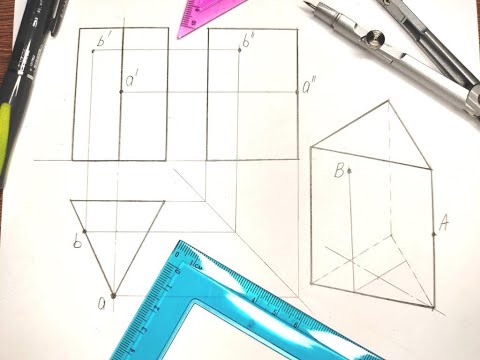
Задание 2 (построение прямоугольного треугольника)

Постройте на нелинованной бумаге треугольник , чтобы угол был прямым, длина стороны равнялась 15 см, а длина сторогы – 20 см.

Построим точку (Рис. 18).

Проведем через точку прямую (Рис. 19).

Рис. 19. Прямая, проведенная через точку

Для построения прямого угла воспользуемся прямоугольным треугольником. Приложим треугольник так, чтобы вершина прямого угла совпала с точкой , а одна из сторон совпала с лучом, как показано на рис. 20.

Рис. 20. Построение прямого угла

Проведем по второй стороне прямого угла треугольника луч из точки и получим прямой угол (Рис. 21).

Рис. 21. Полученный прямой угол

Выполним построение сторон треугольника. Построим отрезок , который равен 15 см (Рис. 22).

Построим отрезок , который равен 20 см (Рис. 23).

Соединим полученные точки отрезком . Мы получили прямоугольный треугольник (Рис. 24) с прямым углом и сторонами см и см.

Рис. 24. Треугольник

Видео:Как начертить ПИРАМИДУ в объемеСкачать

Схемы для вырезания

Ученикам 1–2 класса демонстрируют в школе простые геометрические фигуры и 3d: квадрат, кубик, прямоугольник. Их несложно вырезать и склеить. Шаблоны развивают мелкую моторику у детей и дают первые представления о геометрии.

Ученики средней школы, которые изучают черчение, делают сложные фигуры: бумажные шестигранники, фигуры из пятиугольников, цилиндры. Из бумаги для детей выполняют домики для кукол, мебель, оригами, замок для маленьких игрушек, маски на лицо (трехмерные называются полигональными).

Конуса

Пирамиды

Шестигранника

Макета с припусками

к оглавлению ^

Параллелепипеда

Трапеции

Овала

к оглавлению ^

Материал, из чего можно сделать плотный шар — картон или плотная бумага.

Многогранника

Параллелограмма

к оглавлению ^

Видео:Как начертить ПРИЗМУ ШЕСТИГРАННУЮ в объемеСкачать

Задание 1 (определение вида треугольников)

Назовите номера тупоугольных, остроугольных и прямоугольных треугольников на рисунке 16.

Рис. 16. Иллюстрация к заданию 1

Треугольник номер 1 – остроугольный, у него все углы острые. Треугольники номер 3 и 4 – тупоугольные, каждый из них имеет один тупой угол. Фигура номер 2 – прямоугольный треугольник. Проверим, действительно ли эта фигура имеет прямой угол, с помощью прямоугольного треугольника (Рис. 17).

Рис. 17. Проверка треугольника номер 2

Мы видим, что вершины и стороны прямого угла совпали, значит, угол прямой, а треугольник прямоугольный.

Видео:Треугольная пирамида. Проекции точек на гранях. Сечение. Урок23.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Шаблоны для склеивания

Зачастую школьники задаются вопросом, что можно сделать из бумаги к урокам труда или на выставку. Работы ученика выделятся среди остальных, если это будут сложные трехмерные предметы, рельефные геометрические фигуры, платоновы тела, шаблоны кристаллов и минералов.

Если следовать инструкции, то ученик 5–6 класса сможет без помощи родителей сделать точный додекаэдр или тетраэдр.

Иногда в школе задают логические задания, как из квадрата сделать круг или шестиугольник. Для этого определить центр квадрата, согнув его по диагонали. Точка пересечения прямых — центр квадрата и будущего круга. Исходя из этого, можно начертить круг.

Сложных фигур

к оглавлению ^

к оглавлению ^

Октаэдра

Тетраэдра

Икосаэдра

Додекаэдра

Гексаэдра

к оглавлению ^

Фигурок из треугольников

к оглавлению ^

Видео:Черчение. 8 класс. Мазаева И.М. Изометрия и ДиметрияСкачать

Виды углов

Развернутый угол. (Рис. 4)

Угол называется развернутым, если его стороны лежат на одной прямой.

Рис. 4. Виды углов: развернутый

Прямой угол (Рис. 5)

Прямой угол составляет половину развернутого.

Рис. 5. Виды углов: прямой угол

Прямой угол можно получить путем складывания бумаги. Сложив лист дважды, мы получим модель прямого угла, его составляют линии сгиба.

Приложим модель угла к углу на чертеже (Рис. 5) таким образом, чтобы углы и стороны совпали (Рис. 6).

Мы убедились, что на чертеже действительно изображен прямой угол.

Для удобства определения, прямой угол или нет, используют особый инструмент – прямоугольный треугольник (Рис. 7).

Рис. 7. Прямоугольный треугольник

Непрямые углы делятся на острые (Рис. и тупые (Рис. 11).

Рис. 10. Сравнение острого и прямого угла

Рис. 11. Виды углов: тупой угол

Тупой угол больше прямого (Рис. 12).

Рис. 12. Сравнение тупого и прямого угла

Видео:Построение треугольника в трёх проекцияхСкачать

Макеты из бумаги

Макетирование — увлекательное занятие. Оно помогает развить воображение и логическое мышление. Из бумаги делают не только фигуры, но и необычные скульптуры, статуэтки, шестиугольные–двенадцатиугольные предметы, наклонные объекты (например, Пизанскую башню), карандаши, линейки. На фото и картинках можно посмотреть, как выглядят оригинальные поделки из бумаги.

Школьники младших классов или дошколята делают бумажные объемные поделки. Например, предметы из овала — веер, цветы, гусеницы. Для них потребуются овалы и круги разного диаметра. Раскладки склеиваются между собой, получаются трехмерные игрушки.

Оригами

к оглавлению ^

Животные

к оглавлению ^

Корабль

Применяется множество вариантов, как сделать кораблик из бумаги.

к оглавлению ^

Полигональные чертежи

к оглавлению ^

Игрушки из фигур

к оглавлению ^

Геометрические маски

Карандаш

к оглавлению ^

🔍 Видео

Как нарисовать пирамиду?Скачать

Как начертить аксонометрию. Наглядный пример. Уроки черчения.Скачать

2 2 1 изометрия по чертежуСкачать

Как начертить овал. Эллипс вписанный в ромбСкачать

Как начертить треугольник | 4 способа | Выпуклый многоугольникСкачать

Построить проекции линии и точек на ней по заданным координатам. Начертательная геометрияСкачать

ПИРАМИДА в ИЗОМЕТРИИСкачать

Шестиугольная пирамида.Ортогональные и изометрическая проекции.Урок31.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать