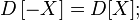Мат ожидание случайного вектора

В этом разделе рассмотрены числовые характеристики только двумерных случайных величин, поскольку обобщение на случай 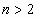не вызывает затруднений.

Пусть ( x , h ) — двумерная случайная величина, тогда M( x , h )=(M( x ), M( h )), т.е. математическое ожидание случайного вектора — это вектор из математических ожиданий компонент вектора.

Если ( x , h ) — дискретный случайный вектор с распределением

то математические ожидания компонент вычисляются по формулам:

, .

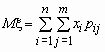
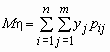
Эти формулы можно записать в сокращенном виде.

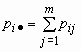
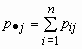
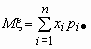
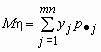
Обозначим и , тогда и .

Если p_{( x , h )}(x, y)- совместная плотность распределения непрерывной двумерной случайной величины ( x , h ), то

и .

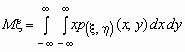
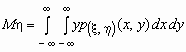
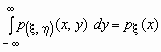
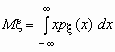
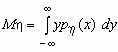
Поскольку -плотность распределения случайной величины x , то и, аналогично, .

Понятие дисперсии обобщается на многомерные случайные величины нетривиальным образом. Это обобщение будет сделано в следующем разделе. Здесь лишь приведем формулы для вычисления дисперсии компонент двумерного случайного вектора.

Если ( x , h ) — двумерная случайная величина, то

D x = M( x — M x ) 2 = M x 2 — M( x ) 2 , D h = M( h — M h ) 2 = M h 2 — M( h ) 2 .

Входящие в эту формулу математические ожидания вычисляются по приведенным выше формулам.

Между случайными величинами может существовать функциональная зависимость. Например, если x — случайная величина и h = x 2 , то h — тоже случайная величина, связанная с x функциональной зависимостью. В то же время между случайными величинами может существовать зависимость другого рода, называемая стохастической. В разделе, посвященном условным распределениям уже обсуждалась такая зависимость. Из рассмотренных там примеров видно, что информация о значении одной случайной величины (одной компоненты случайного вектора) изменяет распределение другой случайной величины (другой компоненты случайного вектора), а это может, вообще говоря, изменить и числовые характеристики случайных величин.

Математическое ожидание, вычисленное по условному распределению, называется условным математическим ожиданием.

Для двумерного дискретного случайного вектора ( x , h ) с распределением

условное математическое ожидание случайной величины x при условии, что случайная величина h принимает значение y_j, вычисляется по формуле .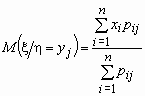

Аналогично, условное математическое ожидание случайной величины h при условии, что случайная величина x принимает значение x_i, равно .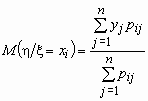

Видно, что условное математическое ожидание случайной величины x является функцией значений случайной величины h , т.е. M( x / h = y) = f₁(y) и, совершенно аналогично, M( h / x = x) = f₂(x).

Функцию f₁(y) называют регрессией случайной величины x на случайную величину h , а f₂(x) — регрессией случайной величины h на случайную величину x .

Если p_{( x , h )}(x, y) совместная плотность вероятностей двумерной случайной величины ( x , h ), то

и .

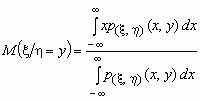
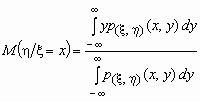
Если между случайными величинами x и h существует стохастическая связь, то одним из параметров, характеризующих меру этой связи является ковариация cov( x , h ). Ковариацию вычисляют по формулам cov( x , h )=M[( x — M x )( h — M h )] = M( x h ) — M x M h .

Если случайные величины x и h независимы, то cov( x , h )=0.

Обратное, вообще говоря, неверно. Из равенства нулю ковариации не следует независимость случайных величин. Случайные величины могут быть зависимыми в то время как их ковариация нулевая! Но зато, если ковариация случайных величин отлична от нуля, то между ними существует стохастическая связь, мерой которой и является величина ковариации.

cov( x , x ) = D x ;

;

;

,

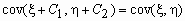
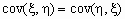
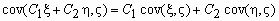
Ковариационной матрицей случайного вектора ( x , h ) называется матрица вида

.

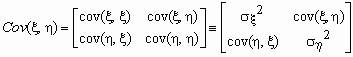
Эта матрица симметрична и положительно определена. Ее определитель называется обобщенной дисперсией и может служить мерой рассеяния системы случайных величин ( x , h ).

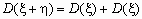
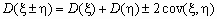
Как уже отмечалось ранее, дисперсия суммы независимых случайных величин равна сумме их дисперсий: . Если же случайные величины зависимы, то .

Понятно, что значение ковариации зависит не только от “тесноты” связи случайных величин, но и от самих значений этих величин, например, от единиц измерения этих значений. Для исключения этой зависимости вместо ковариации используется безразмерный коэффициент корреляции .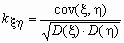

Этот коэффициент обладает следующими свойствами:

его модуль не превосходит единицы, т.е. ;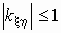

если x и h независимы, то k_{( x , h )}=0 (обратное неверно!);

если 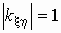, то случайные величины x и h связаны функциональной зависимостью вида

где a и b- некоторые числовые коэффициенты;

;

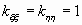
Корреляционной матрицей случайного вектора называется матрица

.

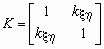
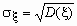
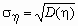
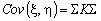
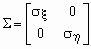
Если и , то ковариационная и корреляционная матрицы случайного вектора ( x , h ) связаны соотношением , где .

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Видео:Математическое ожидание-3 типа задачСкачать

Мат ожидание случайного вектора

Раздел 7. Многомерные случайные величины. Случайные функции

Пусть имеется пространство элементарных событий U, на нем построено поле событий и для каждого события А из этого поля определена вероятность Р(А). Каждому элементарному событию g_i из U сопоставим несколько чисел: ξ _i1 , ξ _i2 , ξ _i3 , . ξ _ik или вектор ξ_i . Потребуем, чтобы для любых х_j ( -∞ ξ называется многомерной случайной величиной , или случайным вектором , а F( x₁, x₂, . x_k ) ее функцией распределения .

Примеры:
1 . Координаты молекулы, находящейся в сосуде с газом, (x,y,z) или компоненты ее скорости (Vx,Vy,Vz) — можно рассматривать как трехмерные случайные величины
2 . В задаче «о встрече» время прихода одного участника (х₁) и другого (х₂), если условия их прихода известны (скажем — любой момент в течение заданного часа), пару чисел х₁, х₂ можно рассматривать как двумерную случайную величину
3 . Результат эксперимента, состоящего в измерении тока через разрядную трубку при десяти различных напряжениях, поданных на трубку, можно рассматривать как десятимерную случайную величину

Свойства многомерной функции распределения:
1 . F( x₁, x₂, . -∞ . x_k ) = 0;
2 . F( x₁, x₂, . x_k-1, ∞) = F( x₁, x₂, . x_k-1 ), т.е. если один из аргументов принимает значение ∞, то размерность случайной величины уменьшается на 1;
3 . F( x₁, x₂, . x_k ) не убывающая функция любого аргумента.

Многомерные случайные величины могут быть непрерывными , т.е. принимать любые значения в некоторой области к-мерного пространства (например, упомянутые выше компоненты скорости молекулы). У них F( x₁, x₂, . x_k ) непрерывная функция всех аргументов. Для них определена к-мерная плотность распределения p( x₁, x₂, . x_k ), которая есть производная от функци распределения.

(7.1)

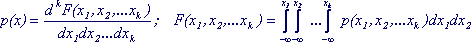
Вероятность того, что случайный вектор примет значение, лежащее в области V к-мерного пространства, равна интегралу по этой области от к-мерной плотности распределения.
Интеграл по всем переменным от — ∞ до + ∞ от к-мерной плотности распределения равен 1.

Интеграл по одной переменной от — ∞ до + ∞ от к-мерной плотности распределения равен плотности распределения (к-1)-мерной случайной величины.

(7.2)

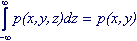
Многомерные случайные величины могут быть дискретными , т.е. каждая компонента случайного вектора может принимать только конечное или счетное множество определенных значений.
Например, рассмотрим эксперимент по бросанию одновременно двух костей, с каждым элементарным событием свяжем два числа ( z₁, z₂ ), где z₁ — число очков на первой кости, z₂ — сумма очков на двух костях. Тогда ( z₁, z₂ ) — двумерная случайная величина, поскольку известна вероятность р( х_i, х_k ) пересечения событий, состоящих в том, что z₁ примет значение х_i, а z₂ — х_k . Для дискретных случайных величин закон распределения задается вероятностями всевозможных комбинаций их значений. Для двумерной величины при небольшом числе возможных значений это удобно представить в виде таблицы, где на пересечении столбца z₁ и строки z₂ стоит вероятность р( z₁, z₂ )

Таблица 7.1 Закон распределения двумерной величины z₁, z₂

Просуммировав все значения р( z₁, z₂ ) вдоль каждой строки, мы получим вероятности определенных значений z₂ , т.е. закон распределения одномерной величины z₂ . Аналогично, сумма по столбцам даст закон распределения одномерной величины z₁ . Сумма всех чисел в таблице должна быть равна 1 .

Математическим ожиданием многомерной случайной величины называется вектор, компоненты которого являются математическим ожиданием каждой отдельной компоненты случайного вектора.
M( z₁, z₂, . z_k ) = ( Mz₁, Mz₂, . Mz_k ). Mz_i вычисляются как сумма или интеграл так же, как и для одномерных случайных величин . (см. раздел 6)

Дисперсия многомерной случайной величины описывается ковариационной матрицей .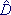
Это таблица чисел размерности К×К для К-мерной величины, у которой на диагонали стоят дисперсии соответствующих одномерных величин, вычисляемых обычным образом, а ij-тым элементом является b_ij — коэффициент ковариации i-той и j-той компоненты случайного вектора.

(7.3)

Коэффициент ковариации случайных величин z_i , z_j , обозначаемый иногда как cov(z_i,z_ji), есть математическое ожидание произведения отклонений каждой из этих величин от своего математического ожидания:

Для вычисления коэффициента ковариации надо знать закон распределения двумерной случайной величины (z_i,z_j). Тогда для непрерывных величин:

(7.5)

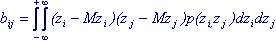
для дискретных величин:

(7.6)

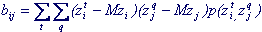
Здесь суммирование ведется по всем t значениям, которые принимает величина z_i и всем q значениям, которые принимает величина z_j .

Преобразовав (7.4), получим более удобную формулу для вычисления коэффициента ковариации

Вычислим характеристики двумерной величины, представленной в таблице 7.7

Мz₁ = 1/6 &#215( 1 + 2 + 3 + 4 + 5 + 6 ) = 3.5
Мz₂ = 2/36 + 3/18 + 4/12 + 5/9 + 30/36 + 7/6 + 40/36 + 9/9 + 10/12 + 11/18 + 12/36 = 7 , т.е.
М(z₁, z₂) = (3.5, 7)

Dz₁ = 1/6 ×( 1 + 4 + 9 + 16 + 25 + 36 ) — 3.52 = 3.417
Dz₂ = 4/36 + 9/18 + 16/12 + 25/9 + 36 × (5/36) + 49/6 + 64 × (5/36) + 81/9 + 100/12 + 121/18 + 144/36 — 49 = 5.833

M(z₁z₂) = 1/36 × (1×2 + 1×3 + 1×4 + 1×5 + 1×6 + 1×7 + 2×3 + 2×4 + 2×5 + 2×6 + 2×7 + 2×8 + 3×4 + 3×5 + 3×6 + 3×7 + 3×8 + 3×9 + 4×5 + 4×6 + 4×7 + 4×8 + 4×9 + 4×10 + 5×6 + 5×7 + 5×8 + 5×9 + 5×10 + 5×11 + 6×7 + 6×8 + 6×9 + 6×10 + 6×11 + 6×12) — 3.5×7 = 2.917 ,

т.е. ковариационная матрица имеет вид:

(7.7)

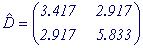
Часто используется понятие: коэффициент корреляции r_ij — это коэффициент ковариации, деленный на корень из произведения дисперсий i-той и j-той компонент случайного вектора

(7.8)

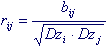
Коэффициент корреляции r_ij может быть положительным или отрицательным, но никогда по модулю не превосходит 1.

Компоненты многомерной случайной величины называются независимыми , если многомерная функция распределения, многомерная плотность распределения, вероятность определенного набора значений распадаются на произведение соответствующих одномерных функций или вероятностей:

Условия (7.9), а также вытекающее из них и определения условной вероятности условия, которые должны выполняться во всей области существования значений случайных величин:

— признаки независимости случайных величин

Компоненты z₁, z₂ двумерной величины, представленной в таблице 7.7, не независимы, т.к. p(1,4) = Р<z₁ = 1, z₂ = 4> = 1/36 ,
P<z₁ = 1> = 1/6 ,
P<z₂ = 4> = 1/12 (условие 7.9 нарушено);

p(1/10) = Р<z₁ = 1/z₂ = 10> = 0 ,
P<z₁ = 1> =1/6 ( условие 7.10 нарушено);

Для независимых случайных величин:

Коэффициенты ковариации и корреляции равны 0, следовательно, ковариационная матрица — диагональна

Математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий.

Дисперсия суммы независимых случайных величин равна сумме их дисперсий

Понятие о случайной функции (случайном процессе)

Если элементарному событию сопоставляется не набор чисел ( случайный вектор), как в разделе 7, а функция некоторого параметра t — f(t) и при каждом значении t определена функция распределения F t (x)=P<f(t) случайной функцией или случайным процессом . Образно говоря — это "бесконечномерная случайная величина".

Если F t (x) не зависит от t, процесс называется стационарным . Числовые характеристики случайного процесса (математическое ожидание и дисперсия) при фиксированном t определяются так же, как и для обычной случайной величины , если известны плотность распределения р t (х) или р t (x i ) (если f принимает дискретный ряд значений). Для стационарного процесса эти характеристики от t не зависят.

Для стационарного процесса статистические характеристики модно вычислить и по другому- путем усреднения по параметру :

(7.11)

(7.12)

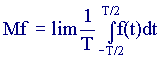
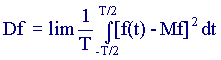
Если оба способа вычисления числовых характеристик дают одинаковый результат, процесс называется эргодическим.

Аналогом ковариационной матрицы, которая характеризует связь между компонентами случайного вектора, для случайного процесса служит автокорреляционная функция Г(τ), показывающая как быстро с изменением параметра могут меняться значения случайной функции.

(7.13)

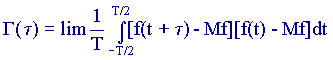
Видео:Случайный вектор двумерной случайной величиныСкачать

Математическое ожидание случайного вектора

Диспе́рсия случа́йной величины́ —мера разброса данной случайной величины, то есть её отклонения от математического ожидания.

Свойства:

Дисперсия любой случайной величины неотрицательна

-Если дисперсия случайной величины конечна, то конечно и её математическое ожидание;

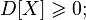
-Если случайная величина равна константе, то её дисперсия равна нулю: Верно и обратное: если то 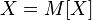почти всюду;

-Дисперсия суммы двух случайных величин равна:

где — их ковариация;

-Для дисперсии произвольной линейной комбинации нескольких случайных величин имеет место равенство:

-В частности, для любых независимых или некоррелированных случайных величин, так как их ковариации равны нулю;

—

—

—

8 (Биномиальное, нормальное, равномерное распределение. Распределе­ние Пуассона.)

Биномиа́льное распределе́ние в теории вероятностей — распределение количества «успехов» в последовательности из n независимых случайных экспериментов, таких, что вероятность «успеха» в каждом из них постоянна и равна p .

Функция распределения биномиального распределения может быть записана в виде суммы:

Нормальное распределение, также называемое распределением Гаусса — распределение вероятностей, которое в одномерном случае задается функцией плотности распределения:

Таким образом, одномерное нормальное распределение является двухпараметрическим семейством распределений. Многомерный случай описан в многомерном нормальном распределении.Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1. Значение: Важное значение нормального распределения во многих областях науки, например, в математической статистике и статистической физике вытекает из центральной предельной теоремы теории вероятностей. Если результат наблюдения является суммой многих случайных слабо взаимозависимых величин, каждая из которых вносит малый вклад относительно общей суммы, то при увеличении числа слагаемых распределение центрированного и нормированного результата стремится к нормальному. Этот закон теории вероятностей имеет следствием широкое распространение нормального распределения, что и стало одной из причин его наименования. Непреры́вное равноме́рное распределе́ние — в теории вероятностей — распределение случайной вещественной величины, принимающей значения, принадлежащие интервалу [a, b], характеризующееся тем, что плотность вероятности на этом интервале постоянна.

Функция распределения

Так как плотность равномерного распределения разрывна в граничных точках отрезка , то функция распределения в этих точках не является дифференцируемой. В остальных точках справедливо стандартное равенство:

Распределение Пуассона — вероятностное распределение дискретного типа, моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга. Распределение Пуассона играет ключевую роль в теории массового обслуживания.

Дата добавления: 2015-01-30 ; просмотров: 11 | Нарушение авторских прав

🔍 Видео

Математика без Ху!ни. Ряд распределения дискретной случайной величины. Мат ожидание и дисперсия.Скачать

Математическое Ожидание, Дисперсия, Стандартное Отклонение за 5 минутСкачать

Теория вероятностей #12: случайная величина, плотность и функция распределенияСкачать

Функция распределения дискретной случайной величиныСкачать

Функция распределения непрерывной случайной величины. Вероятность попадания в интервалСкачать

Функция распределения и плотность распределенияСкачать

Корреляция и ковариация двумерной случайной величиныСкачать

Теория вероятностей #18: системы двух случайных величин, двумерное распределениеСкачать

Лекция 14. Мат.ожидание суммы случайного количества сл.в. Нормальный сл.вектор.Скачать

Теория вероятностей #14: математ. ожидание, дисперсия, медиана, мода, начальные моментыСкачать

Непрерыный случайный вектор и его характеристикиСкачать

Математическое ожидание дискретной случайной величины. 10 класс.Скачать

Свойства математического ожидания и дисперсииСкачать

Математическое ожидание и дисперсия непрерывной случайной величиныСкачать

Математическое ожидание дискретной случайной величиныСкачать

2.8. Совместное распределение двух случайных величин.Скачать

Двумерное дискретное распределениеСкачать

Теория вероятностей #19: ковариация, корреляция, зависимость двух случайных величинСкачать