Боковые стороны равнобедренного треугольника 544

Боковые стороны равнобедренного треугольника равны 544, основание равно 512. Найдите радиус вписанной окружности.

Это задание ещё не решено, приводим решение прототипа.

Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.

Радиус вписанной окружности равен отношению площади к полупериметру. Для нахождения площади, воспользуемся формулой Герона:

Тогда

Приведем решение Лены Кисловой.

Радиус вписанной окружности равен отношению площади к полупериметру. Для нахождения площади найдем высоту равнобедренного треугольника:

тогда

Тогда

Видео:ГДЗ по геометрии | Номер 544, 545 Геометрия 8 класс Атанасян Л.С. | Подробный разборСкачать

Боковые стороны равнобедренного треугольника 544

Вопрос по математике:

Боковые стороны равнобедренного треугольника равны 544,
основание равно 512. Найдите радиус вписанной окружности.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Пишите, если что не так.

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.

Видео:Задание № 544 — Геометрия 8 класс (Атанасян)Скачать

Основание ac равнобедренного треугольника abc равно 10 окружность радиуса

Видео:№544. Из квадрата, диагональ которого равна d, свернута боковая поверхность цилиндра.Скачать

Основание ac равнобедренного треугольника abc равно 10 окружность радиуса

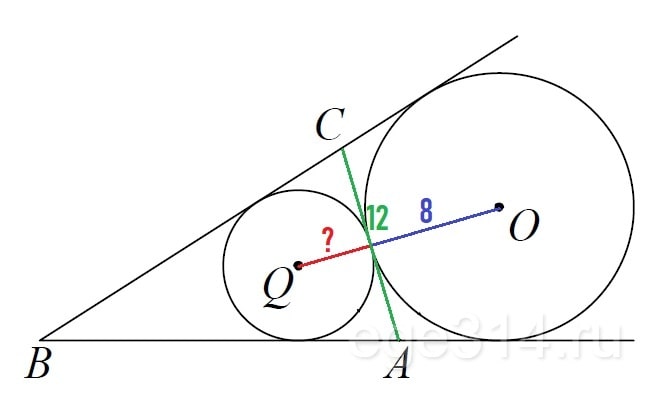
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 7,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.

Данная окружность касается стороны AC в её середине M и продолжений сторон BA и BC треугольника ABC.

Пусть O — центр этой окружности, а Q — центр окружности, вписанный в треугольник ABC. Угол OAQ — прямой как угол между биссектрисами смежных углов. Треугольник OAQ — прямоугольный, AM — его высота. Из этого треугольника находим, что . Следовательно, .

Ответ: .

Видео:Геометрия Боковые стороны равнобедренного треугольника равны 4, радиус описанной окружности равенСкачать

Основание AC равнобедренного треугольника ABC равно 10?

Математика | 5 — 9 классы

Основание AC равнобедренного треугольника ABC равно 10.

Окружность радиуса 6 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине.

Найдите радиус окружности, вписанной в треугольник ABC.

Ответ округлите до сотых.

Мой вариант решения смотри на фотографии.

Видео:16 заание ОГЭ . 16.3.4. Равнобедренные треугольникиСкачать

Боковые стороны равнобедренного треугольника равны 544, основание равно 512?

Боковые стороны равнобедренного треугольника равны 544, основание равно 512.

Найдите радиус вписанной окружности.

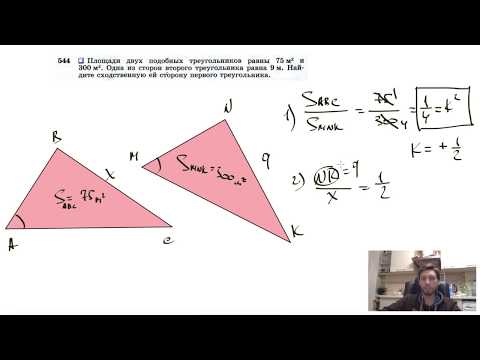
Видео:№544. Площади двух подобных треугольников равны 75 м2 и 300 м2. Одна из сторон второгоСкачать

В равнобедренном треугольнике высота, проведенная к основанию равна 5 см, а угол при основании равен 30 * ?

В равнобедренном треугольнике высота, проведенная к основанию равна 5 см, а угол при основании равен 30 * .

Найдите боковую сторону треугольника, площадь треугольника и радиус вписанной окружности.

Написать дано сделать чертеж.

Видео:Задание №544 - ГДЗ по геометрии 7 класс (Мерзляк)Скачать

Основание равнобедренного треугольника равно 8, радиус вписанной окружности равен 2?

Основание равнобедренного треугольника равно 8, радиус вписанной окружности равен 2.

Найдите площадь треугольника.

Видео:2080 Боковые стороны равнобедренного треугольника равны 569 основание равно 462Скачать

Основание равнобедренного треугольника равно 6, а радиус вписанной окружности 2?

Основание равнобедренного треугольника равно 6, а радиус вписанной окружности 2.

Найти боковую сторону треугольника.

Видео:№163. Докажите, что середины сторон равнобедренного треугольника являются вершинами другого равнобедСкачать

Основание равнобедренного треугольника равно 16 см, боковая сторона равна 17 см?

Основание равнобедренного треугольника равно 16 см, боковая сторона равна 17 см.

Найдите радиус вписанной в этот треугольник окружности.

Видео:Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Высота bd проведенная к основанию равнобедренного треугольника abc = 4 а боковая сторона = 5 найдите радиусы вписанной и описаной окружности?

Высота bd проведенная к основанию равнобедренного треугольника abc = 4 а боковая сторона = 5 найдите радиусы вписанной и описаной окружности.

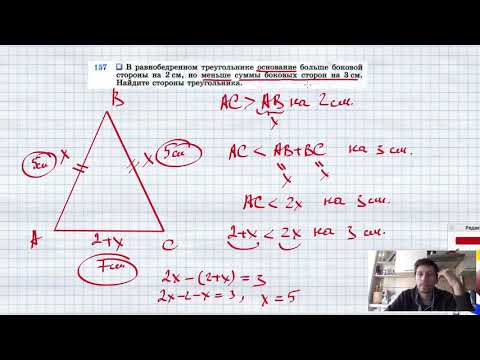
Видео:№157. В равнобедренном треугольнике основание больше боковой стороны на 2 см, но меньше суммы боковыСкачать

Высота BD, проведенная к основанию равнобедренного треугольника ABC = 4, а боковая сторона = 5?

Высота BD, проведенная к основанию равнобедренного треугольника ABC = 4, а боковая сторона = 5.

Найдите радиусы вписанной и описаной окружности.

Видео:№107. В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметрСкачать

В окружность вписан равнобедренный треугольник ABC с основанием BC?

В окружность вписан равнобедренный треугольник ABC с основанием BC.

Найдите ∠ A треугольника ABC, если ⌣AC = 96 градусов.

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

В равнобедренном треугольнике основание равно 10 см , а боковая сторона равна 13 см ?

В равнобедренном треугольнике основание равно 10 см , а боковая сторона равна 13 см .

Найдите радиус окружности , вписанной в этот треугольник.

Видео:Боковая сторона равнобедренного треугольника равна 5 ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

В равнобедренном треугольнике основание равно 10см , а боковая сторона равна 13см ?

В равнобедренном треугольнике основание равно 10см , а боковая сторона равна 13см .

Найдите радиус окружности , вписанной в этот треугольник.

Вы перешли к вопросу Основание AC равнобедренного треугольника ABC равно 10?. Он относится к категории Математика, для 5 — 9 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Математика. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.

Он спрятал в второй норке 45.

84 — 39 = 45 (горошин) — во второй норке.

Качество прекрасное, если правильно разглядела, то : 1) — 3( — 5 + 5х) + 3х = — 6 15 — 15х + 3х = — 6 — 12х = — 21 х = 21 / 12 х = 1, 75 2) 4 — 9( — 5 + 9х) = — 10х — 9 4 + 45 — 81х = — 10х — 9 — 71х = — 58 х = 58 / 71 3) 7х + 2( — 7 + 5х) = — 8х — 2..

5х — 18 = 7х + 12 переносим х и обычные числа 5х — 7х = 18 + 12 — 2х = 30 сокращаем — х = 15 х = — 15.

5x — 18 = 7x + 12 5x — 7x = 12 + 18 — 2x = 30 x = 30 / — 2 x = — 15.

29 (целое число — это все натуральные числа, все противоположные им по знаку и ноль.

29 чисел. От — 14 до 0 14 чисел и от 0 до 14 — 14 чисел. Ну и 0.

Видео:Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

Решение №655 Основание AC равнобедренного треугольника ABC равно 12.

Основание AC равнобедренного треугольника ABC равно 12. Окружность радиусом 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания AC. Найдите радиус окружности, вписанной в треугольник ABC.

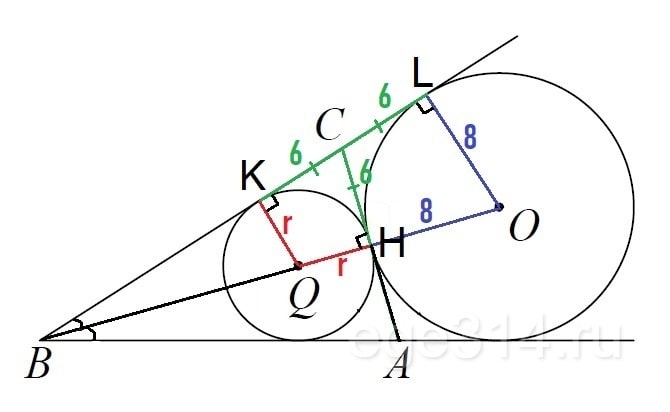
О – центр не вписанной окружности, Q – центр вписанной окружности, по условию получаем рисунок:

Достроим ОВ, которая является биссектрисой равнобедренного ΔАВС, а значит и медианой ⇒ CH = AH = 12/2 = 6. Достроим радиусы QK и OL к касательной DC. Радиус и касательная всегда пересекаются под прямым углом.

По свойству отрезков касательных к окружности проведённых из одной точки CH = CK = CL = 6.
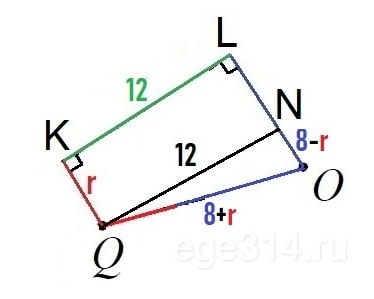
Обозначим радиус вписанной окружности – r. LOQK – прямоугольная трапеция, проведём в ней высоту и рассмотрим ΔNQO.

Сторона ON = KL = 12, как противоположные стороны прямоугольника. OQ = 8 + r, это сумма радиусов. NO = 8 – r. Треугольник прямоугольный, через теорему Пифагора найдём r:

QN 2 + ON 2 = OQ 2
12 2 + (8 – r) 2 = (8 + r) 2
144 + 64 – 16r + r 2 = 64 + 16r +r 2
– 16r + r 2 – 16r – r 2 = 64 – 144 – 64
– 32r = – 144
r = – 144/( – 32) = 4,5

💡 Видео

7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

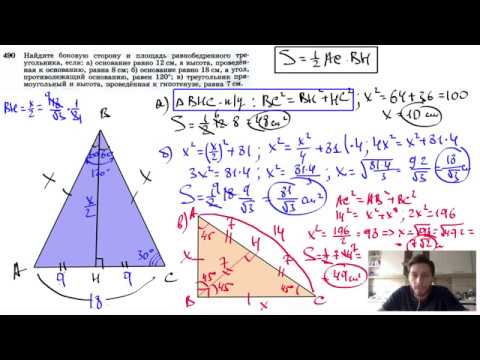
№490. Найдите боковую сторону и площадь равнобедренного треугольника, если: а) основание равноСкачать

Задача 6 №27923 ЕГЭ по математике. Урок 140Скачать

Задача 6 №27900 ЕГЭ по математике. Урок 128Скачать

№487. Боковая сторона равнобедренного треугольника равна 17 см, а основание равно 16 смСкачать