Масса вектор или нет (3 видео) | Курс школьной геометрии

Какая величина является векторной, а какая скалярной? Просто о сложном

Пугающие школьника два слова — вектор и скаляр — на самом деле не являются страшными. Если подойти к теме с интересом, то все можно понять. В данной статье рассмотрим, какая величина является векторной, а какая скалярной. Точнее, приведем примеры. Каждый ученик, наверное, обращал внимание, что в физике некоторые величины обозначаются не только символом, но и стрелкой сверху. Что они обозначают? Об этом будет сказано ниже. Постараемся разобраться, чем отличается векторная величина от скалярной.

Содержание

Примеры векторов. Как они обозначаются
Положительные и отрицательные величины
Векторная или скалярная величина?
Вектор и скаляр в формулах
Два определения массы, и почему я использую только одно из них
Имеет ли частица света, фотон, массу или нет?
Действительно ли масса электрона больше, чем масса атомного ядра?
Есть ли масса у нейтрино?
У всех ли частиц одного типа – к примеру, у всех фотонов, у всех электронов, у всех протонов, у всех мюонов – одинаковая масса?
Истинна ли старая формула Ньютона F = ma, соотносящая массу, воздействие и ускорение?
Увеличивается ли масса частицы с увеличением скорости и энергии?
youinf.ru
Векторная масса или масса двумерна?
🎬 Видео

Видео:Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

Примеры векторов. Как они обозначаются

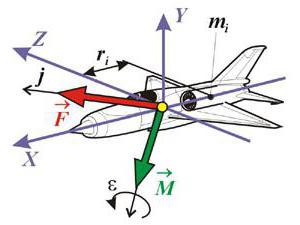
Что подразумевается под вектором? То, что характеризует движение. Не важно, в пространстве или на плоскости. Какая величина является векторной вообще? Например, летит самолет с определенной скоростью на какой-то высоте, имеет конкретную массу, начал движение из аэропорта с нужным ускорением. Что относится к движению самолета? Что заставило его лететь? Конечно, ускорение, скорость. Векторные величины из курса физики являются наглядными примерами. Говоря прямо, векторная величина связана с движением, перемещением.

Вода тоже движется с определенной скоростью с высоты горы. Видите? Движение осуществляется за счет не объема или массы, а именно скорости. Теннисист дает возможность мячику двигаться при помощи ракетки. Он задает ускорение. К слову сказать, приложенная в данном случае сила также является векторной величиной. Потому что она получается вследствие заданных скоростей и ускорений. Сила способна также меняться, осуществлять конкретные действия. Ветер, который колышет листья на деревьях, тоже можно считать примером. Так как имеется скорость.

Видео:Математика это не ИсламСкачать

Положительные и отрицательные величины

Векторной величиной называется величина, которая имеет направление в окружающем пространстве и модуль. Снова появилось пугающее слово, на этот раз модуль. Представьте, что нужно решить задачку, где будет фиксироваться отрицательное значение ускорения. В природе отрицательных значений, казалось бы, не существует. Как скорость может быть отрицательной?

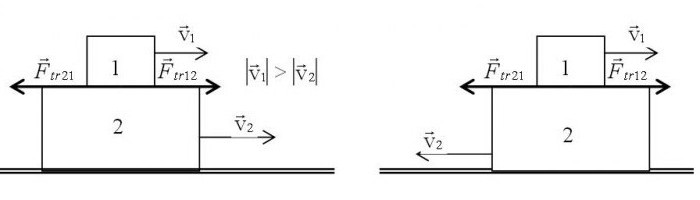
У вектора есть такое понятие. Это касается, например, сил, которые приложены к телу, но имеют разные направления. Вспомните третий закон Ньютона, где действие равно противодействию. Ребята перетягивают канат. Одна команда в синих футболках, вторая — в желтых. Вторые оказываются сильнее. Допустим, что вектор их силы направлен положительно. В то же время у первых не получается натянуть канат, но пытаются. Возникает противодействующая сила.

Видео:Физика | Ликбез по векторамСкачать

Векторная или скалярная величина?

Поговорим о том, чем отличается векторная величина от скалярной. Какой параметр не имеет никакого направления, но имеет свое значение? Перечислим некоторые скалярные величины ниже:

время (секунда, минута, день, год);
масса (грамм, килограмм, тонна);
длина, расстояние (сантиметр, метр, километр);
площадь и объем (метр квадратный и кубический);
температура (градус Цельсия, Фаренгейт);
доза радиации, излучения (бар, рентген);
уровень шума, вибрации (децибел).

Имеют ли все они направление? Нет. Какая величина является векторной, а какая скалярной, можно показать только наглядными примерами. В физике есть такие понятия не только в разделе «Механика, динамика и кинематика», а так же в параграфе «Электричество и магнетизм». Сила Лоренца, индукция, магнитное поле — все это так же векторные величины.

Видео:ПОЧЕМУ KRISS VECTOR НЕ ИМЕЕТ ОТДАЧИСкачать

Вектор и скаляр в формулах

В учебниках по физике часто встречаются формулы, в которых есть стрелочка сверху. Вспомните второй закон Ньютона. Сила («F» со стрелочкой сверху) равна произведению массы («m») и ускорения («a» со стрелочкой сверху). Как говорилось выше, сила и ускорение являются величинами векторными, а вот масса — скалярной.

К сожалению, не во всех изданиях есть обозначение этих величин. Наверное, сделано это для упрощения, чтобы школьников не вводить в заблуждение. Лучше всего покупать те книги и справочники, в которых обозначены векторы в формулах.

То, какая величина является векторной, покажет иллюстрация. Рекомендуется обращать внимание на картинки и схемы на уроках физики. Векторные величины имеют направление. Куда направлена сила тяжести? Конечно же, вниз. Значит, стрелочка будет показана в том же направлении.

В технических вузах изучают физику углубленно. В рамках многих дисциплин преподаватели рассказывают о том, какие величины являются скалярными и векторными. Такие знания требуются в сферах: строительство, транспорт, естественные науки.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Два определения массы, и почему я использую только одно из них

К сожалению, в процессе революции в науке, происходившей с понятиями пространства, времени, энергии, импульса и массы, Эйнштейн, кроме прочего, оставил после себя два различных и противоречащих друг другу определения массы. Из-за этого всё, что мы говорим и имеем в виду, можно интерпретировать двумя очень разными способами. При этом непосредственно в физике никакой путаницы нет. Специалисты точно знают, о чём идёт речь, и знают, как делать предсказания и использовать подходящие уравнения. Весь вопрос только в значении самого слова. Но слова важны, особенно когда мы беседуем о физике с людьми, не являющимися экспертами в этой области, и с учениками, для которых уравнения пока ещё не полностью понятны.

В своих статьях под «массой» я имею в виду свойство объекта, которое иногда ещё называют «инвариантной массой» или «массой покоя». Для нас с моими коллегами по физике частиц это просто старая добрая «масса». Термины «инвариантная масса» или «масса покоя» используются для того, чтобы уточнить, что вы имеете в виду под «массой», только если вы настаиваете на введении второй величины, которую вы тоже хотите называть «массой», и которую обычно называют «релятивистской массой». Специалисты по физике частиц избегают этой путаницы, совсем не используя концепцию «релятивистской массы».

Масса покоя лучше релятивистской в том, что первая масса – это свойство, по поводу величины которого соглашаются все наблюдатели. У объектов не так уж много подобных свойств. Возьмём скорость объекта: разные наблюдатели не согласятся по поводу скорости. Вот едет машина – как быстро она едет? С вашей точки зрения, если вы стоите на дороги, допустим, она едет со скоростью 80 км/ч. С точки зрения водителя машины она не двигается, а двигаетесь вы. С точки зрения человека, едущего навстречу машине, она может двигаться уже со скоростью в 150 км/ч. Выходит, что скорость – величина относительная. Нет смысла спрашивать о скорости машины, ибо нельзя получить ответ. Вы должны спрашивать, какова скорость объекта относительно определённого наблюдателя. У каждого наблюдателя есть право сделать это измерение, но разные наблюдатели получат разные результаты. Принцип относительности Галилея уже включал в себя эту идею.

Зависимость от наблюдателя применима и к энергии, и к импульсу. Она применяется и к релятивистской массе. Это оттого, что релятивистская масса равна энергии, делённой на константу – а именно, с 2 — поэтому, если вы определите массу как «релятивистскую», тогда разные наблюдатели разойдутся во мнениях по поводу массы объекта m, хотя все согласятся, что E = mс 2 .

Но масса покоя, которую я называю просто «массой», не зависит от наблюдателя, поэтому её иногда называют инвариантной массой. Все наблюдатели соглашаются по поводу массы объекта m, определённой таким образом. И все наблюдатели согласятся, что если вы покоитесь относительно объекта, измеренная вами его энергия будет равна mс 2 , а в ином случае энергия будет отличаться в большую сторону. Итого: с определением массы, используемой мною в статьях,

• Если скорость объекта относительно наблюдателя v=0, тогда наблюдатель измерит, что у объекта E = mc 2 и импульс p = 0.
• Если вместо этого объект двигается относительно наблюдателя, то он измерит, что E > mc 2 , и импульс тоже больше нуля (p > 0).
• В общем случае соотношения между E, p, m и v задаются двумя уравнениями:
o v = pc/E
o
• что согласуется с двумя предыдущими утверждениями, ибо, если p=0, тогда v=0 и (следовательно, E = mc 2 ), а если p>0, тогда v>0 и (поскольку pc > 0) E должно быть больше, чем mc 2

Эти уравнения и их графическое представление подробно разобраны в другой статье.

Мне хочется дать вам понять причины, по которым специалисты по физике частиц используют эти уравнения и не считают, что уравнение E = mc 2 всегда выполняется. Это уравнение относится к тому случаю, в котором наблюдатель не двигается по отношению к объекту. Я попытаюсь сделать это, задав несколько вопросов, ответы на которых сильно различаются в зависимости от выбора значения слова «масса». Это поможет привлечь ваше внимание к большим проблемам в случае существования двух соперничающих определений массы и пояснить, почему в физике частиц гораздо проще работать с массой, не зависящей от наблюдателя.

Имеет ли частица света, фотон, массу или нет?

Если вы используете моё определение массы – то нет. Фотон – частица безмассовая, поэтому его скорость всегда равна универсальному пределу скорости с. А вот электрон массой обладает, поэтому его скорость всегда меньше с. Масса всех электронов составляет 0.000511 ГэВ/c 2 .

Но если вы имеете в виду релятивистскую массу – тогда да, имеет. У фотона всегда есть энергия, поэтому у него всегда есть масса. Ни один наблюдатель не увидит его безмассовым. Нулевая у него только инвариантная масса, также известная, как масса покоя. У каждого электрона будет своя масса, и у каждого фотона будет своя. Электрон и фотон, обладающие одной энергией, будут по этому определению обладать одной массой. У некоторых фотонов масса будет больше, чем у некоторых электронов, а у других электронов масса будет больше, чем у других фотонов. Что ещё хуже, для одного наблюдателя масса определённого электрона будет больше массы определённого фотона, а для другого всё может быть наоборот! Поэтому релятивистская масса приводит к путанице.

Действительно ли масса электрона больше, чем масса атомного ядра?

Если вы используете моё определение массы – то нет, никогда. Все наблюдатели согласятся с тем, что масса электрона в 1800 раз меньше массы протона или нейтрона, из которых состоит ядро.

Но если под массой подразумевать релятивистскую, то ответ будет: это зависит от ситуации. Масса электрона в покое меньше. У очень быстрого электрона – больше. Можно даже устроить всё таким образом, что масса электрона будет в точности совпадать с массой выбранного ядра. В общем можно сказать только то, что масса покоя электрона меньше, чем масса покоя ядра.

Есть ли масса у нейтрино?

При использовании моего понятия массы, ответ на этот вопрос был неизвестен с 1930-х годов, когда впервые была предложена концепция нейтрино, до 1990-х. Сегодня нам известно (почти наверняка), что у нейтрино масса есть.

Но если под массой подразумевать релятивистскую, то ответ будет: естественно, мы знали об этом с самого первого дня существования понятия «нейтрино». У всех нейтрино есть энергия, так что, как и у фотонов, у них есть масса. Вопрос лишь в наличии инвариантной массы.

У всех ли частиц одного типа – к примеру, у всех фотонов, у всех электронов, у всех протонов, у всех мюонов – одинаковая масса?

При использовании моего понятия массы, ответ на этот вопрос будет утвердительным. Все частицы одного типа обладают одинаковой массой.

Но если под массой подразумевать релятивистскую, то ответ будет: очевидно, нет. Два электрона, движущихся с разными скоростями, обладают разной массой. У них одинаковая только инвариантная масса.

Истинна ли старая формула Ньютона F = ma, соотносящая массу, воздействие и ускорение?

При использовании моего понятия массы, ответ будет: нет. В эйнштейновской версии относительности эта формула исправлена.

Но если под массой подразумевать релятивистскую, то ответ будет: это зависит от ситуации. Если вектора сила и движения частицы перпендикулярны, тогда да; в ином случае – нет.

Увеличивается ли масса частицы с увеличением скорости и энергии?

При использовании моего понятия массы, ответ будет: нет. Смотрите график выше. Разные наблюдатели могут назначить частице разную энергию, но все согласятся с её массой.

Но если под массой подразумевать релятивистскую, то ответ будет: да. Разные наблюдатели могут назначить частице разную энергию, и, следовательно, разные массы. Согласятся они только по поводу инвариантной массы.

Итак, мы по меньшей мере видим наличие лингвистической проблемы. Если мы не обозначим точно, какое из определений массы мы используем, мы получим совершенно разные ответы на простейшие вопросы физики. К сожалению, в большинстве книг для непрофессионалов и даже в некоторых учебниках для первого курса университета (!) авторы переключаются туда и сюда между этими терминами без пояснений. И самая распространённая путаница среди моих читателей связана с тем, что им сообщают два типа сведений о массе, противоречащих друг другу: один подходит для массы покоя, другой – для релятивистской. Очень плохо использовать одно слово для двух разных вещей.

Это, конечно, всего лишь язык. С языком можно делать всё, что угодно. Определения и семантика не имеют значения. Когда физик вооружён уравнениями, язык становится неидеальным носителем. Математика никогда не путается, и человек, понимающий математику, тоже не запутается.

Но для большинства людей и для начинающих студентов это кошмар.

Что делать? Один вариант – настаивать на использовании всех возможных терминов. Но из-за этого объяснения будут очень запутанными.

• Энергия покоящегося объекта = инвариантной массе умноженной на с 2 = релятивистской массе умноженной на с 2
• Масса движущегося объекта = инвариантной массе, как и раньше, но энергия = релятивистской массе помноженной на с 2 у него больше, чем ранее, из-за энергии движения.

Это слишком многословно. Мы с коллегами просто говорим:

• У покоящегося объекта массы m энергия E равна mс 2 ,
• а у движущегося объекта масса всё ещё равна m, а энергия E больше, чем mс 2 , ровно на энергию движения.

Такой способ не менее содержателен, в нём используется меньше различных концепций и определений, он избегает двух противоречивых значений слова «масса», одно из которых не меняется с движением, а другое – меняется.

С точки зрения лингвистики, семантики и концепций, необходимо избегать понятия «релятивистская масса» и убрать слова «инвариантная» и «покоя» из определений «инвариантная масса» и «масса покоя» потому, что «релятивистская масса» – бесполезная концепция. Это просто другое название для энергии частицы. Использовать понятие «релятивистской массы» – это то же самое, как настаивать на термине «красновато-синий». Если я начну настаивать на использовании термина «красновато-синий» для описания изюма, вы возразите: но у нас уже есть слово для этого цвета: пурпурный. Что с ним не так? И ещё вы можете сказать: «Говорить, что цвет изюма – это разновидность синего цвета, неправильно и это запутывает. Можно сделать вывод, что цвет изюма немного похож на цвет неба, а на самом деле они отличаются». Примерно в таком же ключе релятивистская масса помноженная на с 2 — это просто другое название энергии (для которой у нас уже есть подходящее слово), и описывать энергию так, будто это что-то вроде массы, значит, запутывать читателя.

Вот ещё одна причина, по которой называть энергию формой массы плохо. В уравнениях Эйнштейна пространство и время связаны вместе так же, как энергия и импульс. Вы даже можете вспомнить, что энергия сохраняется из-за независимости законов физики от времени, а импульс – из-за независимости законов от места. Поэтому, если мы говорим, что масса – это E/c 2 , то что такое p/c? Оно же должно что-то обозначать. Что именно? Но никто не дал этой величине имя. Почему? Потому, что «импульс» – хорошее название для p, и для p/c имя не нужно. Так почему же «энергия» не подходит для E? Зачем нам новое название для E/c 2 ? Особенно, если учесть, что в уравнении с E и p появляется ещё одна величина:

Величина справа явно не нуждается в новом названии, поскольку это явно ни E, ни p – она не сохраняется, как E и p, но она не зависит от наблюдателя (в отличие от E и p!)

Понятие «релятивистской массы» появилось не на пустом месте и не из какой-то глупости. Его ввёл сам Эйнштейн, и не зря, поскольку он имел дело с отношениями между энергией системы объектов и массой этой системы. Но хотя понятие релятивистской массы пропагандировалось и распространялось другими знаменитыми физиками того времени, сам Эйнштейн, судя по всему, отбросил такой способ мышления, и тоже не зря. Так же поступило сообщество современных специалистов по физике частиц.

В статьях и исследованиях я никогда не использую релятивистскую массу. Я использую вместо неё энергию, поскольку для частицы самой по себе релятивистская масса – это просто энергия, делённая на c 2 . И под «массой» я всегда подразумеваю «инвариантную массу», или «массу покоя», на которой сходятся все наблюдатели. Масса электрона всегда равна 0,000511 ГэВ/c 2 , неважно, с какой скоростью он движется. Масса любого электрона меньше массы атомного ядра. Все фотоны в пустоте всегда безмассовые. А масса частиц Хиггса равна 125 ГэВ/c 2 , вне зависимости от их скорости. Специалисты по физике частиц пользуются такой лингвистической и концептуальной договорённостью. Это не обязательно, вы можете сделать другой выбор. Но такой подход позволяет избегать множества практических и концептуальных проблем, что я и пытался здесь показать.

Видео:Ваша масса не зависит от бозона Хиггса [Veritasium]Скачать

youinf.ru

Видео:Урок 62. Сила тяжести и вес тела. Невесомость.Скачать

Векторная масса или масса двумерна?

У нас масса двумерна. Я вам предлогаю самим задуматься. Масса Планка (максима, планковская масса) — единица массы в планковской системе единиц. Частица с такой массой имеет гравитационный радиус в разы меньше комптоновской длины волны ≈ 1,2209·1019 ГэВ/c² = 2,176·10−8 кг.

Мне кажется, что тут что-то не так. Как деформировать планковскую величину? В трехмерном мире? Остается главным вопросом …. Если всё же из трехмерного мира можно создать двумерный, то каким образом его увидят в трехмерном. Одна из пространственных координат 0, существование плоскости равно 0. Духмерный мир 0. Если одно из измерений стремиться к 0. Побудим в этот момент наблюдающими и от третьего лица, мысленно остановим время, все процессы, чтоб разобрать все по полочкам. А время имеет планковскую величину, так как существуют путешественники во времени, не так ли? Значит можно зафиксироваться на планковской величине времени, то есть остановить его. Остановили. Мы пришли к первому. Одно из измерений 0 и существование плоскости 0.

Ни капли рождения вселенной из логики, а логический вывод с собственной точки зрения, глядя на происходящее. Между тем я лишь брал все из интернета и вставил свои ”умозаключения”, кто из вас умнее и поможет объяснить мою неправоту. Взаимодействие = взаимоотношение, у кого голова есть, поймет. У меня есть гипотеза… Но, возможно там будет не совсем понятно почему именно в форме шара получаются звезды. Я её после подправлю…

Почему в невесомости капли воды принимают шарообразную форму? Если взять давление элементарных частиц, то сил движений окажется меньше между молекулами, чем вне них. А первое, что получается в космосе после волчка, это плазменный шар с магнитным полем. А по моей гипотезе это частицы темной материи, которые при столкновении получают вращательное движение, а значит волновое колебание квинтэссенции, то есть их объём для взаимодействий увеличился, а значит для них темная материя становится потоком более мелких частиц.