Магнитное поле играет очень большую роль в электротехнике и электронике. Без магнитного поля не функционировали бы герконы, электромагнитные реле, соленоиды, катушки индуктивности, дроссели, трансформаторы, двигатели, динамики, генераторы электрической энергии да и вообще много чего.
- Природа магнетизма
- Магнитные линии и магнитный поток
- Напряженность магнитного поля
- Формула напряженности
- Напряженность магнитного поля проводника с током
- Магнитное поле проводника с током
- Соленоид
- Магнитное поле кругового тока
- Применение закона Био – Савара – Лапласа к вычислению магнитного поля кругового тока
- Готовые работы на аналогичную тему
- Магнитное поле кругового тока в его центре
- Кольца Гельмгольца
- Магнитное поле дуги окружности
- 📽️ Видео
Видео:Дуга в магнитном полеСкачать

Природа магнетизма
Согласно одной из легенд, когда-то давным-давно жил в Греции пастух по имени Магнес. И вот шел он как-то со своим стадом овец, присел на камень и обнаружил, что конец его посоха, сделанный из железа, стал притягиваться к этому камню. С тех пор стали называть этот камень магнетит в честь Магнеса. Этот камень представляет из себя оксид железа.
Если такой камень положить на деревянную доску на воду или подвесить на нитке, то он всегда выстраивался в определенном положении. Один его конец всегда показывал на СЕВЕР, а другой — на ЮГ.
Этим свойством камня пользовались древние цивилизации. Поэтому, это был своего рода первый компас. Потом уже стали обтачивать такой камень и делать из разные фигурки. Например, так выглядел китайский древний компас, ложка которого была сделана из того самого магнетита. Ручка у этой ложки всегда показывала на ЮГ.
Ну а далее дело шло за практичностью и маленькими габаритами. Из магнетита вытачивали маленькие стрелки, которые подвешивали на тонкую иглу посередине. Так стали появляться первые малогабаритные компасы.
Древние цивилизации, конечно, не знали еще что такое север и юг. Поэтому, одну сторону магнетита они назвали северным полюсом (North), а противоположный конец — южным (South). Названия на английском очень легко запомнить, если кто смотрел американский мультфильм «Южный парк», он же Сауз (South) парк).
Видео:Дуга в магнитном полеСкачать

Магнитные линии и магнитный поток
Вокруг магнита экспериментальным путем были обнаружены магнитные силовые линии. Эти магнитные линии создают так называемое магнитное поле.
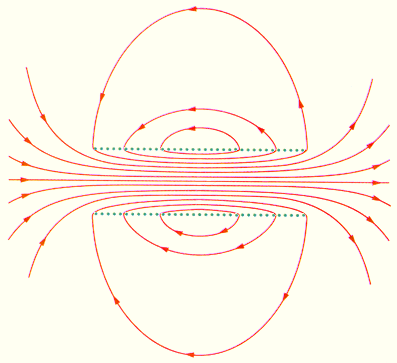
Как вы могли заметить на рисунке, концентрация магнитных силовых линий на самых краях магнита намного больше, чем в его середине. Это говорит о том, что магнитное поле является более сильным именно на краях магнита, а в его середине практически равна нулю. Направлением магнитных силовых линий считается направление от севера к югу.
Ошибочно считать, что магнитные силовые линии начинают свое движение от северного полюса и заканчивают свой век на южном. Это не так. Магнитные линии — они замкнуты и непрерывны. В магните это будет выглядеть примерно так.
Если приблизить два разноименных полюса, то произойдет притягивание магнитов
Если же приблизить одноименными полюсами, то произойдет их отталкивание
Итак, ниже важные свойства магнитных силовых линий.
- Магнитные линии не поддаются гравитации.
- Никогда не пересекаются между собой.
- Всегда образуют замкнутые петли.
- Имеют определенное направление с севера на юг.
- Чем больше концентрация силовых линий, тем сильнее магнитное поле.
- Слабая концентрация силовых линий указывает на слабое магнитное поле.
Магнитные силовые линии, которые образуют магнитное поле, называют также магнитным потоком.
Итак, давайте рассмотрим два рисунка и ответим себе на вопрос, где плотность магнитного потока будет больше? На рисунке «а» или на рисунке «б»?
Видим, что на рисунке «а» мало силовых магнитных линий, а на рисунке «б» их концентрация намного больше. Отсюда можно сделать вывод, что плотность магнитного потока на рисунке «б» больше, чем на рисунке «а».
В физике формула магнитного потока записывается как
Ф — магнитный поток, Вебер
В — плотность магнитного потока, Тесла
а — угол между перпендикуляром n (чаще его зовут нормалью) и плоскостью S, в градусах
S — площадь, через которую проходит магнитный поток, м 2
Что же такое 1 Вебер? Один вебер — это магнитный поток, который создается полем индукцией 1 Тесла через площадку 1м 2 расположенной перпендикулярно направлению магнитного поля.
Видео:Правило рук 👋 КАК ЛЕГКО определять НАПРАВЛЕНИЕ ЛИНИЙ МАГНИТНОГО ПОЛЯ??Скачать

Напряженность магнитного поля
Формула напряженности
Слышали ли вы когда-нибудь такое выражение: «напряженность между ними все росла и росла». То есть по сути напряженность — это что-то невидимое, какая-то сдерживающая сила, энергия. Здесь почти все то же самое. Напряженностью магнитного поля также часто называют силой магнитного поля. Напряженность магнитного поля напрямую зависит от плотности магнитного потока и выражается формулой
H — напряженность магнитного поля, Ампер/метр
B — плотность магнитного потока, Тесла
μ0 — магнитная постоянная = 4π × 10 -7 Генри/метр или если написать по человечески 1,2566 × 10 -6 Генри/метр.
Эта формула работает только тогда, когда между витками катушки находится воздух, либо вакуум. Более крутая формула выглядит вот так.
μ — это относительная магнитная проницаемость.
У разных веществ она разная
Напряженность магнитного поля проводника с током
Итак, имеем какой-либо проводник, по которому течет электрический ток.
Для того, чтобы вычислить напряженность магнитного поля на каком-то расстоянии от проводника при условии, что проводник находится в воздушном пространстве либо в вакууме, достаточно воспользоваться формулой
H — напряженность магнитного поля, Ампер/метр
I — сила тока, текущая через проводник, Ампер
r — расстояние до точки, в которой измеряется напряженность, метр
Видео:Билет №15 "Магнитное поле"Скачать

Магнитное поле проводника с током
Оказывается, если через какой-либо проводник пропустить электрический ток, то вокруг проводника образуется магнитное поле.
Здесь можно вспомнить знаменитое правило буравчика, но для наглядности я лучше буду использовать правило самореза, так как почти все хоть раз в жизни ввинчивали либо болт, либо саморез.
Ввинчиваем по часовой стрелке — саморез идет вниз. В нашем случае он показывает направление электрического тока. Движение наших рук показывает направление линий магнитного поля. Все то же самое, когда мы начинаем откручивать саморез. Он начинает вылазить вверх, то есть в нашем случае показывает направление электрического тока, а наша рука в этом время рисует в воздухе направление линий магнитного поля.
Также часто в учебниках физики можно увидеть, что направление электрического тока от нас рисуют кружочком с крестиком, а к нам — кружочком с точкой. В этом случае опять представляем себе саморез и уже в голове увидим направление магнитного поля.
Как думаете, что будет если мы сделаем вот такую петельку из провода? Что изменится в этом случае?
Давайте же рассмотрим этот случай более подробно. Так в этой плоскости оба проводника создают магнитное поле, то по идее они должны отталкиваться друг от друга. Но если они хорошо закреплены, то начинается самое интересное. Давайте рассмотрим вид сверху, как это выглядит.
Как вы можете заметить, в области, где суммируются магнитные силовые линии плотность магнитного потока прям зашкаливает.
Видео:МАГНИТНОЕ ПОЛЕ за 24 минуты. ЕГЭ Физика. Николай Ньютон. ТехноскулСкачать

Соленоид
А что если сделать много-много таких петелек? Взять какую-нибудь круглую бобину, намотать на нее провод и потом убрать бобину. У нас должно получится что-то типа этого.
Если подать постоянное напряжение на такую катушку, магнитные силовые линии будут выглядеть вот так.
Вы только посмотрите, какая бешеная плотность магнитного потока внутри такой катушки! Получается, что от каждой петельки магнитное поле суммируется, что в итоге дает такую плотность магнитного потока. Такую катушку также называют катушкой индуктивности или соленоидом.
Вот также схема, показывающая как магнитные силовые линии складываются в соленоиде.
Плотность магнитного потока зависит от того, какая сила тока проходит через соленоид. Чтобы увеличить плотность магнитного потока, достаточно поверх витков намотать еще больше витков и вставить сердечник из специального материала — феррита.
Если в электрических цепях есть такое понятие, как ЭДС — электродвижущая сила, то и в магнитных цепях есть свой аналог — МДС — магнитодвижущая сила. Магнитодвижущая сила выражается в виде тока, протекающего через катушку из N витков и выражается в Амперах-витках.
I — это сила тока в катушке, Амперы
N — количество витков катушки, штуки)
Также советую посмотреть очень простое и интересное видео про магнитное поле.
Похожие статьи по теме «магнитное поле»
Видео:Физика - Магнитное полеСкачать

Магнитное поле кругового тока
Вы будете перенаправлены на Автор24
Французские ученые Ж. Био и Ф. Савар изучали магнитные поля, создаваемые постоянными токами разной формы. Результаты их работы обобщил известный математик и физик П. Лаплас.
Видео:Дуга постоянного тока в магнитном полеСкачать

Применение закона Био – Савара – Лапласа к вычислению магнитного поля кругового тока
Закон Био-Савара–Лапласа описывает порождение магнитного поля током $I$ на элементе проводника длиной $dl$ в некоторой точке пространства ($mu$ — магнитная проницаемость вещества в котором локализовано поле):
где $d vec l ⃗$ — вектор, длина которого равна длине элемента проводника $dl$, направленный по току; $vec r$ – радиус-вектор, который проведен от элемента $dl$ в точку, в которой исследуется магнитное поле. Поскольку в правой части формулы (1) находится векторное произведение, очевидно, что индукция элементарного магнитного поля будет направлена перпендикулярно плоскости, в которой находятся векторы $vec r$ и $vec l$ и при этом является касательной к силовой линии поля.
Величину вектора $vec$ из выражения (1) найдем как:
где $ alpha $– угол между векторами $vec r$ и $vec l$ .
Конкретное направление $vec$ находят по правилу буравчика (правилу правой руки):
Если правый винт вращать так, что его поступательное движение будет совпадать с направлением течения тока в избранном элементе, то вращение его головки укажет направление $vec$.
Магнитные поля подчиняются принципу суперпозиции:
Суммарную магнитную индукцию поля, создаваемого несколькими источниками, находят как геометрическую сумму векторов магнитной индукции отдельных полей:
$vec=sumlimits_^N vec_ left( 3 right). $
Если распределение токов можно считать непрерывным, то принцип суперпозиции можно записать:
Вычисление магнитной индукции поля с применением закона Био-Савара-Лапласа довольно сложная процедура. Но при существовании определенной симметрии в распределении токов, используя, рассмотренный нами закон и принцип суперпозиции, рассчитать конкретные поля просто. В любом случае следует придерживаться следующей схемы действий:
Готовые работы на аналогичную тему
- Выделить на проводнике с током элементарный отрезок $dl$.
- Записать для исследуемой точки поля закон Био – Савара – Лапласа.
- Определить направление элементарного поля $vec$ в избранной точке.
- Воспользоваться принципом суперпозиции для магнитных полей (учесть, что суммируются векторы).
Видео:Урок 281. Электромагнитная индукция. Магнитный поток. Правило ЛенцаСкачать

Магнитное поле кругового тока в его центре
Рисунок 1. Магнитное поле кругового тока в его центре. Автор24 — интернет-биржа студенческих работ
Рассмотрим круговой проводник, по которому течет постоянный ток $I$ (рис.1). Выделим на этом проводнике элемент $dl$, который можно считать прямолинейным. Если перейти к другому элементу этого же тока, затем к третьему и так далее, применить правило правого винта, то очевидно, что все магнитные поля, созданные этими элементами в центре, направлены вдоль одной прямой, перпендикуляру к плоскости кольца. Это означает, применяя принцип суперпозиции, мы векторное сложение заменим алгебраическим.
Запишем закон Био-Савара-Лапласа для модуля вектора индукции поля, создаваемого элементом d$l_1$:
Из рис.1 мы видим:
- что расстояние от элементарного тока до центра витка равно его радиусу ($R$) и будет одинаковым для всех элементов на этом витке,
- элемент $dl$ (как и все остальные элементы) будут нормальны к радиус-вектору $vec r$.
Учитывая сказанное выражение (5) представим в виде:
Обезличивая витки с током, положим далее $dl_1=dl$.
Поскольку наш ток является непрерывным, то для нахождения полного поля в его центре, мы проинтегрируем (6), имеем:
$L=2πR$ — длина окружности витка.
Индукция магнитного поля кругового тока на его оси
Найдем индукцию магнитного поля на оси кругового тока, если ток, текущий по нему равен $I$, радиус витка — $R$ (рис.2).
Рисунок 2. Индукция магнитного поля кругового тока на его оси. Автор24 — интернет-биржа студенческих работ
Как основу для выполнения поставленной задачи возьмем закон Био-Савара-Лапласа (1), где из рис.2 мы видим, что:
$dvectimes vec=dvectimes vec+dvectimes vec(9).$
Используя принцип суперпозиции закон (1) для нашего тока и формулы (8-9) запишем:
В выражении (10) при записи интеграла, мы учли, что величина вектора $vec$ не изменяется. Кроме этого вектор $vec h$, определяющий положение точки, в которой мы ищем поле, не изменяется при движении по нашему контуру, поэтому:
$ointlimits_L <dvectimes vec> =(ointlimits_L <dvec)timesvec> =0, left( 11 right),$
так как ( $ointlimits_L <dvec)=0.>$
Вычислим интеграл: $ointlimits_L <dvectimes vec.>$ Введем единичный вектор ($vec n$), нормальный к плоскости витка с током.
$ointlimits_L <dvectimes vec=ointlimits_L <vecRdl=vecR>> ointlimits_L <dl=vecR> 2pi R=2pi R^vecleft( 12 right)$.
Подставляем результаты интегрирования из (12) в (10), имеем:
где при записи окончательного результата мы учли, что:
Видео:Математика это не ИсламСкачать

Кольца Гельмгольца
Кольцами Гельмгольца считают пару проводников в виде колец одного радиуса, расположенных в параллельных плоскостях (рис.3) на одной оси. Расстояние между плоскостями колец равно их радиусу.
Рисунок 3. Кольца Гельмгольца. Автор24 — интернет-биржа студенческих работ
Рассмотрим магнитное поле на оси этих колец.
Декартову систему координат разместим так, что ее начало совпадает с центром нижнего кольца с током. Ось Z нашей системы будет направлена по оси колец (рис.3).
Запишем индукцию магнитного поля в точке с координатой $z$ на оси колец. Используем формулу (13):
Исследуем полученное поле. Считается, что магнитное поле на оси колец Гельмгольца на посередине между ними является однородным.
Неоднородность в первом приближении характеризуют первой производной:
Если $z=fracquad$ , подставим в (15), имеем:
По условию для колец Гельмгольца, имеем: $d=R.$
На середине их общей оси ($z=frac)$, получаем:
Равенство нулю второй производной от $B_z$ по координате $z$, показывает, что в на середине оси колец магнитное поле является однородным с высокой степенью точности.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 28 03 2022
Видео:вращение электрической дуги в магнитном полеСкачать

Магнитное поле дуги окружности
Магнитное поле постоянных токов различной конфигурации изучалось экспериментально французскими учеными Ж. Био и Ф. Саваром (1820 г.). Они пришли к выводу, что индукция магнитного поля токов, текущих по проводнику, определяется совместным действием всех отдельных участков проводника. Магнитное поле подчиняется принципу суперпозиции :
Если магнитное поле создается несколькими проводниками с током, то индукция результирующего поля есть векторная сумма индукций полей, создаваемых каждым проводником в отдельности.
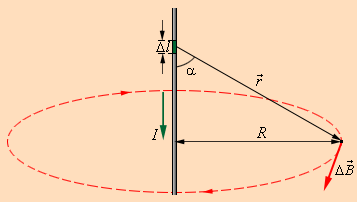
Индукцию 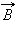
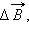
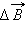
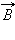
|
Здесь – расстояние от данного участка Δ до точки наблюдения, α – угол между направлением на точку наблюдения и направлением тока на данном участке, μ0 – магнитная постоянная. Направление вектора 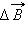
|
которая уже приводилась в § 1.16.
 | |||||||||||||||||||||||
| Рисунок 1.17.1. Закон Био–Савара позволяет рассчитывать магнитные поля токов различных конфигураций. Нетрудно, например, выполнить расчет магнитного поля в центре кругового витка с током. Этот расчет приводит к формуле
где – радиус кругового проводника. Для определения направления вектора Расчеты магнитного поля часто упрощаются при учете симметрии в конфигурации токов, создающих поле. В этом случае можно пользаоваться теоремой о циркуляции вектора магнитной индукции , которая в теории магнитного поля токов играет ту же роль, что и теорема Гаусса в электростатике. Поясним понятие циркуляции вектора
|


























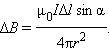
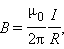
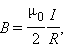
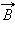 также можно использовать правило буравчика, только теперь его рукоятку нужно вращать в направлении кругового тока, а поступательное перемещение буравчика укажет направление вектора магнитной индукции.
также можно использовать правило буравчика, только теперь его рукоятку нужно вращать в направлении кругового тока, а поступательное перемещение буравчика укажет направление вектора магнитной индукции.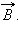 Пусть в пространстве, где создано магнитное поле, выбран некоторый условный замкнутый контур (не обязательно плоский) и указано положительное направление его обхода. На каждом отдельном малом участке Δ этого контура можно определить касательную составляющую
Пусть в пространстве, где создано магнитное поле, выбран некоторый условный замкнутый контур (не обязательно плоский) и указано положительное направление его обхода. На каждом отдельном малом участке Δ этого контура можно определить касательную составляющую 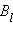 вектора
вектора 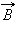 в данном месте, то есть определить проекцию вектора
в данном месте, то есть определить проекцию вектора 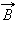 на направление касательной к данному участку контура (рис. 1.17.2).
на направление касательной к данному участку контура (рис. 1.17.2).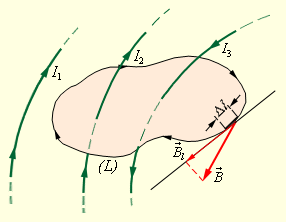
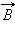 называют сумму произведений
называют сумму произведений 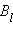 Δ, взятую по всему контуру :
Δ, взятую по всему контуру :
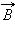 магнитного поля постоянных токов по любому контуру всегда равна произведению магнитной постоянной μ0 на сумму всех токов, пронизывающих контур:
магнитного поля постоянных токов по любому контуру всегда равна произведению магнитной постоянной μ0 на сумму всех токов, пронизывающих контур: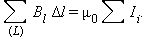
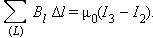
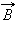 направлен по касательной
направлен по касательной 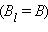 , а его модуль одинаков во всех точках окружности. Применение теоремы о циркуляции приводит к соотношению:
, а его модуль одинаков во всех точках окружности. Применение теоремы о циркуляции приводит к соотношению: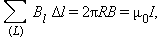
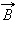 может быть использована для расчета магнитных полей, создаваемых симметричным распределением токов, когда из соображений симметрии можно «угадать» общую структуру поля.
может быть использована для расчета магнитных полей, создаваемых симметричным распределением токов, когда из соображений симметрии можно «угадать» общую структуру поля.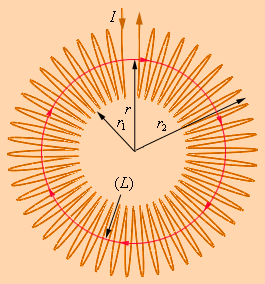
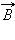 одинаков вдоль всей этой линии. По теореме о циркуляции можно записать:
одинаков вдоль всей этой линии. По теореме о циркуляции можно записать: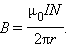
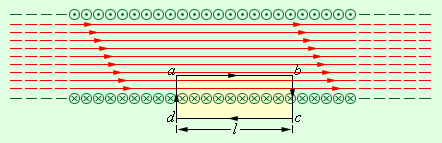
 по контуру равна , где – длина стороны . Число витков соленоида, пронизывающих контур , равно , где – число витков на единицу длины соленоида, а полный ток, пронизывающий контур, равен . Согласно теореме о циркуляции,
по контуру равна , где – длина стороны . Число витков соленоида, пронизывающих контур , равно , где – число витков на единицу длины соленоида, а полный ток, пронизывающий контур, равен . Согласно теореме о циркуляции,








