Рассмотрим задачи, в которых изображён круг на клетчатой бумаге и требуется по известной площади круга найти площадь заштрихованного сектора либо найти площадь круга по данному значению площади сектора.
Для решения обеих задач надо определить величину соответствующего ему центрального угла.
Градусная мера окружности — 360°. Зная центральный угол, найдем, какую часть площадь закрашенного сектора составляет от площади круга.
Самые простые задания этого вида — те, в которых центральный угол — прямой. 90° составляют четверть от 360°. Отсюда, для нахождения площади сектора площадь круга следует разделить на 4. И наоборот, для нахождения площади круга по известной площади сектора площадь сектора умножаем на 4.
Стороны прямого угла, чаще всего, либо проведены по клеточкам (одна сторона — горизонтально, другая — вертикально), либо делят каждую клеточку по диагонали (как диагональ квадрата).
Определить прямой угол можно даже с помощью листа бумаги (приложив его к центру круга).
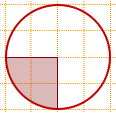
1) На клетчатой бумаге изображён круг площадью 60.
Найти площадь заштрихованного сектора.
Так как центральный угол, соответствующий данному сектору, равен 90º, то
2) На клетчатой бумаге изображён круг.
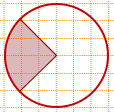
Какова площадь круга, если площадь заштрихованного сектора равна 17?
Так как стороны угла делят каждую клеточку по диагонали, образуя с горизонтальной прямой, проходящей из вершины угла, углы по 45°, то центральный угол равен 90º.
Следовательно, площадь сектора составляет 1/4 от площади круга: Sкруга=Sсектора:(1/4)=17·4=68.
3) Найти площадь круга, если площадь заштрихованного сектора равна 21.
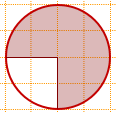
Площадь заштрихованного сектора составляет 3/4 площади круга.
Следовательно, чтобы найти площадь круга, надо площадь сектора разделить на 3/4:
4) Какова площадь круга если известно, что площадь закрашенного сектора равна 11?
Соответствующий центральный угол равен 45° (одно сторона угла проведена по горизонтали, другая делит каждую клеточку по диагонали (является диагональю квадрата).
Так как 45° составляет от 360° 1/8 часть, то
5) На клетчатой бумаге изображен круг площадью 96.
Найдите площадь заштрихованного сектора.
Центральный угол, соответствующий незакрашенной части, равен 45°, то есть составляет 1/8 площади круга.
Sзакрашенного сектора=Sнезакрашенного сектора-Sкруга=96-12=84.
А как определить на клетчатой бумаге центральные углы в 60° и 30°?
Можно рассуждать следующим образом.
Рассмотрим треугольник ABC.
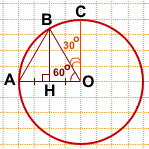
Так как BH — его высота и медиана, то ABC — равнобедренный с основанием AO. Значит, AB=BO.
Но AO=BO (как радиусы).
Следовательно, AB=BO=AO, то есть треугольник ABC — равносторонний. Следовательно, все его углы равны по 60°, в частности, ∠AOB=60°.
6) Найти площадь заштрихованного сектора, если площадь круга равна 30.
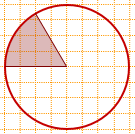
Соответствующий центральный угол равен 60°. Значит, площадь сектора составляет 1/6 от площади круга и Sсектора=Sкруга:6=30:6=5.
7) Найти площадь круга, если площадь заштрихованного сектора равна 24.
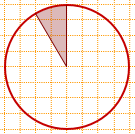
Так как центральный угол заштрихованного сектора равен 30°, то площадь сектора составляет 1/12 часть от площади круга.
8) Найти площадь круга, изображенного на клетчатой бумаге, если площадь заштрихованного сектора равна 60.
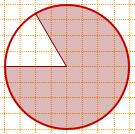
Центральный угол, соответствующий незакрашенному сектору, равен 60°. Значит, площадь незакрашенной части составляет 1/6 площади круга.
Следовательно, на площадь закрашенной части приходится 5/6 круга:
В некоторых случаях центральный угол можно найти как сумму или разность других центральных углов.
9) 
Центральный угол равен 30+45=75°,
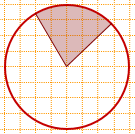
площадь заштрихованного сектора составляет
1/12+1/8=5/24 площади круга, то есть
10) Центральный угол равен 180-30=150°,
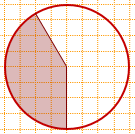
площадь заштрихованного сектора составляет 1/2-1/12=5/12 площади круга,
11) Центральный угол равен 60-45=15°,
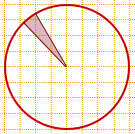
площадь заштрихованного сектора составляет 1/24 площади круга
12) Центральный угол равен 15+90=105°
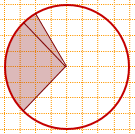
Видео:Окружность. 7 класс.Скачать
Урок математики в 6-м классе по теме «Окружность. Круг. Длина окружности»
Разделы: Математика
Демонстрационный материал: циркуль, материал для опыта: предметы круглой формы и верёвочки (на каждого ученика) и линейки; модель круга, цветные мелки.
Цель: Изучение понятия «окружность» и ее элементов, установление связи между ними; введение новых терминов; формирование умения проводить наблюдения и с помощью экспериментальных данных делать выводы; воспитание познавательного интереса к математике.
I. Организационный момент
Приветствие. Постановка цели.
III. Новый материал
Среди всевозможных плоских фигур выделяются две главные: треугольник и окружность. Эти фигуры известны вам с раннего детства. Как дать определение треугольника? Через отрезки! А как же определить что такое окружность? Ведь эта линия в каждой точке изгибается! Известный математик Гратендик, вспоминая свои школьные годы, заметил, что увлёкся математикой после того, как узнал определение окружности.
Начертим окружность с помощью геометрического прибора — циркуля. Построение окружности демонстрационным циркулем на доске:
- отметим точку на плоскости;
- ножку циркуля с остриём совмещаем с отмеченной точкой, а ножку с грифелем вращаем вокруг этой точки.
Получилась геометрическая фигура — окружность.
Так что же такое окружность?
Определение. Окружность — это замкнутая кривая линия, все точки которой находятся на равном расстоянии от данной точки плоскости, называемой центром окружности.
На сколько частей делит окружность плоскость?
Точка О- центр окружности.
ОR — радиус окружности (это отрезок, соединяющий центр окружности с любой её точкой). По-латыни radius- спица колеса.
AB – хорда окружности (это отрезок, соединяющий любые две точки на окружности).
DC – диаметр окружности (это хорда, проходящая через центр окружности). Диаметр- с греческого “ поперечник».
DR– дуга окружности (это часть окружности, ограниченная двумя точками).
Сколько в окружности можно провести радиусов, диаметров?
Часть плоскости внутри окружности и сама окружность образуют круг.
Определение. Круг — это часть плоскости, ограниченная окружностью. Расстояние от любой точки круга до центра круга не превышает расстояния от центра круга до любой точки на окружности.
Чем отличаются друг от друга окружность и круг, и что в них общего?
Как связаны между собой длины радиуса (r) и диаметра (d) одной окружности?
d = 2 * r (d – длина диаметра; r – длина радиуса)
Как связаны между собой длины диаметра и любой хорды?
Диаметр – это наибольшая из хорд окружности!
Окружность – удивительно гармоничная фигура, древние греки считали её самой совершенной, так как окружность – единственная кривая, которая может “ скользить сама по себе”, вращаясь вокруг центра. Основное свойство окружности даёт ответ на вопросы, почему для её вычерчивания используют циркуль и почему колёса делают круглыми, а не квадратными или треугольными. Кстати, о колесе. Это одно из самых великих изобретений человечества. Оказывается, додуматься до колеса было не так просто, как это может показаться. Ведь даже ацтеки, жившие в Мексике, почти до XVI века не знали колеса.
Окружность можно изобразить на клетчатой бумаге без циркуля, то есть от руки. Правда окружность получается определённого размера. (Учитель показывает на клетчатой доске)
Правило изображения такой окружности записывается так 3-1, 1-1, 1-3.
Начертите от руки четверть такой окружности.
Скольким клеткам равен радиус этой окружности? Рассказывают, что великий немецкий художник Альбрехт Дюрер одним движением руки (без правил) мог столь точно нарисовать окружность, что последующая проверка при помощи циркуля (центр указывал художник) не показывала никаких отклонений.
Вы уже знаете, как измерять длину отрезка, находить периметры многоугольников (треугольника, квадрата, прямоугольника). А как измерить длину окружности, если сама окружность – кривая линия, а единица измерения длины – отрезок?
Есть несколько способов измерения длины окружности.
След от круга (один оборот) на прямой.
Учитель на доске чертит прямую, отмечает точку на ней и на границе модели круга. Совмещает их, а затем плавно катит круг по прямой до тех пор, пока отмеченная точка А на окружности не окажется на прямой в точке В. Отрезок АВ тогда будет равен длине окружности.
Леонардо да Винчи: «Движение повозок всегда показывало нам, как спрямлять окружность круга».
а) выполнить чертёж окружности, обведя дно круглого предмета;
б) обернуть дно предмета ниткой (один раз) так, чтобы конец нитки совпал с началом в одной и той же точке окружности;
в) распрямить эту нить до отрезка и по линейке измерить её длину, это и будет длина окружности.
Учитель интересуется результатами измерений у нескольких учеников.
Однако эти способы непосредственного измерения длины окружности малоудобные и дают грубоприблежённые результаты. Поэтому уже с древних времён начали искать более совершенные способы измерения длины окружности. В процессе измерений заметили, что между длиной окружности и длиной её диаметра имеется определённая зависимость.
г) Измерьте диаметр дна предмета (наибольшую из хорд окружности);
д) найдите отношение С:d (с точностью до десятых).
Спросить у нескольких учеников результаты вычислений.
Многие учёные – математики пытались доказать, что это отношение есть число постоянное, не зависящее от размеров окружности. Впервые это удалось сделать древнегреческому математику Архимеду. Он нашёл довольно точное значение этого отношения.
Это отношение стали обозначать греческой буквой 
(читается “пи”) – первая буква греческого слова “периферия” – круг.
С – длина окружности;
d – длина диаметра.
Исторические сведения о числе π:
Архимед, живший в Сиракузах (Сицилия) с 287 г. до 212 г. до н.э., нашёл без измерений, одними лишь рассуждениями значение
На самом деле число π не может быть выражено какой – либо точной дробью. Математик XVI века Лудольф имел терпение вычислить его с 35 десятичными знаками и завещал вырезать это значение π на своём могильном памятнике. В 1946 – 1947 гг. два учёных независимо друг от друга вычислили 808 десятичных знаков числа π. Сейчас же на ЭВМ найдено более миллиарда знаков числа π.
Приближённое значение π с точностью до пяти десятичных знаков можно запомнить по следующей строчке (по числу букв в слове):
π ≈ 3,14159 –“ это я знаю и помню прекрасно”.
Знакомство с формулой длины окружности
Зная то, что С:d = π, чему будет равна длина окружности С?
(Слайд №3) C = πd C = 2πr
Как появилась вторая формула?
Читается: длина окружности равна произведению числа π на её диаметр (или удвоенному произведению числа π на её радиус).
Площадь круга равна произведению числа π на квадрат радиуса.
IV. Решение задач
№1. Найдите длину окружности, радиус которой равен 24 см. Число π округлите до сотых.
Если r = 24 см, то C = 2 π r ≈ 2 3,14 24 = 150,72(см).
Ответ: длина окружности 150,72 см.
№2 (устно): Как найти длину дуги, равной полуокружности?
Задача: Если обтянуть земной шар по экватору проволокой и затем прибавить к её длине 1 метр, то сможет ли между проволокой и землёй проскочить мышь?
Решение: C = 2 πR, С+1 = 2π( R+х) 
Не только мышь, но и крупный кот проскочит в такой промежуток. А казалось бы, что значит 1 м по сравнению с 40 млн. метров земного экватора?
- На какие основные моменты нужно обратить внимание при построении окружности?
- Какие моменты урока был вам наиболее интересны?
- Что нового вы узнали на этом уроке?
Решение кроссворда с картинками (Слайд №3)
Оно сопровождается повторением определений круга, хорды, дуги, радиуса, диаметра, формул длины окружности. И как результат — ключевое слово: «ОКРУЖНОСТЬ» (по горизонтали).
Итог урока: выставление оценок, комментарии по выполнению домашнего задания. Домашнее задание: п. 24, №853, 854. Провести эксперимент по нахождению числа π ещё 2 раза.
К уроку прилагается Презентация «Окружность. Круг».
Видео:Геометрия 7 класс (Урок№16 - Окружность. Задачи на построение.)Скачать
Окружности на клетчатой бумаге
Видео:Построение окружности на клетчатой бумагеСкачать
Задача
а) Постройте окружность, проходящую ровно через 12 узлов клетчатой бумаги.
б) Постройте окружность, проходящую ровно через 6 узлов клетчатой бумаги.
в) Постройте окружность, проходящую ровно через 5 узлов клетчатой бумаги.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать
Подсказка 1
Обратите внимание, что если центр окружности сам является узлом клетчатой бумаги, то количество лежащих на этой окружности узлов кратно четырём. Если же центр окружности находится в середине стороны какой-либо клеточки, то на такой окружности будет расположено чётное число узлов. Это относится и к тем случаям, когда окружность вообще не проходит через узлы клетчатой бумаги, потому что ноль делится как на 2, так и на 4 (и вообще на любое натуральное число).
Видео:Делим окружность НА 5 РАВНЫХ ЧАСТЕЙСкачать
Подсказка 2
Будем считать, что расстояние между соседними узлами клетчатой бумаги равно единице. Тогда на ней можно задать систему координат таким образом, чтобы множество всех узлов в точности совпадало со множеством всех точек, обе координаты которых целочисленны.
а) Воспользуйтесь тем фактом, что если центр окружности радиуса r является началом координат, то количество лежащих на ней узлов клетчатой бумаги есть число целочисленных решений уравнения
б) Если r 2 — нечётное целое число, то в каждой паре вида (x, y), являющейся решением уравнения (1), одно из чисел чётное, а другое — нечётное, причём количество пар, в которых первое число нечётное, равно количеству пар, в которых второе число нечётное.
в) В качестве центра такой окружности можно выбрать точку (1/3, 0).
Видео:Найдите площадь треугольника изображенного на клетчатой бумаге с размером клетки 1х1 см.Скачать
Подсказка 3
Попробуйте изучить окружности, квадраты радиусов которых имеют вид 5 k , 5 k /4 и 5 k /9 соответственно.
Видео:Задача на окружности из ОГЭ-2023!! Разбор за 30 секСкачать
Решение
а) Рассмотрим уравнение
Его решениями являются двенадцать пар чисел вида (±5, 0), (0, ±5), (±3, ±4) и (±4, ±3). Нетрудно убедиться простым перебором, что других целочисленных решений данное уравнение не имеет. Следовательно, на окружности радиуса 5 с центром в начале координат лежит ровно 12 узлов клетчатой бумаги (рис. 1).
б) Пусть центр окружности радиуса 5/2 расположен в точке (1/2, 0). Тогда эта окружность задаётся уравнением
Домножая обе части равенства на 4, можно перейти к такому соотношению:
Если же сделать переобозначения вида a = (2x – 1) и b = 2y, то мы придём к уравнению вида a 2 + b 2 = 25. Оно, как мы знаем из пункта а), имеет в точности 12 целочисленных решений (потому что это решения уравнения (2)), причём ровно в половине из них число a нечётное, а число b — чётное. Значит, уравнение (3) обладает в точности шестью целочисленными решениями. А именно, ему удовлетворяют следующие пары чисел: (3, 0), (–2, 0), (2, ±2) и (–1, ±2). Таким образом, на окружности радиуса 5/2 с центром в точке (1/2, 0) лежит ровно 6 узлов клетчатой бумаги (рис. 2).
в) Внимательный читатель наверняка заметил, что решение пункта б), по существу, вытекало из пункта а). Более того, можно было рассмотреть задачу в более общем виде и доказать такое утверждение: если на окружности радиуса r, центр которой находится в начале координат, лежит 4n узлов клетчатой бумаги и число r 2 — нечётное, то на окружности радиуса r/2 с центром в точке (1/2, 0) расположено 2n узлов. Ниже на примере нашей задачи мы покажем, как подобным методом получить окружность, на которой лежит ровно n узлов.
Для начала рассмотрим окружность с центром в начале координат, радиус которой равен 25. Эта окружность задаётся уравнением
которому, как нетрудно проверить, удовлетворяют двадцать пар целочисленных решений: (±25, 0), (0, ±25), (±7, ±24), (±24, ±7), (±15, ±20) и (±20, ±15). То есть на этой окружности находится ровно 20 узлов клетчатой бумаги.
Теперь рассмотрим окружность радиуса 25/3, центром которой является точка (1/3, 0). Задающее её уравнение имеет вид
что после соответствующих преобразований превращается в соотношение
Как и в пункте б), сделав замену a = (3x – 1), b = 3y, мы получим уравнение a 2 + b 2 = 625, решения которого нам известны. Осталось понять, какие из них нам подходят, а какие — нет. Но это оказывается довольно просто: если c делится на 3, то из каждой четвёрки решений вида (c, d), (c, –d), (d, c), (–d, c) подходит ровно одно. В нашем случае, это (–8, 0), (–2, ±8), (7, ±5). И таким образом, на окружности, которая задана уравнением (5), лежит ровно 5 узлов клетчатой бумаги (рис. 3).
Замечание. Глядя на пять красных точек, изображённых на рис. 3, читатель может подумать, что если последовательно соединить их друг с другом, получится правильный пятиугольник. Однако это не так: у этого пятиугольника между собой равны только три стороны, а две другие немножко меньше. В действительности на клетчатой бумаге расположить правильный пятиугольник нельзя. Как и любой другой правильный многоугольник, за исключением квадрата.
Видео:Деление окружности на 12 равных частейСкачать
Послесловие
Придумав решение самостоятельно или ознакомившись с изложенным выше, читатель, наверное, задастся таким вопросом: правда ли, что какое натуральное число n мы ни возьмём, найдётся такая окружность, на которой лежит ровно n узлов клетчатой бумаги? Оказывается, это действительно так, причём методы построения этих окружностей не слишком отличаются от тех, которые мы уже видели. Вкратце изложим суть дела.
Ключевым моментом решения проблемы является следующая лемма.
Лемма. Уравнение x 2 + y 2 = 5 k имеет ровно 4(k + 1) целочисленных решений для любого целого неотрицательного k.
(На самом деле представленная лемма является частным случаем более общего факта. Именно, пусть r(n) обозначает число всевозможных способов представления натурального n в виде суммы квадратов пары целых чисел. Тогда можно доказать, что r(n) = d1(n) – d3(n), где d1(n) и d3(n) — числа, отвечающие количеству делителей n вида (4k + 1) и (4k + 3) соответственно.)
Для доказательства мы проверяем сначала, что утверждение леммы справедливо при k = 0 и k = 1. В самом деле, уравнение x 2 + y 2 = 1 имеет четыре целочисленных решения: (0, ±1) и (±1, 0). А уравнение x 2 + y 2 = 5 обладает ровно восемью корнями: (±2, ±1) и (±1, ±2).
Потом в дело вступает принцип математической индукции. С его помощью можно доказать, что при всех целых k > 1 уравнение x 2 + y 2 = 5 k имеет ровно восемь таких решений (x, y), что x и y не делятся на 5. Точно так же, как и корни уравнения x 2 + y 2 = 5, эти восемь пар чисел получаются друг из друга перестановкой x и y и изменениями знаков. А вместе с 4(k – 1) парами вида (5a, 5b), где (a, b) — решения уравнения a 2 + b 2 = 5 k –2 , они дают нам в точности 4(k + 1) решений исходного уравнения.
Теперь, вооружившись леммой, мы легко сможем дать ответ на поставленный вопрос. Из соображений симметрии ясно, что если расположить центр окружности в узле клетчатой бумаги (например, в начале координат), то количество лежащих на ней узлов будет делиться на четыре. А из леммы сразу вытекает, что если квадрат радиуса такой окружности равен 5 k , то на этой окружности лежит ровно 4(k + 1) узлов. В частности, на окружности x 2 + y 2 = 25 расположено ровно 12 узлов клетчатой бумаги.
В качестве примера окружности, на которой лежит произвольное наперёд заданное чётное число узлов клетчатой бумаги, мы можем взять окружность, заданную уравнением:
(6)
Чтобы убедиться в том, что она годится (то есть что на ней лежит 2(k + 1) узлов), достаточно повторить рассуждения из решения пункта б) и применить лемму. Если же хочется провести окружность через нечётное число узлов, то можно взять такую:
(7)
Используя лемму и свойства делимости на 3, можно доказать, что на ней лежит ровно (2k + 1) узлов, а выбирая подходящее k, это количество можно сделать любым наперёд заданным нечётным числом.
Окружности, которые задаются уравнениями (6) и (7), называются окружностями Шинцеля, по имени польского математика Анджея Шинцеля (Andrzej Schinzel). Отметим, что для данного натурального числа n эти уравнения задают, вообще говоря, не самую маленькую окружность с n узлами клетчатой бумаги на ней. Например, так происходит с n = 1 (очевидно, можно предъявить окружность сколь угодно маленького радиуса) или с n = 4 (здесь ясно, что существует окружность радиуса 1/√2. Менее тривиальный пример: n = 9. Соответствующая окружность Шинцеля имеет радиус 625/3, однако на окружности с центром (1/3, 0) и радиусом 65/3 также лежит ровно 9 узлов клетчатой бумаги.
Существуют также и менее тривиальные комбинации точек. Так, на рис. 4 изображена окружность с центром в точке (1/5, 2/5) и радиусом 
— на ней лежат четыре узла клетчатой бумаги: (–6, –2), (1, 7), (5, 5) и (2, –6). А на окружности с центром в точке (1/7, 2/7) и радиусом 
находятся пять узлов: , , , и (рис. 5).
Описание множества окружностей, которые проходят ровно через n узлов клетчатой бумаги для заданного натурального числа n, — пока нерешённая задача. Предполагается, что окружность, проходящая более чем через три узла, — достаточно редкое явление, то есть если провести окружность через три случайно выбранных узла клетчатой бумаги, то через четвёртый она пройдёт с малой вероятностью.
С этой задачей также связан вопрос об изображении круга на экране монитора. Будем считать, что экран представляет собой прямоугольный лист клетчатой бумаги, а круг на экране — объединение тех клеточек (пикселей), которые пересекаются со внутренностью круга. Тогда вопрос заключается в том, сколько различных изображений на экране имеет круг данного радиуса. Например, на рис. 6 представлено три различных изображения круга радиуса 4/5 (сторона клеточки, соответственно, равна единице). Полного ответа на этот вопрос пока тоже нет.
При подготовке данной публикации использовалась статья В. Вавилова и А. Устинова Окружности на решетках («Квант» №6, 2006), в которой обсуждаются некоторые свойства целочисленных решеток и расположение окружностей на них.
🎬 Видео
Построение пятиугольника циркулем и линейкойСкачать
7 класс, 23 урок, Примеры задач на построениеСкачать
Построение эвольвенты окружностиСкачать
Деление окружности на равные части с помощью циркуляСкачать
7 класс, 21 урок, ОкружностьСкачать
Построение касательной к окружности.Скачать
Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать
Построить описанную окружность (Задача 1)Скачать
Окружность и задачи на построениеСкачать
Построение окружности по трем точкамСкачать
Построение окружности на ЕГЭСкачать
Найдите площадь заштрихованной фигуры — лайфхаки ЕГЭ #геометрияСкачать
