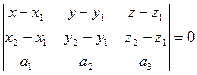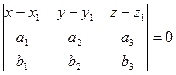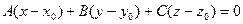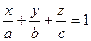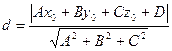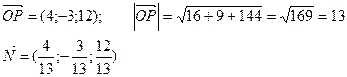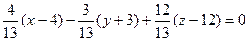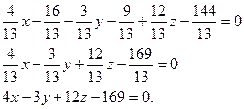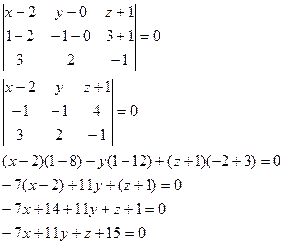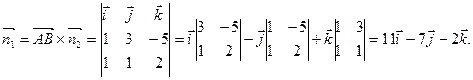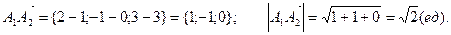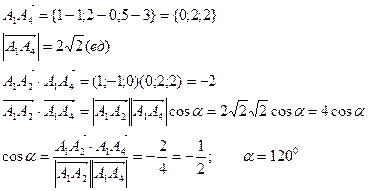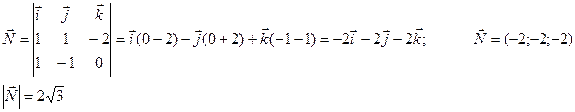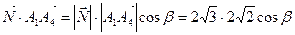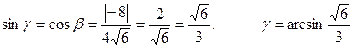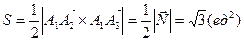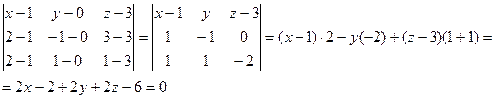Курс школьной геометрии » Вектор

M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны

Обновлено
Координаты и компоненты вектора

Выберем в пространстве ПДСК Oxyz. Обозначим через i, j, k орты положительных направлений осей Ox, Oy, Oz (рис.19). Рассмотрим произвольный вектор а, начало которого лежит в т.О, а конец – в т. А. Проведем через т. А плоскости, перпендикулярные осям Ox, Oy, Oz. Эти плоскости пересекут координатные оси в точках P, Q, R соответственно. Из рис. 17 видно, что a = M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны+ M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны+ M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны. (1)

Векторы M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны, M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны, M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равныколлинеарны соответственно ортам i, j, k, поэтому найдутся числа x, y, z такие, что M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны= xi, M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны= уj, M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны= zk и, следовательно,

а = xi + уj + zk . (2)

Формула (2) называется разложением вектора а по векторамi, j, k .

Векторы i, j, k попарно ортогональны, а их длины равны единице. Тройку i, j, k называют ортонормированным (координатным) базисом или ортобазисом.

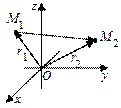M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны
M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны
M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны
M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны

Рис. 19. Рис. 20. Рис.21. Рис.22.

Для каждого вектора а разложение (2) по базису i, j, k единственно, т.е. коэффициенты x, y, z в разложении вектора а по векторам i, j, k определены однозначно. Эти коэффициенты называются координатами вектораа. Они совпадают с координатами

x, y, z т. А – конца вектора а. В этом случае пишется а = <x, y, z >. Эта запись означает, что свободный вектор а однозначно задается упорядоченной тройкой своих координат.

Векторы xi, уj, zk, сумма которых равна вектору а, называется компонентами вектораа.

Из сказанного следует, что два вектораа = <x1, y1, z1 > и b = <x2, y2, z2 > равны тогда и только тогда, когда соответственно равны их координаты, т.е. а = b Û 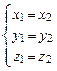M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны.

Радиусом–вектором т.М (x, y, z) называется вектор r = xi + уj + zk, идущий из начала координат О в т.М (рис.20).

Линейные операции над векторами

Пусть имеем два вектора а = <x1, y1, z1 > и b = <x2, y2, z2 >, так что а = x1 i + у1 j + z1 k, b = x2 i + у2 j + z2 k. На основании правила сложения векторов имеем:

попарно складываются.

Далее, lа = lx1 i + lу1 j + lz1 k или lа = lx1, ly1, lz1> — при умножении вектора

на число все его координаты умножаются на это же число.

Пусть а = <x1, y1, z1 > и b = <x2, y2, z2 > – коллинеарные векторы, причем b ¹ 0. Тогда

а = m b, т.е. x1 = m x2 , у1 = m у2 , z1 = m z2 , или M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны. (3)

Обратно, если выполняется (3), то а = m b, т.е. векторы а и b коллинеарны.

Т.о., векторы а и b коллинеарны тогда и только тогда, когда их координаты

Пропорциональны.

Пример. Найти координаты вектора M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны, начало которого находится в т. М1(x1, y1, z1),

Из рис.22 видно, что M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны= r2 – r1 , где r1 и r2 — радиусы-векторы точек М1 и М2

соответственно. Поэтому M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны= < x2 – x1, y2 – y1, z2 – z1> — координаты вектора M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равныравны

разности одноименных координат конечной М2 и начальной М1 точек этого вектора..

M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны
M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны

Проекция вектора на ось

Рассмотрим на оси l ненулевой направленный отрезок АВ (рис.23).

Величиной направленного отрезка АВ на оси l называется число, рав-

ное длине отрезка АВ, взятое со знаком «+», если направление отрезка АВ

совпадает с направление оси l , и со знаком «–», если эти направления Рис.23. Рис.24.

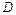
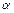
Рассмотрим теперь произвольный вектор M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны, определяемый связанным вектором M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны. Опуская из его начала и конца перпендикуляры на заданную ось l, построим на ней направленный отрезок CD (рис.24).

M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равныПроекцией вектора M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равнына ось l называется величина направленного отрезка CD, построенного указанным выше способом.

Обозначение: prl M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны= CD.

Основные свойства проекций:

  1. Проекция вектора M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равнына какую-либо ось l равна произведению Рис.25.

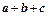
M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равныдлины вектора на косинус угла между осью и этим вектором (рис.25)

prl M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны= | M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны| cosα . Рис.26.

  1. Проекция суммы векторов на какую-либо ось l равна сумме проекций

векторов на эту же ось. Например, prl (a + b + c) = prl a + prl b + prl c (рис.26).

Пусть заданы точки М1(x1, y1, z1), M2(x2, y2, z2) и вектор .

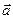
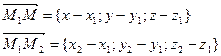
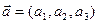
Составим уравнение плоскости, проходящей через данные точки М1 и М2 и произвольную точку М(х, у, z) параллельно вектору M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны.

Векторы M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равныи вектор M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равныдолжны быть компланарны, т.е.

( M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны) = 0

M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равныУравнение плоскости:

M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны

Уравнение плоскости по одной точке и двум векторам,

коллинеарным плоскости.

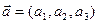
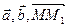
Пусть заданы два вектора M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равныи M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны, коллинеарные плоскости. Тогда для произвольной точки М(х, у, z), принадлежащей плоскости, векторы M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равныдолжны быть компланарны.

M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равныM x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны

Уравнение плоскости по точке и вектору нормали.

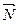
M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равныТеорема. Если в пространстве задана точка М0(х0, у0, z0), то уравнение плоскости, проходящей через точку М0 перпендикулярно вектору нормали M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны(A, B, C) имеет вид:

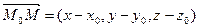
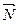
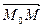
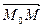
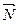
Доказательство. Для произвольной точки М(х, у, z), принадлежащей плоскости, составим вектор M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны. Т.к. вектор M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны— вектор нормали, то он перпендикулярен плоскости, а, следовательно, перпендикулярен и вектору M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны. Тогда скалярное произведение

M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны× M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны= 0

Таким образом, получаем уравнение плоскости

M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны

Уравнение плоскости в отрезках.

Если в общем уравнении Ах + Ву + Сz + D = 0 поделить обе части на (-D)

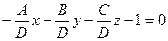
M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны,

заменив 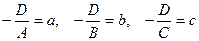M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны, получим уравнение плоскости в отрезках:

M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны

M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны

Числа a, b, c являются точками пересечения плоскости соответственно с осями х, у, z.

Уравнение плоскости в векторной форме.

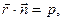
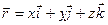
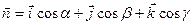
M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равныгде

M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны— радиус- вектор текущей точки М(х, у, z),

M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны— единичный вектор, имеющий направление, перпендикуляра, опущенного на плоскость из начала координат.

a, b и g — углы, образованные этим вектором с осями х, у, z.

p – длина этого перпендикуляра.

В координатах это уравнение имеет вид:

M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны

xcosa + ycosb + zcosg — p = 0.

Расстояние от точки до плоскости.

M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равныРасстояние от произвольной точки М0(х0, у0, z0) до плоскости Ах+Ву+Сz+D=0 равно:

M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны

Пример. Найти уравнение плоскости, зная, что точка Р(4; -3; 12) – основание перпендикуляра, опущенного из начала координат на эту плоскость.

M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны

Таким образом, A = 4/13; B = -3/13; C = 12/13, воспользуемся формулой:

M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны

M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны

Пример. Найти уравнение плоскости, проходящей через две точки P(2; 0; -1) и

Q(1; -1; 3) перпендикулярно плоскости 3х + 2у – z + 5 = 0.

Вектор нормали к плоскости 3х + 2у – z + 5 = 0 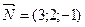M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равныпараллелен искомой плоскости.

M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны

Пример. Найти уравнение плоскости, проходящей через точки А(2, -1, 4) и

В(3, 2, -1) перпендикулярно плоскости х + у + 2z – 3 = 0.

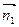
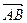
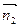
Искомое уравнение плоскости имеет вид: Ax + By + Cz + D = 0, вектор нормали к этой плоскости M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны(A, B, C). Вектор M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны(1, 3, -5) принадлежит плоскости. Заданная нам плоскость, перпендикулярная искомой имеет вектор нормали M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны(1, 1, 2). Т.к. точки А и В принадлежат обеим плоскостям, а плоскости взаимно перпендикулярны, то

M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны

Таким образом, вектор нормали 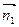M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны(11, -7, -2). Т.к. точка А принадлежит искомой плоскости, то ее координаты должны удовлетворять уравнению этой плоскости, т.е. 11×2 + 7×1 — 2×4 + D = 0; D = -21.

Итого, получаем уравнение плоскости: 11x — 7y – 2z – 21 = 0.

Пример. Найти уравнение плоскости, зная, что точка Р(4, -3, 12) – основание перпендикуляра, опущенного из начала координат на эту плоскость.

Находим координаты вектора нормали 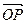M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны= (4, -3, 12). Искомое уравнение плоскости имеет вид: 4x – 3y + 12z + D = 0. Для нахождения коэффициента D подставим в уравнение координаты точки Р:

16 + 9 + 144 + D = 0

Итого, получаем искомое уравнение: 4x – 3y + 12z – 169 = 0

Пример. Даны координаты вершин пирамиды А1(1; 0; 3), A2(2; -1; 3), A3(2; 1; 1),

M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны

M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны

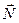
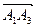
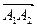
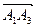
Сначала найдем вектор нормали к грани А1А2А3 M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равныкак векторное произведение векторов M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равныи M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны.

M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны= (2-1; 1-0; 1-3) = (1; 1; -2);

M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны

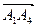
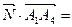
Найдем угол между вектором нормали и вектором M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны.

M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны

M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны-4 – 4 = -8.

Искомый угол g между вектором и плоскостью будет равен g = 90 0 — b.

M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны

M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны

5) Найти объем пирамиды.

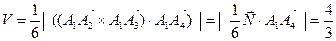
M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны(ед 3 ).

Воспользуемся формулой уравнения плоскости, проходящей через три точки.

M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны

2x + 2y + 2z – 8 = 0

При использовании компьютерной версии “Курса высшей математики” можно запустить программу, которая решит рассмотренный выше пример для любых координат вершин пирамиды.

Для запуска программы дважды щелкните на значке:

M x1 y1 z1 k x2 y2 z2 тогда координаты вектора km равны

В открывшемся окне программы введите координаты вершин пирамиды и, нажимите Enter. Таким образом, поочередно могут быть получены все пункты решения.

Примечание: Для запуска программы необходимо чтобы на компьютере была установлена программа Maple (Ó Waterloo Maple Inc.) любой версии, начиная с MapleV Release 4.

Геометрия. 11 класс

Скалярное произведение векторов
Скалярное произведение векторов
Необходимо запомнить

Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Запишем формулу: $overrightarrowcdotoverrightarrow = |overrightarrow|cdot|overrightarrow|cosalpha$

Косинус угла между векторами пространства

$overline(nu_;nu_;nu_), overline(omega_;omega_;omega_),$ заданными в ортонормированном базисе

1) $overrightarrow<a^> geq 0,$ причем $overrightarrow<a^> > 0$ при $overrightarrow neq overrightarrow.$

Формула нахождения угла между двумя прямыми:

Формула нахождения угла между прямой и плоскостью:

Скалярное произведение векторов

Докажем основные свойства скалярного произведения.

Докажем первое свойство

$overrightarrowgeq0$, причем $overrightarrowgt 0$ при $overrightarrowneoverrightarrow$

Доказательство:эти свойства очень легко обосновать, если отталкиваться от определения скалярного произведения в координатной форме и от свойств операций сложения и умножения действительных чисел.

Докажем второе свойство

Доказательство: По определению скалярного

того, воспользуемся свойством переместительности

Докажем третье свойство

Докажем четвертое свойство

координат и рассмотрим произвольные

формулой скалярного произведения в координатах

Поделиться или сохранить к себе: