Любой четырехугольник можно вписать окружность верно

Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.

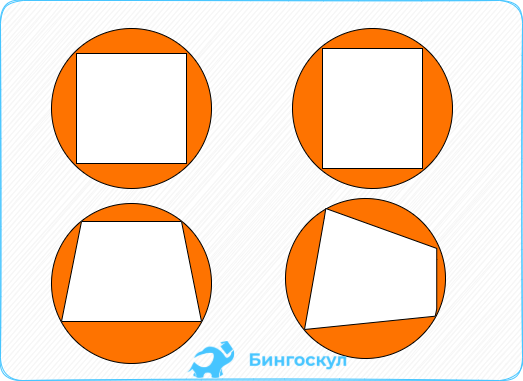
Окружность, точно можно вписать в такие геометрические фигуры, как:

• Треугольник
• Выпуклый, правильный многоугольник
• Квадрат
• Равнобедренная трапеция
• Ромб

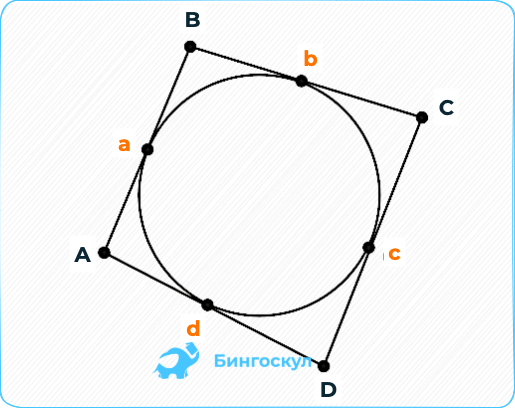
В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.

Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.

Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.

Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.

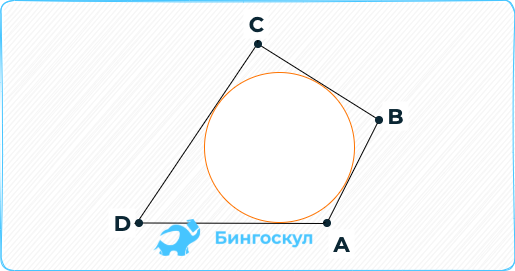
Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.

Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.

Свойства вписанной окружности

В треугольник

1. В любой треугольник может быть вписана окружность, причем только один раз.
2. Центр вписанной окружности — точка пересечения биссектрис треугольника.
3. Вписанная окружность касается всех сторон треугольника.
4. Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:

[ S = frac(a+b+c) cdot r = pr ]

p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.

Примеры вписанной окружности

• Треугольник
  
• Четырехугольник
  
• Многоугольник
  

Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.

Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.

Верные и неверные утверждения

1. Радиус вписанной окружности в треугольник и радиус вписанной
   в четырехугольник вычисляется по одной и той же формуле. Верное утверждение.
2. Любой параллелограмм можно вписать в окружность. Неверное утверждение.
3. В любой четырехугольник можно вписать окружность. Неверное утверждение.
4. В любой ромб можно вписать окружность. Верное утверждение.
5. Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
6. Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
7. Угол вписанный в окружность равен соответствующему центральному
   углу опирающемуся на ту же дугу. Неверное утверждение.
8. Радиус вписанной окружности в прямоугольный треугольник равен
   половине разности суммы катетов и гипотенузы. Верное утверждение.
9. Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
10. Вписанная окружность в треугольник имеет в общем
    три общие точки со всеми сторонами треугольника. Верное утверждение.

Окружность вписанная в угол

Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.

Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.

К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.

Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.

Видео:В любой четырёхугольник можно вписать окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Любой четырехугольник можно вписать окружность верно

Какие из данных утверждений верны? Запишите их номера.

1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90° , то эти две прямые параллельны.

2) В любой четырёхугольник можно вписать окружность.

3) Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника.

Проверим каждое из утверждений.

1) «Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90° , то эти две прямые параллельны» — верно, по признаку параллельности прямых.

2) «В любой четырёхугольник можно вписать окружность» — неверно, поскольку в выпуклый четырёхугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны.

3) «Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника» — верно, по свойству треугольника.

Видео:Если в четырёхугольник можно вписать окружностьСкачать

Любой четырехугольник можно вписать окружность верно или нет ответ

Видео:№700. Докажите, что в любой ромб можно вписать окружность.Скачать

Можно ли вписать четырёхугольник в окружность? Когда можно вписать?

Содержание:

Почти в любой четырехугольник можно вписать окружность. Трапеция, прямоугольник и квадрат для этого подходят всегда, тогда как сложные геометрические фигуры с четырьмя углами вписываются в круг избирательно. Рассмотрим условия, при которых 4-угольник может касаться точек на окружности всеми вершинами.

Видео:Окружность, вписанная в четырехугольникСкачать

Вписанный

Вписанной называется фигура, вершины которой располагаются на окружности. Все треугольники и правильные 4-угольники, вроде квадрата и прямоугольника, размещаются внутри круга, причём их вершины совмещаются с точками на окружности. Вокруг неправильной фигуры с четырьмя углами не всегда можно описать круг. Разбираемся, какие условия нужно выполнить для решения проблемы.

У квадрата и прямоугольника все углы прямые – равны 90°, но это не ключ к разгадке. Случай с параллелограммом тому подтверждение. Чем примечательны прямоугольные 4-угольники? Может дело в сумме углов?

Трапеция в круг вписывается, но только равнобедренная. Одно из её свойств – сумма внутренних углов равна 360°, а соседних – 180°. Получается, что четырехугольник можно вписать в окружность, если сумма противоположных углов равняется 180°. Проверим на практике.

Помните: правило применимо только для выпуклых фигур, расположенных по одну сторону от проходящих через все стороны прямых.

Выпуклый дельтоид вписывается в круг, когда имеет пару прямых углов – называется прямоугольным.

Задача

Известны величины двух соседних углов вписанного четырёхугольника: 65° и 83°. Вычислить размеры сразу большего, затем – меньшего из оставшихся.

Известно, что сумма противоположных углов указанной геометрической фигуры равняется 180°. Отнимем от значения сначала большую цифру, затем – меньшую, чтобы выполнить условия задачи – найти неизвестные значения в указанном порядке.

180 – 65 = 115° – больший угол, 180 – 83 = 97° – меньший.

Видео:Свойство четырехугольника, в который можно вписать окружностьСкачать

В какой четырехугольник можно вписать окружность

Описанным называют 4-угольник, стороны которого касаются круга. Существует теорема, показывающая, когда в четырехугольник можно вписать окружность: сумма его противоположных сторон должна быть одинаковой: AB + CD = BC + AD. В случае с прямоугольником условие не выполняется.

Правило работает для дельтоида, квадрата и даже неправильного выпуклого 4-угольника, подпадающего под теорему.

В параллелограмм вписывается круг в случае, если он является ромбом.

Задача

Стороны описанной фигуры относятся как 1:2:3. Найти длину четвёртой, если периметр равняется 32 см.

Составим уравнение. Зная, что суммы противоположных сторон 4-угольника равны:

Периметр равняется суме сторон: P = AB + ВС + AD + BC либо x + 2x + 2x + 3x = 32.

Видео:В любой треугольник можно вписать окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Любой четырехугольник можно вписать окружность верно или нет ответ

Какие из данных утверждений верны? Запишите их номера.

1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90° , то эти две прямые параллельны.

2) В любой четырёхугольник можно вписать окружность.

3) Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника.

Проверим каждое из утверждений.

1) «Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90° , то эти две прямые параллельны» — верно, по признаку параллельности прямых.

2) «В любой четырёхугольник можно вписать окружность» — неверно, поскольку в выпуклый четырёхугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны.

3) «Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника» — верно, по свойству треугольника.

Видео:В любой ромб можно вписать окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Любой четырехугольник можно вписать окружность верно или нет ответ

Задание 19. Какое из следующих утверждений верно?

1) Сумма углов выпуклого четырёхугольника равна 360 градусам.

2) Средняя линия трапеции равна сумме её оснований.

3) Любой параллелограмм можно вписать в окружность.

1) Да, сумма всех углов выпуклого четырёхугольника равна 360 градусам.

2) Нет, средняя линия трапеции равна полусумме её оснований.

3) Нет, не любой параллелограмм можно вписать в окружность.

• Вариант 1
• Вариант 1. Задания по ОГЭ 2022. Математика. И.В. Ященко. 36 вариантов
• Решения заданий по номерам
  • 1-5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
• Вариант 2
• Вариант 2. Задания по ОГЭ 2022. Математика. И.В. Ященко. 36 вариантов
• Решения заданий по номерам
  • 1-5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
• Вариант 3
• Вариант 3. Задания по ОГЭ 2022. Математика. И.В. Ященко. 36 вариантов
• Решения заданий по номерам
  • 1-5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
• Вариант 4
• Вариант 4. Задания по ОГЭ 2022. Математика. И.В. Ященко. 36 вариантов
• Решения заданий по номерам
  • 1-5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
• Вариант 5
• Вариант 5. Задания по ОГЭ 2022. Математика. И.В. Ященко. 36 вариантов
• Решения заданий по номерам
  • 1-5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
• Вариант 6
• Вариант 6. Задания по ОГЭ 2022. Математика. И.В. Ященко. 36 вариантов
• Решения заданий по номерам
  • 1-5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
• Вариант 7
• Вариант 7. Задания по ОГЭ 2022. Математика. И.В. Ященко. 36 вариантов
• Решения заданий по номерам
  • 1-5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
• Вариант 8
• Вариант 8. Задания по ОГЭ 2022. Математика. И.В. Ященко. 36 вариантов
• Решения заданий по номерам
  • 1-5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
• Вариант 9
• Вариант 9. Задания по ОГЭ 2022. Математика. И.В. Ященко. 36 вариантов
• Решения заданий по номерам
• Задания 1-5 полностью совпадают с Вариант 1. Задания по ОГЭ 2021. Математика. И.В. Ященко. 36 вариантов
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
• Вариант 10
• Вариант 10. Задания по ОГЭ 2022. Математика. И.В. Ященко. 36 вариантов
• Решения заданий по номерам
• Задания 1-5 полностью совпадают с Вариант 2. Задания по ОГЭ 2021. Математика. И.В. Ященко. 36 вариантов
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25

  Внимание! Нумерация заданий в сборнике 2021 отличается от сборника 2020

• 
• Вариант 11
• Задания совпадают с Вариант 1. Задания по ОГЭ 2021. Математика. И.В. Ященко. 36 вариантов
• Кроме заданий:
  • 1-5
  • 25
• Вариант 12
• Задания совпадают с Вариант 2. Задания по ОГЭ 2021. Математика. И.В. Ященко. 36 вариантов
• Кроме заданий:
  • 1-5
  • 25
• Вариант 13
• Задания 1-5 совпадают с Вариант 19. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
• Задания совпадают с Вариант 3. Задания по ОГЭ 2021. Математика. И.В. Ященко. 36 вариантов
• Кроме заданий:
  • 23
• Вариант 14
• Задания 1-5 совпадают с Вариант 20. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
• Задания совпадают с Вариант 4. Задания по ОГЭ 2021. Математика. И.В. Ященко. 36 вариантов
• Кроме заданий:
  • 23
• Вариант 15
• Задания 1-5 совпадают с Вариант 13. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
• Задания совпадают с Вариант 5. Задания по ОГЭ 2021. Математика. И.В. Ященко. 36 вариантов
• Кроме заданий:
  • 25
• Вариант 16
• Задания 1-5 совпадают с Вариант 14. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
• Задания совпадают с Вариант 6. Задания по ОГЭ 2021. Математика. И.В. Ященко. 36 вариантов
• Кроме заданий:
  • 25
• Вариант 17
• Задания 1-5 совпадают с Вариант 5. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
• Задания совпадают с Вариант 1. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
• Кроме заданий:
  • 14
• Вариант 18
• Задания 1-5 совпадают с Вариант 6. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
• Задания совпадают с Вариант 2. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
• Кроме заданий:
  • 14
• Вариант 19
• Задания совпадают с Вариант 3. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
• Кроме заданий:
  • 1-5
  • 8
  • 14
  • 24
• Вариант 20
• Задания совпадают с Вариант 4. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
• Кроме заданий:
  • 1-5
  • 8
  • 14
• Вариант 21
• Задания совпадают с Вариант 5. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
• Кроме заданий:
  • 1-5
  • 8
  • 14
  • 21
• Вариант 22
• Задания совпадают с Вариант 6. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
• Кроме заданий:
  • 1-5
  • 8
  • 14
  • 21
  • 22
  • 23
• Вариант 23
• Задания совпадают с Вариант 7. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
• Кроме заданий:
  • 1
  • 8
  • 14
  • 25
• Вариант 24
• Задания совпадают с Вариант 8. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
• Кроме заданий:
  • 1
  • 8
  • 14
  • 25
• Вариант 25
• Задания совпадают с Вариант 9. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
• Кроме заданий:
  • 1
  • 14
• Вариант 26
• Задания совпадают с Вариант 10. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
• Кроме заданий:
  • 1
  • 14
• Вариант 27
• Задания 1-5 совпадают с Вариант 17. Задания по ОГЭ 2021. Математика. И.В. Ященко. 36 вариантов
• Задания совпадают с Вариант 11. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
• Кроме заданий:
  • 14
  • 25
• Вариант 28
• Задания 1-5 совпадают с Вариант 18. Задания по ОГЭ 2021. Математика. И.В. Ященко. 36 вариантов
• Задания совпадают с Вариант 12. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
• Кроме заданий:
  • 14
  • 24
  • 25
• Вариант 29
• Задания совпадают с Вариант 13. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
• Кроме заданий:
  • 1-5
  • 8
  • 14
  • 25
• Вариант 30
• Задания совпадают с Вариант 14. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
• Кроме заданий:
  • 1
  • 8
  • 25
• Вариант 31
• Задания 1-5 совпадают с Вариант 29. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
• Задания совпадают с Вариант 15. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
• Кроме заданий:
  • 8
  • 14
• Вариант 32
• Задания 1-5 совпадают с Вариант 30. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
• Задания совпадают с Вариант 16. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
• Кроме заданий:
  • 8
  • 14
• Вариант 33
• Задания совпадают с Вариант 17. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
• Кроме заданий:
  • 1-5
  • 14
• Вариант 34
• Задания совпадают с Вариант 18. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
• Кроме заданий:
  • 1-5
  • 14
• Вариант 35
• Задания 1-5 совпадают с Вариант 15. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
• Задания совпадают с Вариант 19. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
• Кроме заданий:
  • 14
• Вариант 36
• Задания 1-5 совпадают с Вариант 16. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
• Задания совпадают с Вариант 20. Задания по ОГЭ 2020. Математика. И.В. Ященко. 36 вариантов
• Кроме заданий:
  • 14

🎦 Видео

№8. Верно ли утверждение: а) если две точки окружности лежат в плоскостиСкачать

Любой прямоугольник можно вписать в окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Вписанный в окружность четырёхугольник.Скачать

Урок 1. Вписанная окружность в четырехугольник. Теория+ практикаСкачать

Свойство четырехугольника, в который можно вписать окружностьСкачать

ЧЕТЫРЕХУГОЛЬНИК и ОКРУЖНОСТЬ | ЕГЭ Математика | @matematikajСкачать

Любой квадрат можно вписать в окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

8 класс, 38 урок, Вписанная окружностьСкачать

Окружность, описанная около четырёхугольникаСкачать

найти сторону четырехугольника, в который вписана окружностьСкачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

№696. Докажите, что если в параллелограмм можно вписать окружность, то этот параллелограмм — ромб.Скачать

В любой прямоугольник можно вписать окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать