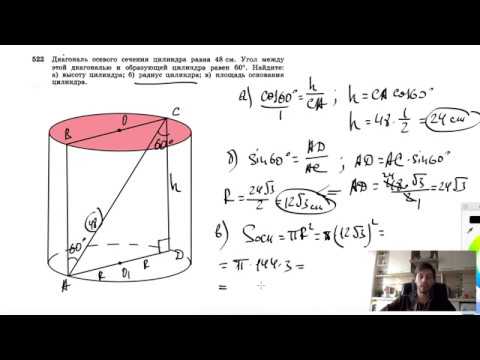
Ответь на вопросы. Назови элементы цилиндра (боковая поверхность, основание, ось, радиус, образующая, высота ). 2.Назови вид осевого сечения цилиндра. 3. Может ли сечение цилиндра быть: -прямоугольником (да) -квадратом (да) -трапецией?(нет). 4.Какие из данных утверждений верны: -любое сечение цилиндра плоскостью, перпендикулярной основанию есть окружность, равная окружности основания; (неверно) любое сечение цилиндра плоскостью есть окружность, равная окружности основания; (неверно) -плоскость, перпендикулярная оси цилиндра, пересекает его по кругу, равному основанию цилиндра; (верно) -сечением цилиндра могут быть круг, прямоугольник, эллипс.(верно).
Слайд 47 из презентации «Цилиндр»
Размеры: 720 х 540 пикселей, формат: .jpg. Чтобы бесплатно скачать слайд для использования на уроке, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «Цилиндр.ppt» можно в zip-архиве размером 6191 КБ.
Видео:№531. Высота цилиндра равна 10 дм. Площадь сечения цилиндра плоскостью, параллельнойСкачать

Цилиндр
«Цилиндром называется тело» — Задача № 2. Высота цилиндра 8 м, радиус основания 5 м. Цилиндр пересечен плоскостью так, что в сечении получился квадрат. Задача № 1. В цилиндр вписана правильная шестиугольная призма. Решение: Цилиндры. Проект «Математика в профессии «Повар, кондитер». Цилиндр, осевое сечение, которого-квадрат называется равносторонним.
«Цилиндр конус шар» — Оглавление. Найти объём и площадь поверхности шара. Определение конуса. Объёмы и поверхности тел вращения. Сечение шара плоскостью есть круг. Объема сегмента. Определение цилиндра. Завершить работу. Сечения шара. Определение шара. Тела вращения. Объём шарового сектора. Шаровой сектор . Объём шарового сегмента.
«Цилиндр» — Цилиндрическая поверхность. Объем цилиндра. Радиус цилиндра. Основания цилиндра. Цилиндр. Образующие цилиндра параллельны друг другу. Ось цилиндра.
«Понятие цилиндра» — Ножницы. Цилиндры вокруг нас. Не правда ли захватывает дух. Решение задач. Прямоугольник. Откуда и как появился цилиндр. Чудо. Сечения цилиндра. Что такое цилиндр. Счастье было потеряно навсегда. Объем цилиндра. Тело вращения. Кружочки. В честь шляпы. Добрые ножницы. Вписанный и описанный цилиндр. Два милых кружочка.
«Поверхность цилиндра» — Образующие. «Понятие цилиндра». A. Shevchenko R. Trushenkov. Осевое сечение. Стороны AB и СD — представляют собой 2 края разреза боковой поверхности цилиндра. Ось цилиндра. Основания цилиндра. Sбок = 2¶r sцил = 2¶r(r+h). «Общие формулы». Algebra & Geometria Entertainment.
«Задачи на цилиндр» — Конус. Примеры цилиндра. 1. Центры оснований цилиндра. 1. Сечением является квадрат ABCD, значит AB=AD=OO1=8дм. Площади оснований. Наклонными. Геометрическое тело, Проверь себя. Дано: цилиндр, ABCD — прямоугольник, осевое сечение. 5. Найдем площадь сечения. 4. Ось цилиндра. Какой цилиндр называется прямым?
Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Урок геометрии в 11-м классе по теме «Понятие цилиндра. Площадь поверхности цилиндра»
Разделы: Математика
Тип урока: урок изучения нового материала.
Цели урока:
- Ввести понятия цилиндрической поверхности цилиндра и его элементов (боковая поверхность, основания, образующие, ось, высота, радиус).
- Рассмотреть сечения цилиндра плоскостью.
- Вывести формулы для вычисления площадей боковой и полной поверхностей цилиндра.
- Закрепить понятия с помощью выполнения заданий.
- Способствовать развитию у учащихся умения самостоятельно формулировать цели и задачи.
- Формировать понимание взаимосвязи между предметами математика и информатика.
- Развивать пространственное воображение.
- Воспитывать внимание, аккуратность, бережное отношение к техническим средствам.
- Способствовать осознанию ценности коллективной мыслительной деятельности.
- Формировать представление о математике, как о части общечеловеческой культуры.
Оборудование и материалы:
- ПК.
- Мультимедийный проектор.
- Интерактивная маркерная доска.
- Презентация “Цилиндр”. (Приложение 1)
- Бланки с рисунками цилиндров и самостоятельной работой. (Приложение 2)
Ход урока
Учитель: Тема нашего урока «Понятие цилиндра. Площадь поверхности цилиндра» или, кратко, “Цилиндр”. С данным геометрическим телом вы знакомы давно. Какие предметы из окружающей среды напоминают вам цилиндр?
Учитель: Используя алгоритм, по которому мы изучали многогранники в 10-м классе, подумайте и скажите, что мы можем узнать о цилиндре? (Из каких элементов состоит цилиндр; познакомиться с сечениями цилиндра; нахождение площади поверхности цилиндра).
Учитель: Сейчас вы самостоятельно поставили цель нашего урока и составили план работы. Сегодня мы будем работать по следующему плану (Слайд 2). На партах у вас раздаточный материал (лист с чертежами цилиндров). Он будет необходим при работе на уроке. Учащиеся класса будут объяснять материал используя свои презентации. Слово предоставляется Ученику №1.
Пусть L — произвольная линия, лежащая в плоскости α и m – прямая, пересекающая эту плоскость.
Цилиндрической поверхностью называется поверхность, образованная движением прямой АВ, которая непрерывно перемещается параллельно m вдоль линии L. Движущаяся прямая называется образующей, а линия L — направляющей.
Цилиндрическая поверхность называется замкнутой, если линия L- замкнутая, и незамкнутой, если линия L – незамкнутая.
Цилиндрическим телом или цилиндром называется тело, ограничение замкнутой цилиндрической поверхностью и двумя пересекающими её параллельными плоскостями:
— часть цилиндрической поверхности, ограничивающей цилиндр — боковая поверхность;
— части секущих параллельных плоскостей, выделяемые цилиндрической поверхностью — его основания;
— часть образующей цилиндрической поверхности — образующая цилиндра
— если в основании цилиндра круг — цилиндр круговой.
Другие виды цилиндров.
Учитель: Ученик № 2 расскажет нам о прямом круговом цилиндре.
Прямым круговым цилиндром называют цилиндр, у которого в основании лежат круги, а образующая перпендикулярна основаниям. В дальнейшем прямой круговой цилиндр будем называть просто “цилиндр”. Его элементы: ось, радиус, высота, образующая, основания, боковая поверхность.
Нанесите на заготовленный чертеж данные элементы и подумайте над определениями этих понятий.
Проверим, насколько верно вы дали определения.
Цилиндр можно рассматривать как тело, полученное вращением прямоугольника вокруг одной из его сторон.
Учитель: Следующий пункт плана – сечения цилиндра. На партах у вас модели цилиндров. Рассмотрите и подумайте, как можно провести сечения, и какие геометрические фигуры получатся в результате. (Прямоугольник, овал или эллипс, круг.)
Посмотрим, как они выглядят и воспроизведем на заготовках чертежей. Слово предоставляется Ученику № 3.
Слайд 10, 11, 12, 13.
Учитель: Площади боковой и полной поверхностей цилиндра. Как они вычисляются, нам расскажет Ученик № 4.
Учащийся объясняет п.54 учебника “Геометрия 10-11” (авторы: Л.С. Атанасян и др.). Полезно показать, как получается развертка на заранее приготовленной модели.
Удобно при решении задач применять следующие факты (дать понятие подобных цилиндров и отношение из полных и боковых поверхностей).
После вывода и записи формулы учащийся предлагает на 2 варианта решить задачу (Слайд 16, 17), после чего, осуществляется взаимопроверка (работа в паре).
Учитель: О цилиндрах вокруг нас нам расскажет Ученик № 5, который показывает свою презентацию.
Учитель: Переходим к проверочной работе (Слайд 39). Тексты проверочной работы лежат у каждого на парте.
Проверочная работа
Ответьте на вопросы:
- Перечислите элементы цилиндра.
- Назовите вид осевого сечения цилиндра.
- Может ли сечение цилиндра быть:
- Какие из данных утверждений верны:
— любое сечение цилиндра плоскостью, перпендикулярной основанию есть окружность, равная окружности основания;
— любое сечение цилиндра плоскостью есть окружность, равная окружности основания;
— плоскость, перпендикулярная оси цилиндра, пересекает его по кругу, равному основанию цилиндра;
— сечением цилиндра могут быть круг, прямоугольник, эллипс.
Итог
Учитель подводит итоги урока, благодарит помощников, анализирует уровень усвоения теоретического материала, задает задание на дом (Слайд 40).
Видео:Сечение цилиндра плоскостьюСкачать

зачет по математике (темы:многогранники, тела вращения, производная)
методическая разработка по алгебре (11 класс) на тему
Контрольно – оценочный материал для тестирования по дисциплине «Математика» по окончании 3 семестра 2015 – 2016 учебного года в группах СПО по профессиям: «Сварщик (электросварочные и газосварочные работы)», «Автомеханик»
Видео:11 класс, 27 урок, Сечения цилиндрической поверхностиСкачать

Скачать:
| Вложение | Размер |
|---|---|
| zachet_po_matematike.docx | 112.94 КБ |
Видео:РТ_ПБ_61.1) Построить проекции линии пересечения цилиндра плоскостью частного положения.Скачать

Предварительный просмотр:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ САРАТОВСКОЙ ОБЛАСТИ
ГАПОУ СО «САРАТОВСКИЙ ТЕХНИКУМ ПРОМЫШЛЕННЫХ ТЕХНОЛОГИЙ И АВТОМОБИЛЬНОГО СЕРВИСА»
Рассмотрено и одобрено на заседании
Протокол № ________от __________
Зам директора филиала по УПР
«_____» _______________________20 ___г.
Контрольно – оценочный материал
для ДФК (тестирование)
по дисциплине «Математика»
по окончании 3 семестра 2015 – 2016 учебного года
в группе СПО № 225
профессия: «Сварщик (электросварочные и газосварочные работы)»
Преподаватель: Усынкина О. В.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ САРАТОВСКОЙ ОБЛАСТИ
ГАПОУ СО «САРАТОВСКИЙ ТЕХНИКУМ ПРОМЫШЛЕННЫХ ТЕХНОЛОГИЙ И АВТОМОБИЛЬНОГО СЕРВИСА»
Рассмотрено и одобрено на заседании
Протокол № ________от __________
Зам директора филиала по УПР
«_____» _______________________20 ___г.
Контрольно – оценочный материал
для ДФК (тестирование)
по дисциплине «Математика»
по окончании 3 семестра 2015 – 2016 учебного года
в группе СПО № 222
Преподаватель: Усынкина О. В.
- Многогранник – это тело, поверхность которого состоит из:
- параллелограммов
- многоугольников и треугольников
- многоугольников
- многоугольников и параллелограммов
- Если боковые ребра призмы перпендикулярны к основаниям, то призма называется
- правильной
- прямой
- наклонной
- перпендикулярной
- Диагональ многогранника – это отрезок, соединяющий
- любые две вершины многогранника
- две вершины, не принадлежащие одной грани
- две вершины, принадлежащие одной грани
- две вершины, одного основания
- Площадь боковой поверхности прямой призмы равна
- произведению периметра основания на длину бокового ребра призмы
- произведению периметра основания на апофему
- произведению длины ребра основания на высоту призмы
- произведению длин ребер основания на высоту призмы
- Количество ребер шестиугольной призмы
- 18
- 6
- 24
- 12
- Наименьшее число граней призмы
- 3
- 4
- 5
- 6
- Параллелепипед – это тело, поверхность которого состоит из:
- параллелограммов
- четырех параллелограммов
- поверхность, составленная из параллелограмма и четырех треугольников
- поверхность, составленная из шести параллелограммов
- Свойство пирамиды: если боковые ребра пирамиды равнонаклонены к основанию, то они равны, а вершина пирамиды проектируется
- в центр окружности, описанной около основания
- в центр окружности, вписанной в основание
- в центр основания
- в одну из вершин основания
- Апофема – это
- высота пирамиды
- высота боковой грани пирамиды;
- высота боковой грани правильной пирамиды
- высота основания пирамиды
- Площадь полной поверхности пирамиды равна
- сумме площади ее боковой поверхности и площади основания
- сумме квадратов трех ее измерений
- сумме площадей двух ее граней
- сумме площади ее боковой поверхности и двух площадей оснований
- Постройте правильную треугольную пирамиду и укажите ее основные элементы.
- 8. Ребро куба объемом 27 куб. см.
- Не является правильным многогранником
а) правильный тетраэдр;
б) правильный додекаэдр;
в) правильная пирамида;
г) правильный октаэдр.
Сфера и плоскость имеют одну общую точку, если…
А. расстояние от центра сфера до плоскости меньше радиуса сферы;
Б. расстояние от центра сфера до плоскости равно радиусу сферы;
В. расстояние от центра сфера до плоскости больше радиуса сферы.
- Установите, какое утверждение неверно.
А. любое сечение цилиндра плоскостью, перпендикулярной оси, есть окружность, равная окружности основания;
Б. любое сечение цилиндра плоскостью есть окружность, равная окружности основания;
В. сечением цилиндра плоскостью могут быть круг, прямоугольник, эллипс.
- Укажите фигуры, в результате вращения которых, наиболее вероятно может получиться конус:
А. остроугольный треугольник; В. прямоугольный треугольник;
Б. равносторонний треугольник; Г. равнобедренная трапеция.
- Укажите плоскую фигуру, с помощью которой получилась фигура вращения.
А. Б. В.
- 2) 3) 4) 5) 6)
- Определите верность утверждений.






![[Начертательная геометрия] Сечение цилиндра плоскостью (построение в программе AutoCAD)](https://i.ytimg.com/vi/vxUMhqndPw8/0.jpg)