 Отрезки и прямые, связанные с окружностью Отрезки и прямые, связанные с окружностью |
 Свойства хорд и дуг окружности Свойства хорд и дуг окружности |
 Теоремы о длинах хорд, касательных и секущих Теоремы о длинах хорд, касательных и секущих |
 Доказательства теорем о длинах хорд, касательных и секущих Доказательства теорем о длинах хорд, касательных и секущих |
 Теорема о бабочке Теорема о бабочке |
- Отрезки и прямые, связанные с окружностью
- Свойства хорд и дуг окружности
- Теоремы о длинах хорд, касательных и секущих
- Доказательства теорем о длинах хорд, касательных и секущих
- Теорема о бабочке
- Что такое хорда окружности в геометрии, её определение и свойства
- Как построить геометрическую хорду
- Свойства
- Взаимосвязь с радиусом и диаметром
- Хорда и радиус
- Отношения со вписанными углами
- Взаимодействия с дугой
- Неверно что . А) хорда окружности , перпендикулярна другой хорде Б) параллельные хорды,проведённые через концы диаметра окружности ,равны В) равные хорды, проведённые через концы диаметра окружности , параллельны
- 🎥 Видео
Видео:Радиус и диаметрСкачать

Отрезки и прямые, связанные с окружностью
| Фигура | Рисунок | Определение и свойства | ||||||||||||||||||||||||||
| Окружность |  | |||||||||||||||||||||||||||
| Круг |  | |||||||||||||||||||||||||||
| Радиус |  | |||||||||||||||||||||||||||
| Хорда |  | |||||||||||||||||||||||||||
| Диаметр |  | |||||||||||||||||||||||||||
| Касательная |  | |||||||||||||||||||||||||||
| Секущая |  | |||||||||||||||||||||||||||
| Окружность |
 |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.
Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.
Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках
Видео:Радиус Хорда ДиаметрСкачать

Свойства хорд и дуг окружности
| Фигура | Рисунок | Свойство |
| Диаметр, перпендикулярный к хорде |  | Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам. |
| Диаметр, проходящий через середину хорды | Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам. | |
| Равные хорды |  | Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности. |
| Хорды, равноудалённые от центра окружности | Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны. | |
| Две хорды разной длины |  | Большая из двух хорд расположена ближе к центру окружности. |
| Равные дуги |  | У равных дуг равны и хорды. |
| Параллельные хорды |  | Дуги, заключённые между параллельными хордами, равны. |
| Диаметр, перпендикулярный к хорде |
 |
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Большая из двух хорд расположена ближе к центру окружности.

У равных дуг равны и хорды.

Дуги, заключённые между параллельными хордами, равны.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Теоремы о длинах хорд, касательных и секущих
| Фигура | Рисунок | Теорема | ||||||||||||||||
| Пересекающиеся хорды |  | |||||||||||||||||
| Касательные, проведённые к окружности из одной точки |  | |||||||||||||||||
| Касательная и секущая, проведённые к окружности из одной точки |  | |||||||||||||||||
| Секущие, проведённые из одной точки вне круга |  | |||||||||||||||||
| Пересекающиеся хорды | ||
 | ||
| Касательные, проведённые к окружности из одной точки | ||
 | ||
| Касательная и секущая, проведённые к окружности из одной точки | ||
 | ||
| Секущие, проведённые из одной точки вне круга | ||
 | ||
| Пересекающиеся хорды |
 |
Произведения длин отрезков, на которые разбита каждая из хорд, равны:
Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.
Видео:№632. Расстояние от точки А до центра окружности меньше радиуса окружности. Докажите, что любаяСкачать

Доказательства теорем о длинах хорд, касательных и секущих
Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).
Тогда справедливо равенство
Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).
Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство
Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).
Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство
Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).
Точка B – точка касания. В силу теоремы 2 справедливы равенства
откуда и вытекает требуемое утверждение.
Видео:Задача 6 №27859 ЕГЭ по математике. Урок 104Скачать

Теорема о бабочке
Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.
Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:
Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим
Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим
Воспользовавшись теоремой 1, получим
Воспользовавшись равенствами (1) и (2), получим
Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство
откуда вытекает равенство
что и завершает доказательство теоремы о бабочке.
Видео:ЕГЭ-2022 ||Задание №6 || Найти длину хордыСкачать

Что такое хорда окружности в геометрии, её определение и свойства
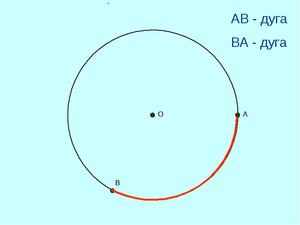
В геометрии для термина определение будет следующим: это отрезок прямой линии, который соединяет между собой две произвольные точки на одной окружности. Если такой отрезок пересекает центр кривой, она называется диаметром описываемой окружности.
Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

Как построить геометрическую хорду
Чтобы построить этот отрезок, прежде всего необходимо начертить круг. Обозначают две произвольные точки, через которые проводят секущую линию. Отрезок прямой, который располагается между точками пересечения с окружностью, называется хордой.
Если разделить такую ось пополам и из этой точки провести перпендикулярную прямую, она будет проходить через центр окружности. Можно провести обратное действие — из центра окружности провести радиус, перпендикулярный хорде. В этом случае радиус разделит её на две идентичные половины.
Если рассматривать части кривой, которые ограничиваются двумя параллельными равными отрезками, то эти кривые тоже будут равными между собой.
Видео:В окружности три хордыСкачать
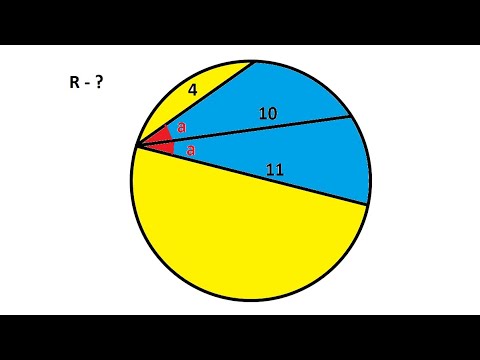
Свойства
Существует ряд закономерностей, связывающих между собой хорды и центр круга:
Если расстояния от хорд до центра равны между собой, то такие хорды тоже равны между собой.
- Существует также обратная зависимость — если длины отрезков равны между собой, то расстояния от них до центра тоже будут равными.
- Чем большую длину имеет стягивающий отрезок прямой, тем меньше расстояние от него до центра окружности. И наоборот, чем она меньше, чем расстояние от указанного отрезка до центра описываемого круга больше.
- Чем больше расстояние от «струны» до центра, тем меньше длина этой оси. Справедливой будет также и обратная взаимосвязь — чем меньше расстояние от центра до хорды, тем больше длина.
- Хорда в геометрии, которая имеет максимально возможную для этой окружности длину, называется диаметром круга. Такая ось проходит через центр и делит её на две равные части.
- Отрезок с наименьшей длиной представляет собой точку.
- Если ось представляет собой точку, то расстояние от неё до центра круга будет равняться радиусу.
Видео:Окружность. Как найти Радиус и ДиаметрСкачать

Взаимосвязь с радиусом и диаметром
Вышеуказанные математические понятия связаны между собой следующими закономерностями:
Если описываемый отрезок не является диаметром этого круга, и этот диаметр делит его пополам, то эта ось и диаметр перпендикулярны между собой.
- С другой стороны, диаметр, который перпендикулярен любой произвольной стягивающей, делит её на две равные части.
- Если ось не является диаметром, и последний делит её на две равные части, то он делит пополам и обе дуги, которые стянуты этим отрезком.
- Если диаметр делит на две одинаковые части дугу, то этот же диаметр делит пополам отрезок, который эту дугу стягивает.
- Если диаметр строго перпендикулярен описываемой величине, то он делит на две половины каждую дугу, которую ограничивает эта линия.
- Если диаметр круга делит пополам отрезок кривой, то он располагается перпендикулярно оси, которая этот отрезок стягивает.
Видео:Вписанный угол, опирающийся на хорду, равную радиусу окружностиСкачать

Хорда и радиус
Между этими понятиями существуют следующие связи:
Если стягивающий отрезок не служит диаметром круга, и радиус разделяет её пополам, то такой радиус является перпендикулярным ей.
- Существует также обратная зависимость — радиус, который перпендикулярен оси, делит её на две одинаковые составные части.
- Если ось не выступает диаметром этого круга, и радиус делит её пополам, то этот же радиус делит пополам и дугу, которая стягивается.
- Радиус, который делит пополам дугу, также делит и отрезок, который эту дугу стягивает.
- Если радиус является перпендикулярным стягивающей линии, то он делит пополам часть кривой, которую она ограничивает.
- Если радиус окружности разделяет на две идентичные части дугу, то он является перпендикулярным линии, которая эту дугу стягивает.
Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Отношения со вписанными углами
Углы, вписанные в окружность, подчиняются следующим правилам:
Если углы, вписанные в окружность, опираются на одну и ту же линию, и их вершины расположены по одну сторону, то такие углы равны между собой.
- Если два вписанных в круг угла опираются на одну и ту же линию, но их вершины расположены по разные стороны этой прямой, то сумма таких углов будет равняться 180 градусам.
- Если два угла — центральный и вписанный — опираются на единую линию, и их вершины располагаются по одну сторону от неё, то величина вписанного угла будет равняться половине центрального.
- Вписанный угол, который опирается на диаметр круга, является прямым.
- Равные между собой по размеру отрезки стягивают равные центральные углы.
- Чем больше величина стягивающего отрезка, тем больше величина центрального угла, который она стягивает. И наоборот, меньшая по размеру линия стягивает меньший центральный угол.
- Чем больше центральный угол, тем больше величина отрезка прямой, который его стягивает.
Видео:Расчет сегмента окружности по хорде и длине цилиндрической поверхности (трансцендентное уравнение)Скачать

Взаимодействия с дугой
Если два отрезка стягивают участки кривой, одинаковые по размеру, то такие оси равны между собой. Из этого правила вытекают следующие закономерности:
Две равные между собой хорды стягивают равные дуги.
- Если рассматривать две дуги, размер которых меньше половины окружности, то чем больше дуга, тем больше хорда, которая будет её стягивать. Напротив, меньшая дуга будет стягиваться меньшей по величине хордой.
- Если же дуга превышает половину окружности, то здесь присутствует обратная закономерность: чем меньше дуга, тем больше хорда, которая её стягивает. И чем больше дуга, тем меньше ограничивающая её хорда.
Хорда, которая стягивает ровно половину окружности, является её диаметром. Если две линии на одной окружности параллельны между собой, то будут равными и дуги, которые заключены между этими отрезками. Однако не следует путать заключённые дуги и стягиваемые теми же линиями.
Видео:№650. Радиус окружности с центром О равен 16. Найдите хорду АВ, если: a) ∠AOB = 60Скачать

Неверно что .
А) хорда окружности , перпендикулярна другой хорде
Б) параллельные хорды,проведённые через концы диаметра окружности ,равны
В) равные хорды, проведённые через концы диаметра окружности , параллельны
2.Неверно , что .
А) из двух неравных хорд хорда большей длины ближе к центру
Б) диаметр окружности есть наибольшая из хорд этой окружности
В) хорда всегда больше радиуса
3.какое утверждение верное?
А) хордой называется отрезок, соединяющий две точки окружности и проходящий через ее центр.
Б)диаметром называется отрезок,проходящий через центр окружности
В) диаметром называется хорда, проходящая через центр
4.верно ли, что.
А) все радиусы одной окружности равны
Б) радиус окружности является ее хордой
В) хорда окружности содержит точно две точки окружности
5.пусть даны две окружности с радиусами R1 и R2 . Каждая из окружностей проходит через центр другой, если
А)R1=R2 ;Б) R1>R2 ;В) R1
6 Верно ли, что
А) расстояния от центра окружности до равных хорд равны
Б) равные хорды параллельны
В) параллельные хорды равны
7 Пусть даны две окружности с радиусами R1 и R2, а расстояние между центрами этих окружностей равно h . Окружности не имеют общих точек, если
А) h=R1+R2 ; Б) h>R1-R2 ; В)R1-R2
🎥 Видео
ОГЭ ЗАДАНИЕ 16 НАЙДИТЕ ДЛИНУ ХОРДЫ ОКРУЖНОСТИ ЕСЛИ РАДИУС 13 РАССТОЯНИЕ ДО ХОРДЫ 5Скачать

Длина хорды окружности равна 72 ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Окружность. 7 класс.Скачать

Радиус описанной окружностиСкачать

Окружность и круг, 6 классСкачать

🌟 ВСЯ ГЕОМЕТРИЯ 🌟 7 класс 🧐ТЕОРЕМЫ 📖ПОВТОРЕНИЕ Треугольники Окружность Секущая Угол Хорда РадиусСкачать

Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать

































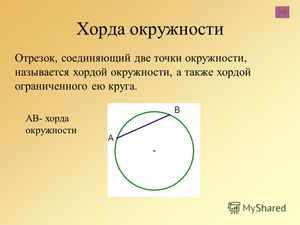 Если расстояния от хорд до центра равны между собой, то такие хорды тоже равны между собой.
Если расстояния от хорд до центра равны между собой, то такие хорды тоже равны между собой.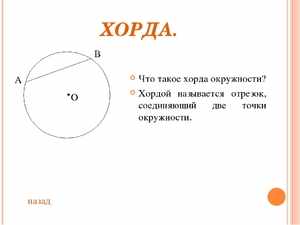 Если описываемый отрезок не является диаметром этого круга, и этот диаметр делит его пополам, то эта ось и диаметр перпендикулярны между собой.
Если описываемый отрезок не является диаметром этого круга, и этот диаметр делит его пополам, то эта ось и диаметр перпендикулярны между собой. Если стягивающий отрезок не служит диаметром круга, и радиус разделяет её пополам, то такой радиус является перпендикулярным ей.
Если стягивающий отрезок не служит диаметром круга, и радиус разделяет её пополам, то такой радиус является перпендикулярным ей.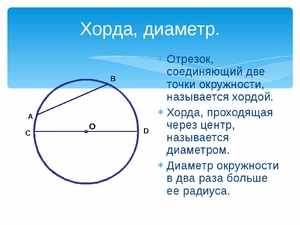 Если углы, вписанные в окружность, опираются на одну и ту же линию, и их вершины расположены по одну сторону, то такие углы равны между собой.
Если углы, вписанные в окружность, опираются на одну и ту же линию, и их вершины расположены по одну сторону, то такие углы равны между собой. Две равные между собой хорды стягивают равные дуги.
Две равные между собой хорды стягивают равные дуги.