Док ва прямоугольного треугольника (8 видео)

Прямоугольный треугольник

Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).

Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.

Стороны, прилежащие к прямому углу, называются катетами .

Содержание

Док ва прямоугольного треугольника
Признаки равенства прямоугольных треугольников
Свойства прямоугольного треугольника
Определение прямоугольного треугольника
Свойства прямоугольного треугольника
Свойство 1
Свойство 2
Свойство 3
Свойство 4
Свойство 5
Пример задачи
📺 Видео

Признаки равенства прямоугольных треугольников

Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и острому углу ).

Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).

Свойства прямоугольного треугольника

1. Сумма острых углов прямоугольного треугольника равна 90˚.

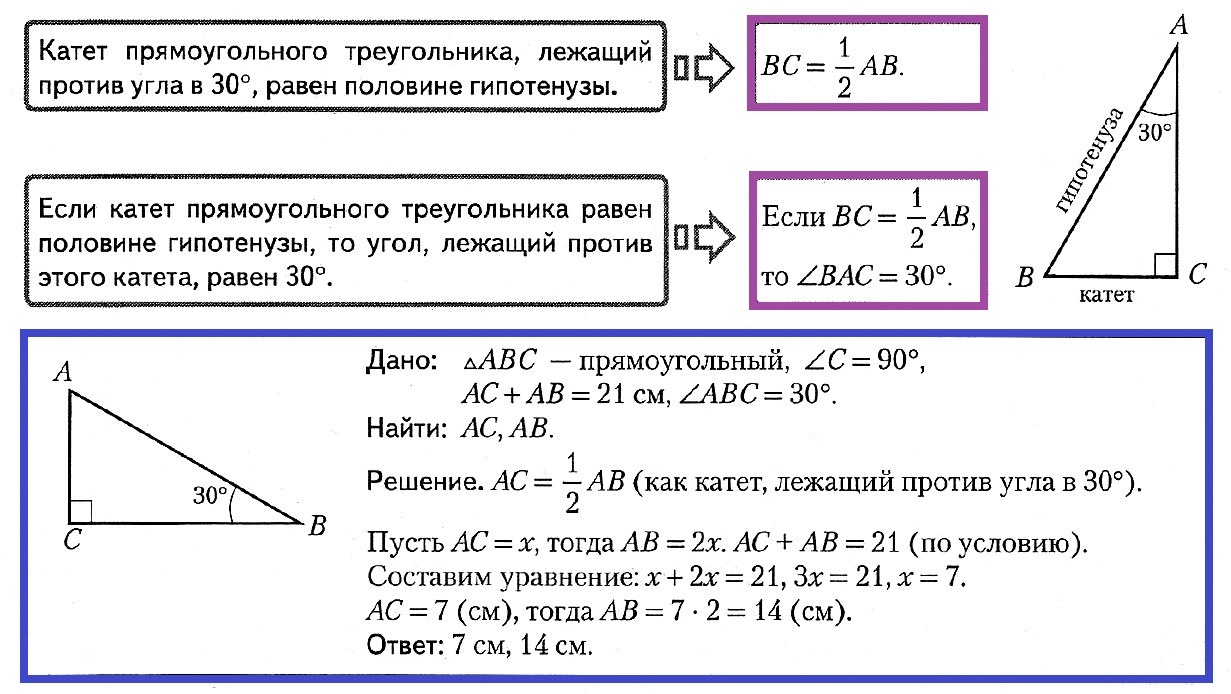
2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.

И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.

3. Теорема Пифагора:

, где – катеты, – гипотенуза. Видеодоказательство

4. Площадь прямоугольного треугольника с катетами :

5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты и гипотенузу следующим образом:

6. Центр описанной окружности – есть середина гипотенузы.

7. Радиус описанной окружности есть половина гипотенузы :

8. Медиана, проведенная к гипотенузе, равна ее половине

9. Радиус вписанной окружности выражается через катеты и гипотенузу следующим образом:

Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Док ва прямоугольного треугольника

Прямоугольный треугольник — треугольник, имеющий прямой угол. Стороны, образующие прямой угол, называют катетами, а сторону, противолежащую к прямому углу, называют гипотенузой.

Свойства прямоугольного треугольника:
1. Катет меньше гипотенузы.
2. Квадрат гипотенузы равен сумме квадратов катетов (теорема Пифагора): с 2 = а 2 + b 2 .
3. Сумма острых углов прямоугольного треугольника равна 90°.
4. Медиана,проведенная к гипотенузе,равна половине гипотенузы (радиусу окружности, описанной около треугольника).
5. Радиус окружности, вписанной в прямоугольный треугольник ,можно вычислить по формуле: r = (a + b — c)/2.
6. Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
7. Если катет прямоугольного треугольника равен 1/2 гипотенузы, то угол, лежащий против этого катета, равен 30°.

Признаки равенства прямоугольных треугольников

Два прямоугольных треугольника равны если:
• два катета одного треугольника равны двум катетам другого;
• катет и острый угол одного треугольника равны катету и острому углу другого треугольника;
• гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу другого треугольника;
• гипотенуза и катет одного треугольника равны гипотенузе и катету другого треугольника.

Это конспект по теме «Прямоугольные треугольники». Выберите дальнейшие действия:

Видео:Свойства прямоугольного треугольника. Практическая часть. 7 класс.Скачать

Свойства прямоугольного треугольника

В данной публикации мы рассмотрим определение и свойства прямоугольного треугольника. Также разберем пример решения задачи для закрепления изложенного материала.

Видео:Свойства прямоугольного треугольника. 7 класс.Скачать

Определение прямоугольного треугольника

Прямоугольным называют треугольник, в котором один из трех углов является прямым, т.е. равным 90°.

Прямоугольный треугольник может быть равнобедренным – когда оба катета равны, а угол между каждым из них и гипотенузой составляет 45°.

Видео:Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Свойства прямоугольного треугольника

Свойство 1

Сумма двух острых углов прямоугольного треугольника равняется 90°.

α + β = 90°

Сумма всех углов любого треугольника составляет 180°. Т.к. один угол равен 90°, на два других, также, остается 90°.

Свойство 2

Катет прямоугольного треугольника, расположенный напротив угла в 30°, равняется половине его гипотенузы.

В нашем случае, катет AB лежит напротив ∠ACB = 30°. Следовательно:

Если длина одного из катетов прямоугольного треугольника в два раза меньше длины его гипотенузы, значит угол напротив этого катета равняется 30°.

Свойство 3

Терему Пифагора можно, также, отнести к свойствам прямоугольного треугольника. Согласно ее формулировке, сумма квадратов катетов (a и b) равняется квадрату гипотенузы (c).

Таким образом, гипотенуза прямоугольного треугольника больше любого из его катетов.

Свойство 4

Медиана, опущенная на гипотенузу прямоугольного треугольника (проведенная из вершины прямого угла), равняется половине гипотенузы.

Свойство 5

Середина гипотенузы прямоугольного треугольника – это центр описанной вокруг него окружности.

Согласно свойству 4, рассмотренному выше, медиана BO равняется половине гипотенузы AC и, одновременно, радиусу окружности, описанной вокруг △ABC.

Видео:Высота в прямоугольном треугольнике. 8 класс.Скачать

Пример задачи

В качестве примера давайте рассмотрим второе свойство, представленное выше. Допустим у нас имеется прямоугольный треугольник ABC с прямым углом в вершине C. Катет BC расположен напротив угла в 30°. Нужно доказать, что BC в два раза меньше гипотенузы AB.

Решение

Нарисуем чертеж по условиям задачи, и зеркально отразим получившийся треугольник.

Получаем △ABD, в котором ∠BAD равен 60° (30° + 30°). Т.к. все три угла данного треугольника равны, он является равносторонним. Следовательно, AD = AB = BD.

Отрезки BC и CD равны между собой (зеркально отраженные), и каждый из них составляет половину BD. Как мы уже выяснили, BD равняется AB.

Таким образом, BC в два раза меньше AB (или AB = 2BC).