| Предмет: | Математика |
| Категория материала: | Другие методич. материалы |
| Автор: | Кобченко Дарья Игоревна это Вы? |
| Тип материала: | Документ Microsoft Word (doc) |
| Размер: | 110.93 Kb |
Полезно? Поделись с другими:
Просмотров: 109 Скачиваний: 47
Если Вы являетесь автором этой работы и хотите отредактировать, либо удалить ее с сайта — свяжитесь, пожалуйста, с нами.
- Посмотрите также:
- Методика обучения учащихся математическим понятиям.
- Просмотр содержимого документа «Методика обучения учащихся математическим понятиям.»
- Логико-дидактический анализ темы Окружность
- «Календарь счастливой жизни: инструменты и механизм работы для достижения своих целей»
- «Управление общеобразовательной организацией: новые тенденции и современные технологии»
- Дистанционное обучение как современный формат преподавания
- Математика: теория и методика преподавания в образовательной организации
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Оставьте свой комментарий
- Подарочные сертификаты
- 📸 Видео
Видео:Переставь одну цифру! Задача на логикуСкачать

Посмотрите также:
Учебно-методические пособия и материалы для учителей, 2015-2020
Все материалы взяты из открытых источников сети Интернет. Все права принадлежат авторам материалов.
По вопросам работы сайта обращайтесь на почту [email protected]
Видео:Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Методика обучения учащихся математическим понятиям.
Просмотр содержимого документа
«Методика обучения учащихся математическим понятиям.»
Выполнить логико-математический анализ понятия: обыкновенная дробь,
неправильная дробь, отрицательное число, биссектриса угла, медиана треугольника, квадратичная функция, окружность:
— выявить вид определения;
— определить структуру определения (каким союзом связаны признаки понятия: и (конъюктивно), или (дизъюктивно));
— раскрыть математическое содержание каждого элемента определения (термин, род, видовые отличия).
— определить объем и содержание понятия.
Определение понятия «обыкновенная дробь»:
Обыкновенные дроби – это записи вида 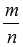
Числителем обыкновенной дроби m/n называется натуральное число m, которое показывает количество взятых равных долей из единого целого. Знаменателем обыкновенной дроби m/n называется натуральное число n, которое показывает, на сколько равных долей разделено единое целое. Обыкновенная дробь дает возможность записывать результат деления двух натуральных чисел, для которых не выполняется деление нацело. Все дробные числа, которые отвечают обыкновенным дробям, можно отобразить на координатном луче. При сравнении двух обыкновенных дробей, если выясняется, что они не равны, можно узнать, какая из них больше, а какая — меньше другой. Для этого используют правило сравнения обыкновенных дробей: нужно привести дроби к общему знаменателю и затем сравнить их числители. У какой дроби числитель будет больше, та дробь и будет являться большей.
Определение понятия «неправильная дробь»:
Неправильная дробь— дробь у которой числитель равен или больше знаменателя. Структура дизъюктивная: признаки соединены союзом «или». Ближайший род-дробь. Видовые отличия: числитель равен знаменателю, числитель больше знаменателя. Объем и содержание понятия: Неправильные дроби используют для описания числа долей. Числитель располагается над дробной чертой, а знаменатель-под дробной чертой.
Числителем неправильной дроби m/n называется натуральное число m, которое показывает количество взятых равных долей из единого целого. Знаменателем неправильной дроби m/n называется натуральное число n, которое показывает, на сколько равных долей разделено единое целое. Неправильная дробь дает возможность записывать результат деления двух натуральных чисел, для которых не выполняется деление нацело.
Определение понятия: «Отрицательное число»:
Отрицательное число-это элемент множества отрицательных чисел, которое (вместе с нулём) появилось в математике при расширении множества натуральных чисел. Ближайший род: натуральное число. Видовые отличия: числа меньше 0, числа со знаком минус. Объем и содержание понятия: любое отрицательное число меньше любого положительного, из двух отрицательных чисел меньше то, что распологается левее на координатной оси, ноль больше любого отрицательного числа. Структура конъюктивная: признаки соеденены союзом «и».
Определение понятия «Биссектриса угла»:
Биссектриса угла: луч с началом в вершине угла, делящий угол на два равных угла. Можно также определить биссектрису как геометрическое место точек внутри угла, равноудалённых от сторон этого угла. Биссектрисой треугольника называется отрезок биссектрисы угла, проведенный от вершины угла до её пересечения с противолежащей стороной. Ближайший род:прямая. Видовые отличия: Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон. Объем и содержание понятия: Точки биссектрисы угла треугольника равноудалены от сторон этого угла. Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности. Также под биссектрисой принято понимать и длину отрезка (что это?), который начинается в вершине треугольника, а заканчивается на противоположной от этой вершины стороне. Есть еще понятие «биссектриса угла», которая является лучом и точно так же делит угол (любой, не обязательно треугольника) пополам. Структура конъюктивная: признаки соеденены союзом «и».
Определение понятия «Медиана треугольника»
Медиана – это отрезок, соединяющий высоту и середину противоположной стороны. В треугольнике три вершины, а значит и медианы три. Медианы не всегда совпадают с высотами или биссектрисами. Чаще всего это отдельные отрезки. Ближайший род: прямая. Видовые отличия: Медиана равнобедренного треугольника, проведенная к основанию, совпадает с высотой и биссектрисой. В равностороннем треугольнике все медианы совпадают с биссектрисами и высотами.
Все медианы треугольника пересекаются в одной точке. Структура конъюктивная: признаки соеденены союзом «и». Объем и содержание понятия: Медиана треугольника делит его на два треугольника равной площади (равновеликих треугольника). Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1, считая от вершины треугольника. Точку пересечения медиан треугольника называют центроидом треугольника. Медианы треугольника делят треугольник на 6 равновеликих треугольников.
Определение понятия «Квадратичная функция»
Функция вида y=ax^2+bx+c, где a не равно 0, b и c – любые числа (они и называются коэффициентами). Число a называют старшим или первым коэффициентом такой функции, b – вторым коэффициентом, а c – свободным членом называется квадратичной функцией. Ближайший род: функции. Структура конъюктивная: признаки соединены союзом «и». Видовые отличия: Графиком квадратичной функции y = x2 является квадратичная парабола. Объем и содержание понятия: Ось y является осью симметрии параболы y = x2 или что парабола симметрична относительно оси y. Ось симметрии как бы разрезает параболу на две части, которые обычно называют ветвями параболы. У параболы есть особая точка, в которой смыкаются обе ветви и которая лежит на оси симметрии параболы — точка (0;0). Данная точка называется вершиной параболы. Свойства функции y = x21) y = 0 при x = 0; y 0 при x 0 и при x 0, то ветви направлены вверх ;если a
Определение понятия «Окружность»
Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая. Ближайший род: замкнутая плоская кривая. Структура конъюктивная: признаки соединены союзом «и». Видовые отличия: Окружностью называют линию, которая ограничивает круг. . Объем и содержание понятия: Окружность имеет центр — это начальная точка нарисования циркулем. Если задуманная точка лежит на окружности, это означает, что она ей принадлежит. Можно обозначить дуги окружности, ими будут любые 2 точки, ограничивающие окружность, т. е. любые две точки A и B окружности разбивают ее на две части; каждая из этих частей и называется дугой. Если провести линию через эти точки, то получим хорду. А хорда, проходящая через центр окружности, имеет название диаметра. Если же от центра провести линии к точке на окружности, то получится радиус окружности.
2. Разработать методику введения данного понятия конкретно-индуктивным методом.
1. Обыкновенная дробь (5 класс).
2. Отрицательные числа (6 класс).
Результат выполнения задания 2 представить в виде таблицы:
Предметные результаты: правильно употреблять в речи определение “обыкновенная дробь” и «отрицательные числа», знать свойства, уметь записывать обыкновенные дроби и отрицательные числа, уметь строить координатную ось и определять на ней положительные, отрицательные, дробные числа, отличать дроби друг от друга по признакам, выполнять правильно необходимые вычислительные действия при решении заданий, решать задания с применением знаний по темам: «Обыкновенные дроби» и «Отрицательные числа»
1. Обыкновенная дробь (5 класс). Цель: ввести определение понятия «обыкновенная дробь» путем конкретного примера.
Метод: частично- поисковый.
Организовывает урок. Отбирает материал для урока. Готовит наглядный материал на тему –«обыкновенные дроби». Ставит познавательные задачи и создает необходимые условия для успешного протекания учения.
(Запишите задачу в тетрадь. Ребята давайте проанализируем все три решенные задачи. Что мы в них находили? Приходим к выводу что нам необходимо число, которое охарактеризует одну или несколько равных частей.
Обьяснение понятия долей.
Выводим существенные признаки:
Содержит одну или несколько равных частей (долей)
Визуализация записи дроби
Число под чертой показывает (знаменует) на сколько равных частей разделили, поэтому под чертой начали называть знаменатель.
Число над чертой показывает сколько таких равных частей взяли. В старину говорили сколько числится , поэтому начали называть числителем. Для закрепления раздает карточки и вместе с учениками подводит итоги.
Слушают задание. Анализируют. Работают самостоятельно и с учителем у доски. Наблюдавю за демонстрациями учителя. Обьясняют наблюдаемое. Отвечают на вопросы и задают вопросы.
Решают задачу: 1)Ребята купили шоколадку разделили ее на 10 равных частей. Саша съел 3 части, а Коля 5 частей. Какую часть шоколадки съел Саша, а какую Коля?
1.На сколько равных частей разделили шоколадку?
2.Сколько съел Саша?
3.Сколько съел Коля?
Ответ:1. на 10 равных частей
2. 3 части из 10 равных
3. 5 частей из 10 равных
Записывают все в рабочие тетради. Отвечают на вопросы.
Выполнение задания по ограничению понятия и подводят итоги.
2.Отрицательные числа(6 класс) Цель: ввести определение понятия «отрицательное число» путем конкретного примера. Чертеж на доске координатной прямой. Вводит понятие «вправо», «влево». Откладывает точки на оси, максимально визиализирует понятие отрицательного числа. Пользуется такими дополнительными средствами визуализации как термометр уличный.Вводит существенные признаки отрицательных чисел. Разбирает понятие на примере задания. Знакомит учащихся со свойствами отрицательных чисел.
Слушают задание. Рассматривают в учебнике пример. Анализируют. Работают самостоятельно и с учителем у доски. Иллюстрируют и записывают все в тетрадь. Наблюдают за демонстрациями учителя. Обьясняют наблюдаемое. Знакомятся со свойствами, признаками отрицательных чисел путем решения заданий. Отвечают на вопросы учителя. Задают вопросы учителю.
В учебнике отдельно дается определение действия сложения чисел с разными знаками, формулировки этих правил содержат указание на следующие действия. В учебнике большое время уделяется к тому как подойти к действию сложению. Основное внимание уделяется к рассмотрению конкретных задач, обращаясь при этом к координатной прямой. Подводят итоги.
Видео:КАК РАЗОБРАТЬСЯ В ВЫСШЕЙ МАТЕМАТИКЕСкачать

Логико-дидактический анализ темы Окружность
Видео:Матан. Пределы для успешной сдачи зачёта | TutorOnline МатематикаСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»
Сертификат и скидка на обучение каждому участнику
КОНТРОЛЬНАЯ РАБОТА № 1
Составить логико-дидактический анализ одной из тем из курса алгебры 7–9 классов, указанных ниже, по следующему плану:
Место темы в курсе математики.
Пропедевтика изучения темы.
Методическое планирование темы.
Схема формирования основных понятий.
Изложение темы в различных учебниках.
Изучение темы в спецклассах (по желанию. ).
Различные формы контроля при изучении данной темы (математический диктант, самостоятельная работа, тест, модульная работа).
Конспект одного из уроков темы.
Методическое планирование темы
(обязательно указать учебник. )
Материал для мотивации
Геометрия — важнейшая ступень в дальнейшем изучении практических задач. Она делиться на два крупнейших раздела- планиметрия и стрериометрия. Планиметрия это наука которая изучает фигуры на плоскости. Тема окружность часть планиметрии. Изучается в 8м классе.
2. В теме окружности будут доказаны различные теоремы , которые связаны с окружностью в том числе теоремы об окружностях вписанных в треугольник, четырехугольник, окружностях описанных около этих фигур. Кроме того будут доказаны три утверждения о замечательных точках треугольника-точки пересечения биссектрис треугольника, точки пересечении высот и точки пересечения серединных перпендикуляров к сторонам треугольника.
ТЕМА 4. Окружность
Взаимное расположение прямой и окружности
Касательная к окружности.
Градусная мера дуги окружности
Теорема о вписанном угле.
Теорема об отрезках пересекающихся хорд.
Решение задач по теме «Центральные и вписанные углы»
Свойство биссектрисы угла.
Теорема о точке пересечения высот треугольника
Свойство описанного четырехугольника.
Свойство вписанного четырехугольника.
Окружность. Контрольная работа № 5.
Методическое планирование темы
(Геометрия 7-9, Атанасян)
Материал для мотивации
Взаимное расположение прямой и окружности
Рассмотреть различные случаи взаимного расположения прямой и окружности.
Ввести понятия касательной, точке касания.
Рассмотреть свойство касательной.
Повторить теорию о треугольниках
Проверка выполнений заданий на доске
Плакат с окружностью
Создать вместе с детьми модель окужности
Касательная к окружности
ввести понятие касательной, точки касания,
Повторить понятье окружности
Проверка индивидуально тетрадей
Стенды с окружностью
С помощью макета окружности, создать макет касательной
Касательная к окружности
рассмотреть свойство касательной и её признак и показать их применение при решении задач в природе и технике.
Повторить определения касательная к окружности
Задача с дидактического задачника
Контроль методом обмена тетрадей
Презентация «Касательная к окружности»
Градусная мера дуги окружности
ввести понятие градусной меры дуги окружности, центрального угла;
Повторить определения касательная к окружности
Проверка выполнений заданий на доске
Теорема о вписанном угле
ввести понятие вписанного угла;
рассмотреть теорему о вписанном угле и следствия из нее;
Повторить определения градусной меры дуги
Проверка индивидуально тетрадей
Теорема об отрезках
познакомиться с теоремой об отрезках пересекающихся хорд и сформировать навыки по её применению для решения задач .
Контроль методом обмена тетрадей
Решение задач по теме «Центральные и вписанные углы»
Развитие способностей анализировать, проводить сопоставление, обобщать, строить доказательства, проводить наблюдения, планировать деятельность.
Воспитание культуры речи; построение плана ответа; формирование умений осуществлять взаимоконтроль.
Проверка выполнений заданий на доске
Свойство биссектрисы угла
Рассмотреть теорему о свойстве биссектрисы угла и её следствие.
Учить применять данные теоремы и следствие при решении задач.
Формировать умения применять известные знания в незнакомой ситуации, сравнивать, анализировать, обобщать.
Контроль методом обмена тетрадей
Доказать теорему о пересечении высот треугольника или их продолжения. Закрепить знание формулировок теорем о свойстве биссектрисы угла и серединного перпендикуляра к отрезку и следствий из этих теорем
Задача с дидактического задачника
Контроль методом обмена тетрадей
Теорема о точке пересечения высот треугольника
Рассмотреть теорему о точке пересечения высот и следствие из неё;
Формировать умения применять известные знания в незнакомой ситуации, сравнивать, анализировать, обобщать
Задача с дидактического задачника
Задача с дидактического задачника
Проверка выполнений заданий на доске
ввести для учащихся определение вписанной окружности, сформировать представление о свойствах вписанной окружности, теореме и способе ее доказательства; научить учащихся применять данные знания при решении задач
Задача с дидактического задачника
Проверка индивидуально тетрадей
Свойство описанного четырехугольника.
Создание условий для успешного усвоения понятия описанного четырёхугольника, его свойства, признака и овладения умениями применять их на практике.
Проверка выполнений заданий на доске
систематизировать теоретический материал;
совершенствовать навыки решения задач.
Свойство вписанного четырехугольника.
Продолжить знакомство учащихся со свойствами вписанных четырехугольников, доказать теорему Птолемея, рассмотреть решения задач на свойства вписанных в четырехугольники и описанных около четырехугольников окружностей.
Задача с дидактического задачника
Задача с дидактического задачника
Проверка индивидуально тетрадей
Продолжить знакомство учащихся со свойствами вписанных четырехугольников, доказать теорему Птолемея, рассмотреть решения задач на свойства вписанных в четырехугольники и описанных около четырехугольников окружностей.
Задача с дидактического задачника
Задача с дидактического задачника
Задача с дидактического задачника
Проверка выполнений заданий на доске
Окружность. Контрольная работа № 5.
4 Схема формирований понятий
Окружность – две общее точки окружности – одна точка окужности –касательная к окружности — полуокружность – вписанный угол –дуга –замечатьные точки треугольника – вписанная окружность – описанная окружность .
Видео:Математический анализ. Алексей Савватеев и Александр Тонис. Лекция 4.1. Предел - основа мат.анализаСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 931 человек из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 702 человека из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 333 человека из 72 регионов
Ищем педагогов в команду «Инфоурок»
- Кобченко Дарья ИгоревнаНаписать 1478 03.03.2017
Номер материала: ДБ-241762
- 03.03.2017 673
- 03.03.2017 537
- 03.03.2017 181
- 03.03.2017 205
- 03.03.2017 402
Не нашли то, что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Более половины россиян сталкиваются с конфликтами в родительских чатах
Время чтения: 2 минуты
Проходной балл ЕГЭ для поступления на бюджет снизился впервые за 10 лет
Время чтения: 3 минуты
В России ежегодно будут обучать плаванию не менее 500 тыс. детей
Время чтения: 2 минуты
В Подмосковье вводят систему голосования оценки качества школьных столовых
Время чтения: 1 минута
Утвержден список федеральных инновационных площадок в образовании на 2022 год
Время чтения: 1 минута
В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
📸 Видео
Математический анализ. Алексей Савватеев и Александр Тонис. Лекция 1.1. Как далеко видно с горыСкачать
Отюцкий Г.П. принимает логикуСкачать

Шаталов за одну минуту доказывает теорему, на которую традиционно выделяется 45 минут урока!Скачать

ВВЕДЕНИЕ В МАТАНАЛИЗ — АЛЕКСЕЙ САВВАТЕЕВСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Самая сложная задача из самой сложной олимпиады [3Blue1Brown]Скачать
![Самая сложная задача из самой сложной олимпиады [3Blue1Brown]](https://i.ytimg.com/vi/S6_R5j8hzbY/0.jpg)
Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

10. Конечные подгруппы движений прямой и окружности. Алексей Савватеев. 100 уроков математикиСкачать

Математический анализ. Алексей Савватеев и Александр Тонис. Лекция 2.3. Аксиома полнотыСкачать

Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать






