Линия которая делит треугольник пополам (6 видео)

Замечательные линии треугольника

Содержание

Медиана
Свойства медиан треугольника
Биссектриса
Свойства биссектрис треугольника
Высота
Свойства высот треугольника
Срединный перпендикуляр
Свойства серединных перпендикуляров треугольника
Средняя линия
Свойство средней линии треугольника
Линия которая делит треугольник пополам
Треугольник
📽️ Видео

Видео:Средняя линия треугольника и трапеции. 8 класс.Скачать

Медиана

Медиана треугольника – это отрезок, который связывает вершину треугольника с серединой одной из сторон данного треугольника.

Видео:Геометрия. Линии в треугольникеСкачать

Свойства медиан треугольника

Медиана делит треугольник на два треугольника, площади которых одинаковы.

Медианы треугольника пересекаются только в одной точке, которая разделяет каждую из них в отношении 2 : 1 , отсчитывая от вершины. Такая точка именуется центром тяжести треугольника.

Весь треугольник разбивается своими медианами на шесть равных по значению треугольников.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Биссектриса

Биссектриса угла – это исходящий из вершины угла луч, пролегающий между образующими сторонами и разделяющий его пополам.

Видео:Средняя линия. Теорема о средней линии треугольникаСкачать

Свойства биссектрис треугольника

Свойства биссектрисы треугольника

Биссектриса угла – есть геометрическое место точек, которые равноудалены от сторон этого угла.

Биссектриса угла треугольника, разделяет противолежащую сторону на отдельные отрезки, которые пропорциональны прилежащим сторонам:

В точке, где пересекаются биссектрисы треугольника, находится центр окружности, который вписан в этот треугольник.

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Высота

Высотой треугольника называется линия, проведенная из вершины треугольника к одной из сторон расположенной перпендикулярно.

Видео:Точка пересечения медиан в треугольникеСкачать

Свойства высот треугольника

Свойства высоты треугольника

Перпендикулярная линия высоты прямоугольного треугольника разделяет его на два подобных ему треугольника.

Две линии высоты остроугольного треугольника, отделяют от него подобные треугольники.

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Срединный перпендикуляр

Перпендикулярная прямая, которая проходит через середину отрезка, называется – срединный перпендикуляр к отрезку.

Видео:Средняя линия треугольникаСкачать

Свойства серединных перпендикуляров треугольника

Все точки серединного перпендикуляра к отрезку равноудалены от окончаний этого отрезка. Верно так же и обратное утверждение, что каждая точка, находящаяся на равных расстояниях от концов отрезка, расположена на серединном перпендикуляре к нему.

В точке пересечения серединных перпендикуляров, проведенных в направлении к одной из сторон треугольника, находится центр окружности, который описывает данный треугольник.

Видео:64. Средняя линия треугольникаСкачать

Средняя линия

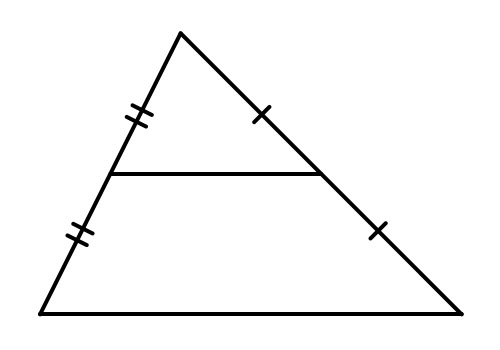
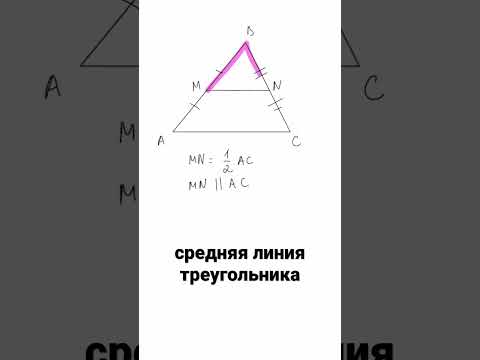
Отрезок, который соединяет две стороны треугольника в их серединах, называется – средняя линия треугольника.

Видео:СРЕДНЯЯ ЛИНИЯ ТРЕУГОЛЬНИКА 8 класс Атанасян геометрияСкачать

Свойство средней линии треугольника

Средняя линия, какого либо треугольника, всегда расположена параллельно одной из его сторон и является половиной этой стороны.

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Линия которая делит треугольник пополам

Ключевые слова: основные линии треугольника, медиана, биссектриса, высота, средния линия, серединные перпендикуляры

Рассмотрим произвольный треугольник ABC:

a, b, c — стороны треугольника

$$m_a$$ — медиана к стороне a угла A

$$h_a$$ — высота к стороне a угла A

$$l_a$$ — биссектриса к стороне a угла A

Медиана треугольника — это отрезок, соединяющий верщину треугольника с серединой противолежащей стороны этого треугольника.

Свойства медиан треугольника

Медиана разбивает треугольник на два треугольника одинаковой площади.
Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.
Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.

Биссектриса угла — это луч, который исходит из его вершины, проходит между его сторонами и делит данный угол пополам.
Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.

Свойства биссектрис треугольника

Биссектриса угла — это геометрическое место точек, равноудаленных от сторон этого угла.
Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилегажащим сторонам.
Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник.

Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника.

Свойства высот треугольника

В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному.
В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.
Если треугольник остроугольный, то все основания высот принадлежат сторонам треугольника, а у тупоугольного треугольника две высоты попадают на продолжение сторон
Три высоты в остроугольном треугольнике пересекаются в одной точке и эту точку называют ортоцентром треугольника.

Свойства серединных перпендикуляров треугольника

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Свойство средней линии треугольника

Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

Видео:Средняя линия треугольника — Геометрия ОГЭСкачать

Треугольник

Рис. 1. Треугольник (общий случай)

Треугольник — замкнутая геометрическая фигура, состоящая из трёх отрезков (в общем случае, разных). В физике эти отрезки классически называются буквами латинского алфавита ( и т.д.), в отличие от обозначений в геометрии.

Итак, треугольник, у которого все стороны имеют разную длину и ни один из углов не равен , называется произвольным (рис. 1).

В случае, если у треугольника равны две стороны, данный треугольник называется равнобедренным.

В случае, если у треугольника все стороны одинаковы, он называется равносторонним.

В случае, если у треугольника один и углов прямой ( ), он называется прямоугольным.

Для произвольного треугольника вводят ряд отрезков, характеризующих треугольник и обладающих собственными свойствами:

Для разных типов треугольников поиск длин параметров треугольника может происходить по-разному. Для физических задач использование конкретной формулы диктуется конкретными данными задачи.

Рис. 2. Треугольник (биссектриса)

Биссектриса угла — геометрическое место точек, равноудалённых от сторон этого угла. Т.е. биссектриса — это линия, которая делит угол треугольника пополам (рис. 2). Известно, что биссектриса внутреннего угла треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам.

Для нахождения биссектрисы угла через различные данные можно пользоваться следующими соотношениями:

Медиана треугольника — отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны. Все медианы треугольника пересекаются в одной точке: данная точка делит медианы в соотношении 2 к 1, считая от вершины (рис. 3).