Биссектриса треугольника делит треугольник пополам

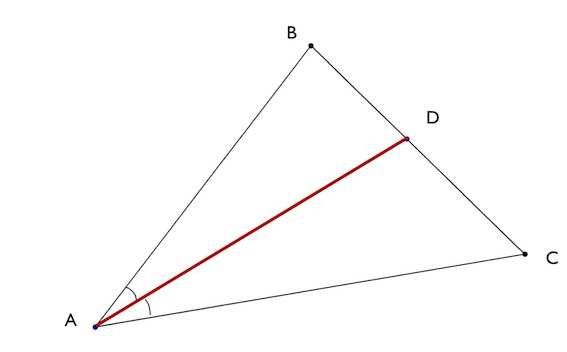
Теорема 1. Биссектриса при вершине треугольника делит противоположную сторону на две отрезки, пропорциональные сторонам, прилежащим к данной вершине. То есть если биссектриса при вершине A делит в точке D сторону BC на отрезки BD и CD (Рис.1), то имеет место следующее соотношение:

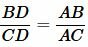(1)

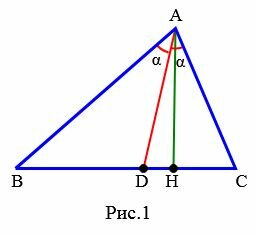Доказательство (метод площадей 1). Из вершины A опущена биссектриса AD. Построим вершину треугольника AH. Найдем площади треугольников ABD и ACD:

,

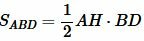(3)

.

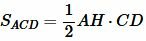(4)

Построим следующее соотношение

.

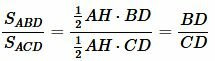(5)

С другой стороны, площадь треугольников ABD и ACD можно найти используя следующие формулы:

.

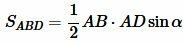(6)

.

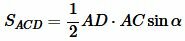(7)

Построим следующее соотношение используя формулы (6) и (7):

.

(8)

Из формул (5) и (8) получим соотношение (1).

Доказательство (метод площадей 2). С одной стороны, аналогично вышеизложенному имеем соотношение (5). Далее из точки D проведем вершины L и M для треугольников ABD и ACD (Рис.2).

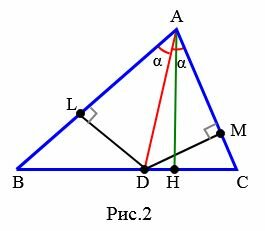Тогда площади треугольников ABD и ACD можно найти из формул:

,

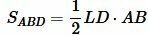(9)

.

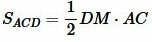(10)

Построим следующее соотношение

.

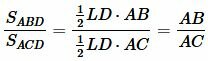(11)

Из формул (5) и (11) получим соотношение (1).

Доказательство (через теорему синусов). Рассмотрим треугольник ABC. Из точки A проведем биссектрису AD (Рис.3):

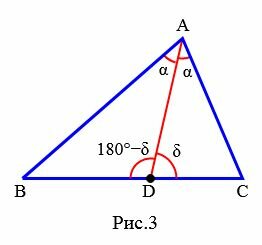Применяя теорему синусов для треугольников ABD и ACD можем записать:

,

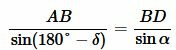(12)

.

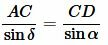(13)

Поделив (12) на (13) и учитывая, что ( small sin(180°-delta)=sin delta , ) (см. статью Формулы приведения тригонометрических функций онлайн) получим равенство (1).

Доказательство (через подобие треугольников). Рассмотрим треугольник ABC. Из точки A проведем биссектрису AD (Рис.4). Проведем перпендикуляры из вершин B и C на луч AD и обозначим точки пересечения через L и K.

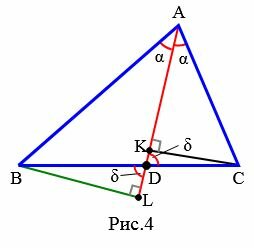Рассмотрим треугольники ABL и ACK. Эти треугольники подобны по двум углам (( small ∠ ALB= ∠ AKC ,;; ∠ BAL= ∠ CAK ) ). Тогда имеем:

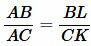(14)

Рассмотрим, далее, треугольники BLD и CKD. Они также подобны поскольку ( small ∠ BLD= ∠ CKD ,) а углы BDL и CDK равны так как они вертикальные. Тогда имеет место следующее соотношение:

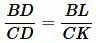(15)

Из равенств (14) и (15) получаем:

.

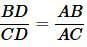Пример. Даны стороны треугольника ABC: AB=18, AC=6, BC=20. Найти отрезки, полученные делением биссектрисей большой стороны треугольника.

Решение. Поскольку напротив самой большой стороны треугольника находится вершина A, то бисскетриса AD делит сторону BC на отрезки BD и CD. Тогда имеем:

.

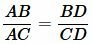(16)

Обозначим BD=x. Тогда CD=BC−x=20−x. Подставляя данные в уравнение (16), получим:

.

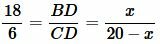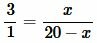(17)

Методом перекресного умножения упростим (17) и решим:

Видео:3 свойства биссектрисы #shortsСкачать

Биссектриса треугольника делит треугольник пополам

Какое из следующих утверждений верно?

1) Отношение площадей подобных треугольников равно коэффициенту подобия.

2) Диагонали прямоугольника точкой пересечения делятся пополам.

3) Биссектриса треугольника делит пополам сторону, к которой она проведена.

В ответе запишите номер выбранного утверждения.

1) Отношение площадей подобных треугольников равно коэффициенту подобия. — неверно, отношение площадей равно квадрату коэффициента подобия.

2) Диагонали прямоугольника точкой пересечения делятся пополам. — верно, из свойства диагоналей прямоугольника.

3)Биссектриса треугольника делит пополам сторону, к которой она проведена. — неверно, биссектриса делит угол, из которого выходит, на два равных угла.

Видео:Биссектриса треугольника делит пополам сторону ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Элементы треугольника. Биссектриса

Биссектриса треугольника – отрезок биссектрисы угла треугольника, заключенный между вершиной треугольника и противолежащей ей стороной.

Видео:Свойство биссектрисы треугольника с доказательствомСкачать

Свойства биссектрисы

1. Биссектриса треугольника делит угол пополам.

2. Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон ()

3. Точки биссектрисы угла треугольника равноудалены от сторон этого угла.

4. Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности.

Видео:Запоминаем: высота, медиана биссектриса треугольникаСкачать

Некоторые формулы, связанные с биссектрисой треугольника

(доказательство формулы – здесь)
, где
— длина биссектрисы, проведённой к стороне ,
— стороны треугольника против вершин соответственно,
— длины отрезков, на которые биссектриса делит сторону ,

Приглашаю посмотреть видеоурок, в котором демонстрируется применение всех указанных выше свойств биссектрисы.

Задачи, рассматриваемые в видеоролике:
1.В треугольнике АВС со сторонами АВ=2 см, ВС=3 см, АС=3 см проведена биссектриса ВМ. Найти длины отрезков АМ и МС
2. Биссектриса внутреннего угла при вершине А и биссектриса внешнего угла при вершине С треугольника АВС пересекаются в точке М. Найдите угол BMC, если угол В равен 40, угол С – 80 градусов
3. Найти радиус окружности, вписанной в треугольник, считая стороны квадратных клеток равными 1

Возможно, вам будет интересен и этот небольшой видеоурок, где применяется одно из свойств биссектрисы

Чтобы не потерять страничку, вы можете сохранить ее у себя:

🌟 Видео

Биссектриса прямого угла делит медиану пополам! Найти площадь треугольника.Скачать

№535. Докажите, что биссектриса треугольника делит противоположную сторону на отрезки,Скачать

Биссектрисы треугольника.Скачать

Высота, биссектриса, медиана. 7 класс.Скачать

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Формула для биссектрисы треугольникаСкачать

Геометрия В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину ВСкачать

Построение биссектрисы угла. 7 класс.Скачать

Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

ПОСТРОЕНИЕ БИССЕКТРИСЫ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Cекретное свойство биссектрисыСкачать

Секретная формула биссектрисы треугольника плюс Задача из экзамена 9 классСкачать

11 класс, 46 урок, Теорема о биссектрисе треугольникаСкачать

Свойства биссектрисы треугольникаСкачать

Как построить биссектрису, медиану и высоту в треугольникеСкачать

Биссектриса треугольника. Построение. 1 частьСкачать