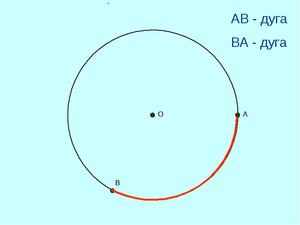
В геометрии для термина определение будет следующим: это отрезок прямой линии, который соединяет между собой две произвольные точки на одной окружности. Если такой отрезок пересекает центр кривой, она называется диаметром описываемой окружности.
Видео:Вписанная окружность делит чевиану пополам. ЗАДАЧА - БЛЕСК!Скачать

Как построить геометрическую хорду
Чтобы построить этот отрезок, прежде всего необходимо начертить круг. Обозначают две произвольные точки, через которые проводят секущую линию. Отрезок прямой, который располагается между точками пересечения с окружностью, называется хордой.
Если разделить такую ось пополам и из этой точки провести перпендикулярную прямую, она будет проходить через центр окружности. Можно провести обратное действие — из центра окружности провести радиус, перпендикулярный хорде. В этом случае радиус разделит её на две идентичные половины.
Если рассматривать части кривой, которые ограничиваются двумя параллельными равными отрезками, то эти кривые тоже будут равными между собой.
Видео:На окружности по разные стороны от диаметра AB ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Свойства
Существует ряд закономерностей, связывающих между собой хорды и центр круга:
Если расстояния от хорд до центра равны между собой, то такие хорды тоже равны между собой.
- Существует также обратная зависимость — если длины отрезков равны между собой, то расстояния от них до центра тоже будут равными.
- Чем большую длину имеет стягивающий отрезок прямой, тем меньше расстояние от него до центра окружности. И наоборот, чем она меньше, чем расстояние от указанного отрезка до центра описываемого круга больше.
- Чем больше расстояние от «струны» до центра, тем меньше длина этой оси. Справедливой будет также и обратная взаимосвязь — чем меньше расстояние от центра до хорды, тем больше длина.
- Хорда в геометрии, которая имеет максимально возможную для этой окружности длину, называется диаметром круга. Такая ось проходит через центр и делит её на две равные части.
- Отрезок с наименьшей длиной представляет собой точку.
- Если ось представляет собой точку, то расстояние от неё до центра круга будет равняться радиусу.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Взаимосвязь с радиусом и диаметром
Вышеуказанные математические понятия связаны между собой следующими закономерностями:
Если описываемый отрезок не является диаметром этого круга, и этот диаметр делит его пополам, то эта ось и диаметр перпендикулярны между собой.
- С другой стороны, диаметр, который перпендикулярен любой произвольной стягивающей, делит её на две равные части.
- Если ось не является диаметром, и последний делит её на две равные части, то он делит пополам и обе дуги, которые стянуты этим отрезком.
- Если диаметр делит на две одинаковые части дугу, то этот же диаметр делит пополам отрезок, который эту дугу стягивает.
- Если диаметр строго перпендикулярен описываемой величине, то он делит на две половины каждую дугу, которую ограничивает эта линия.
- Если диаметр круга делит пополам отрезок кривой, то он располагается перпендикулярно оси, которая этот отрезок стягивает.
Видео:Теорема о диаметре, перпендикулярном хордеСкачать

Хорда и радиус
Между этими понятиями существуют следующие связи:
Если стягивающий отрезок не служит диаметром круга, и радиус разделяет её пополам, то такой радиус является перпендикулярным ей.
- Существует также обратная зависимость — радиус, который перпендикулярен оси, делит её на две одинаковые составные части.
- Если ось не выступает диаметром этого круга, и радиус делит её пополам, то этот же радиус делит пополам и дугу, которая стягивается.
- Радиус, который делит пополам дугу, также делит и отрезок, который эту дугу стягивает.
- Если радиус является перпендикулярным стягивающей линии, то он делит пополам часть кривой, которую она ограничивает.
- Если радиус окружности разделяет на две идентичные части дугу, то он является перпендикулярным линии, которая эту дугу стягивает.
Видео:#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

Отношения со вписанными углами
Углы, вписанные в окружность, подчиняются следующим правилам:
Если углы, вписанные в окружность, опираются на одну и ту же линию, и их вершины расположены по одну сторону, то такие углы равны между собой.
- Если два вписанных в круг угла опираются на одну и ту же линию, но их вершины расположены по разные стороны этой прямой, то сумма таких углов будет равняться 180 градусам.
- Если два угла — центральный и вписанный — опираются на единую линию, и их вершины располагаются по одну сторону от неё, то величина вписанного угла будет равняться половине центрального.
- Вписанный угол, который опирается на диаметр круга, является прямым.
- Равные между собой по размеру отрезки стягивают равные центральные углы.
- Чем больше величина стягивающего отрезка, тем больше величина центрального угла, который она стягивает. И наоборот, меньшая по размеру линия стягивает меньший центральный угол.
- Чем больше центральный угол, тем больше величина отрезка прямой, который его стягивает.
Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Взаимодействия с дугой
Если два отрезка стягивают участки кривой, одинаковые по размеру, то такие оси равны между собой. Из этого правила вытекают следующие закономерности:
Две равные между собой хорды стягивают равные дуги.
- Если рассматривать две дуги, размер которых меньше половины окружности, то чем больше дуга, тем больше хорда, которая будет её стягивать. Напротив, меньшая дуга будет стягиваться меньшей по величине хордой.
- Если же дуга превышает половину окружности, то здесь присутствует обратная закономерность: чем меньше дуга, тем больше хорда, которая её стягивает. И чем больше дуга, тем меньше ограничивающая её хорда.
Хорда, которая стягивает ровно половину окружности, является её диаметром. Если две линии на одной окружности параллельны между собой, то будут равными и дуги, которые заключены между этими отрезками. Однако не следует путать заключённые дуги и стягиваемые теми же линиями.
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Линия, делящая круг пополам
Ответ на кроссворд из 7 букв, на букву Д:
Видео:Делим окружность НА 5 РАВНЫХ ЧАСТЕЙСкачать

ДИАМЕТР
Что значит слово ДИАМЕТР в словарях:
- «Дважды радиус»
- «Калибр» круга
- В два раза больше радиуса
- Главное отличие сосиски от сардельки
- Два радиуса
- Два радиуса — один за одним
- Два радиуса на одной линии
- Двойной радиус
- Делит круг на половинки
- Делит круг пополам
- Делит окружность пополам
- Итог сложения двух радиусов
- Вопрос: Линия, делящая круг пополам — ответ: ДИАМЕТР
- Максимальная из хорд
- Математический калибр
- Отрезок прямой, соединяющий две точки окружности, проходящий через центр
- Отрезок, соединяющий две точки окружности и проходящий через её центр
- Радиус плюс радиус
- Радиус, переходящий в радиус
- Рубит круг пополам
- Самая длинная хорда
- Самый длинный мост через окружность
- Талия круга
- Толщина круглоты
- У всех советских сигарет он был равен 7, 62 мм
- У дискеты он составлял 3,5 дюйма
- Удвоенный радиус
- Хорда через центр
- мера круга
- поперечник круга
Линия, что делит квадрат наискосок
Видео:Круг. Окружность (центр, радиус, диаметр)Скачать

Линия, делящая круг пополам.
Добрый вечер! Здравствуйте, уважаемые дамы и господа! Пятница! В эфире капитал-шоу «Поле чудес»! И как обычно, под аплодисменты зрительного зала я приглашаю в студию тройку игроков. А вот и задание на этот тур:
Вопрос: Линия, делящая круг пополам. (Слово из 7 букв)
Если этот ответ не подходит, пожалуйста воспользуйтесь формой поиска.
Постараемся найти среди 775 682 формулировок по 141 989 словам .
💡 Видео
Окружность и все, что нужно про нее знать. ТеорияСкачать

[10] Окружности с нуля для ЕГЭ по математике. Линия центров перпендикулярна общей хорде и делит...Скачать
![[10] Окружности с нуля для ЕГЭ по математике. Линия центров перпендикулярна общей хорде и делит...](https://i.ytimg.com/vi/OuPstDE05CQ/0.jpg)
Окружность, диаметр, хорда геометрия 7 классСкачать

Деление окружностей на равные частиСкачать
Математика 3 класс (Урок№33 - Круг. Окружность (центр, радиус, диаметр)Скачать

Построение окружности по трём точкам.Скачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Теорема о числе точек пересечения двух окружностейСкачать

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Точка, прямая и отрезок. 1 часть. 7 класс.Скачать

Отрезок, луч, прямаяСкачать

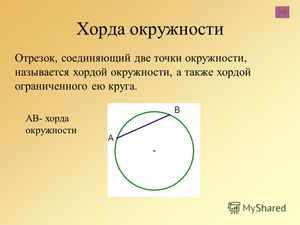 Если расстояния от хорд до центра равны между собой, то такие хорды тоже равны между собой.
Если расстояния от хорд до центра равны между собой, то такие хорды тоже равны между собой.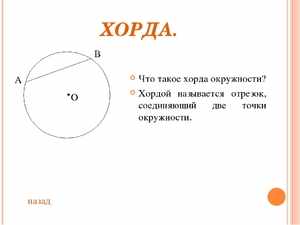 Если описываемый отрезок не является диаметром этого круга, и этот диаметр делит его пополам, то эта ось и диаметр перпендикулярны между собой.
Если описываемый отрезок не является диаметром этого круга, и этот диаметр делит его пополам, то эта ось и диаметр перпендикулярны между собой. Если стягивающий отрезок не служит диаметром круга, и радиус разделяет её пополам, то такой радиус является перпендикулярным ей.
Если стягивающий отрезок не служит диаметром круга, и радиус разделяет её пополам, то такой радиус является перпендикулярным ей.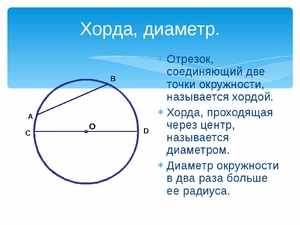 Если углы, вписанные в окружность, опираются на одну и ту же линию, и их вершины расположены по одну сторону, то такие углы равны между собой.
Если углы, вписанные в окружность, опираются на одну и ту же линию, и их вершины расположены по одну сторону, то такие углы равны между собой.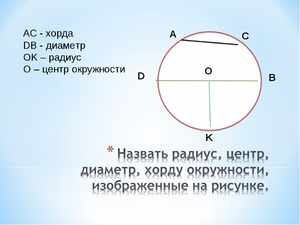 Две равные между собой хорды стягивают равные дуги.
Две равные между собой хорды стягивают равные дуги.