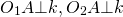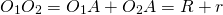Говорят, что две окружности касаются, если они имеют единственную общую точку. Эта точка называется точкой касания окружностей. Касание окружностей бывает внутренним и внешним.
- Внутреннее касание
- Внешнее касание
- Окружности касаются внутренним образом рисунок
- Две окружности на плоскости. Общие касательные к двум окружностям
- Взаимное расположение двух окружностей
- Формулы для длин общих касательных и общей хорды двух окружностей
- Доказательства формул для длин общих касательных и общей хорды двух окружностей
- Касание двух окружностей
- Касание окружностей
- Внутреннее касание
- Внешнее касание
- Выбери соответствующие рисунку утверждения.
- 🌟 Видео
Видео:Геометрия Две окружности касаются внутренним образом в точке A, причем меньшая окружность проходитСкачать

Внутреннее касание
Касание называется внутренним, если центры окружностей лежат по одну сторону от точки касания окружностей. Построим две окружности, первая с центром A и радиусом AC, отметим на радиусе AC точку B, это будет центр второй окружности с радиусом BC:
Построенные окружности имеют только одну общую точку C. Говорят, что они касаются внутренним образом.
При внутреннем касании двух окружностей, расстояние между их центрами равно разности их радиусов.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Внешнее касание
Касание называется внешним, если центры окружностей лежат по разные стороны от точки касания. Построим две окружности, первая с центром A и радиусом AC, вторая с центром B и радиусом BC:
Построенные окружности имеют только одну общую точку C. Говорят, что они касаются внешним образом.
При внешнем касании двух окружностей, расстояние между их центрами равно сумме их радиусов.
Видео:Задача. Две окружности касаются внутренним образом.Скачать

Окружности касаются внутренним образом рисунок
Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Две окружности на плоскости.
Общие касательные к двум окружностям
 Взаимное расположение двух окружностей Взаимное расположение двух окружностей |
 Общие касательные к двум окружностям Общие касательные к двум окружностям |
 Формулы для длин общих касательных и общей хорды Формулы для длин общих касательных и общей хорды |
 Доказательства формул для длин общих касательных и общей хорды Доказательства формул для длин общих касательных и общей хорды |
Видео:Задача №16. Пересекающиеся и касающиеся окружности.Скачать

Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |  |
Взаимное расположение на плоскости двух окружностей радиусов r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей

Расстояние между центрами окружностей больше суммы их радиусов

Расстояние между центрами окружностей равно сумме их радиусов

Расстояние между центрами окружностей равно разности их радиусов

Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов
r1 – r2 лежит внутри другой

Расстояние между центрами окружностей меньше разности их радиусов
d r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей

Расстояние между центрами окружностей больше суммы их радиусов

Расстояние между центрами окружностей равно сумме их радиусов

Расстояние между центрами окружностей равно разности их радиусов

Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов
r1 – r2 лежит внутри другой

Расстояние между центрами окружностей меньше разности их радиусов
d r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей

Расстояние между центрами окружностей больше суммы их радиусов

Расстояние между центрами окружностей равно сумме их радиусов
Расстояние между центрами окружностей равно разности их радиусов

Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов
r1 – r2 лежит внутри другой
Расстояние между центрами окружностей меньше разности их радиусов
d внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.

Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.

Существует единственная общая внешняя касательная. Других общих касательных нет.

Существуют две общих внешних касательных. Других общих касательных нет.

Существует единственная общая внутренняя касательная, а также
две общих внешних касательных. Других общих касательных нет.

Каждая из окружностей лежит вне другой
Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет

| Внешняя касательная к двум окружностям | |
 | |
| Внутренняя касательная к двум окружностям | |
 | |
| Внутреннее касание двух окружностей | |
 | |
| Окружности пересекаются в двух точках | |
 | |
| Внешнее касание двух окружностей | |
 | |
 | |
| Каждая из окружностей лежит вне другой | |
 | |
| Внешняя касательная к двум окружностям | ||||||||||||||
| Внутренняя касательная к двум окружностям | ||||||||||||||
| Внутреннее касание двух окружностей | ||||||||||||||
| Окружности пересекаются в двух точках | ||||||||||||||
| Внешнее касание двух окружностей | ||||||||||||||
| Каждая из окружностей лежит вне другой | ||||||||||||||
| Фигура | Рисунок | Формула |
| Внешняя касательная к двум окружностям |  |
Длина общей внешней касательной к двум окружностям вычисляется по формуле

Длина общей внутренней касательной к двум окружностям вычисляется по формуле

Длина общей хорды двух окружностей вычисляется по формуле
| Внешняя касательная к двум окружностям | ||||
 | ||||
| Внутренняя касательная к двум окружностям | ||||
 | ||||
| Общая хорда двух пересекающихся окружностей | ||||
 | ||||
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Общая хорда двух пересекающихся окружностей |
 Длина общей хорды двух окружностей вычисляется по формуле Видео:Все Задания 8 ЕГЭ 2024 ПРОФИЛЬ из Банка ФИПИ (Математика Школа Пифагора)Скачать  Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, Видео:Задание 24 Две пересекающиеся окружностиСкачать 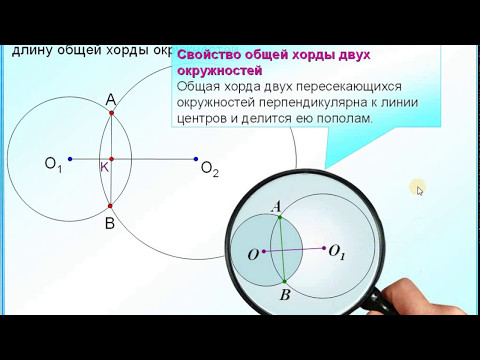 Касание двух окружностейДве окружности, имеющие общую точку, касаются в этой точке, если они имеют в ней общую касательную. Общая точка двух окружностей называется точкой касания окружностей. Касание окружностей может быть внешним и внутренним. Внешнее касание окружностей — это касание, при котором центры окружностей лежат по разные стороны от общей касательной. Внутреннее касание окружностей — касание, при котором центры окружностей лежат по одну сторону от общей касательной. Касающиеся окружности имеют только одну общую точку — точку касания. Центры касающихся окружностей и их общая точка касания лежат на одной прямой. При любом виде касания по свойству касательной касательная перпендикулярна радиусам, проведённым в точку касания: По теореме о существовании и единственности прямой, перпендикулярной данной,через точку A можно провести только одну прямую, перпендикулярную данной прямой k. Следовательно, все три точки: центры окружностей O1, O2 и A лежат на одной прямой. Что и требовалось доказать . При внешнем касании расстояние между центрами окружностей равно сумме их радиусов: При внутреннем касании расстояние между центрами окружностей равно разности радиусов: Видео:4.3. Вписанные и описанные окружности. Вневписанные окружности.Скачать  Касание окружностейГоворят, что две окружности касаются, если они имеют единственную общую точку. Эта точка называется точкой касания окружностей. Касание окружностей бывает внутренним и внешним. Видео:ОГЭ № 25. "Окружности касаются внешним образом... "Скачать  Внутреннее касаниеКасание называется внутренним, если центры окружностей лежат по одну сторону от точки касания окружностей. Построим две окружности, первая с центром A и радиусом AC, отметим на радиусе AC точку B, это будет центр второй окружности с радиусом BC: Построенные окружности имеют только одну общую точку C. Говорят, что они касаются внутренним образом. При внутреннем касании двух окружностей, расстояние между их центрами равно разности их радиусов. Видео:✓ Всё, что нужно знать про окружность | ЕГЭ. Задания 1 и 16. Профильный уровень | Борис ТрушинСкачать  Внешнее касаниеКасание называется внешним, если центры окружностей лежат по разные стороны от точки касания. Построим две окружности, первая с центром A и радиусом AC, вторая с центром B и радиусом BC: Построенные окружности имеют только одну общую точку C. Говорят, что они касаются внешним образом. При внешнем касании двух окружностей, расстояние между их центрами равно сумме их радиусов. Видео:1 2 4 сопряжение окружностейСкачать  Выбери соответствующие рисунку утверждения.1.Окружности касаются внутренне. 2.У окружностей имеется одна общая точка, внутреннее касание. 4.Окружности касаются внешне. 5.У окружностей имеются две общие точки. 6.У окружностей нет общих точек, одна окружность находится за пределами другой. 7.У окружностей имеется одна общая точка, внешнее касание. 8.У окружностей нет общих точек, одна окружность расположена внутри другой. 🌟 ВидеоКасательные к окружностиСкачать  Окружность №16 из ОГЭ. Свойства хорд, касательных, секущих.Скачать  Черчение. Внутреннее, внешнее и смешенное сопряжение двух окружностей.Скачать  Уравнение окружности (1)Скачать  Решение планиметрических задач повышенного уровня сложностиСкачать  ОГЭ Задание 26 Внешнее касание двух окружностейСкачать  Длина окружности. Математика 6 класс.Скачать  Окружности, связанные с треугольником и четырёхугольникомСкачать  |